电压、电流和电阻之间的关系
当一个导电的路径被创造出来允许自由电子连续移动时,电路就形成了。这种自由电子在电路导体中的连续运动称为现在的,它通常被称为“流”,就像液体流过空心管道一样。
促使电子在电路中“流动”的力叫做电压. 电压是一种势能的具体量度,在两点之间总是相对的。当我们谈到电路中存在一定量的电压时,我们指的是对电压的测量潜在的能量的存在使电子从电路中的一个特定点移动到另一个特定点。未提及二特别是,术语“电压”没有意义。
自由电子倾向于在有一定摩擦或运动阻力的导体中移动。这种反对动议的说法更恰当抵抗. 电路中的电流大小取决于激励电子的电压大小,以及电路中阻止电子流动的电阻大小。就像电压一样,电阻是两点之间的相对量。因此,电压和电阻的量通常被称为电路中两点之间的或交叉的。
为了能够对电路中的这些量做出有意义的陈述,我们需要能够用我们可以量化质量、温度、体积、长度或任何其他物理量的方式来描述它们的量。质量可以用“千克”或“克”来表示,温度可以用华氏度或摄氏度来表示。以下是电流、电压和电阻的标准测量单位:

给每个量的“符号”是在代数方程中用来表示该量的标准字母。像这样的标准化字母在物理和工程学科中很常见,并且是国际公认的。每个量的“单位缩写”代表字母符号,用作其特定计量单位的速记符号。是的,那个奇怪的“马蹄铁”符号是希腊大写字母Ω,只是a中的一个字符外国的字母表(向所有希腊读者致歉)。
每种测量单位都是以一位著名的电学实验者的名字命名的放大器在法国人安德烈·安培之后伏特在意大利人亚历山德罗·沃尔塔之后ohm在德国人格奥尔格·西蒙·奥姆之后。
每个数量的数学符号也是有意义的。电阻的“R”和电压的“V”都是不言而喻的,而电流的“I”似乎有点奇怪。“I”被认为是用来表示“强度”(电子流),另一个电压符号“E”代表“电动势”。根据我所做的研究,似乎对“I”的含义存在一些争议。“E”和“V”在很大程度上是可互换的,尽管有些文本保留了“E”来表示源(如电池或发电机)的电压,而“V”则表示其他任何电源之间的电压。
所有这些符号都是用大写字母表示的,除非用短时间(称为“瞬时”值)来描述一个量(尤其是电压或电流)。例如,长期稳定的电池电压将用大写字母“E”表示,“而闪电击中电线瞬间的电压峰值很可能用小写字母“e”(或小写“v”)表示该值在某一时刻出现。同样的小写约定也适用于current,小写字母“i”代表某个时刻的current。然而,大多数直流(DC)测量值随着时间的推移而稳定,将用大写字母表示。
电子学单元的基础课程通常在课程开始时才被教授,但后来很少使用库仑,它是一种电荷量,与不平衡状态下的电子数成正比。一库仑电荷等于625000000000000电子。电荷量的符号是大写字母“Q”,库仑单位由大写字母“C”缩写。因此,电子流的单位安培等于1秒内通过电路中某个给定点的1库仑电子。在这些术语中,current是电荷运动速率通过导体
如前所述,电压是单位电荷势能可以激发电子从一点到另一点。在我们能够精确地定义什么是“伏特”之前,我们必须了解如何测量这个我们称之为“势能”的量焦耳,等于1牛顿的力通过1米的运动(同一方向)所做的功。以英制单位计算,这略小于1英尺距离上施加的力的3/4磅。一般来说,把一个3/4磅重的物体抬离地面1英尺,或者用3/4磅的平行拉力将物体拖离1英尺的距离,大约需要1焦耳的能量。在这些科学术语中,1伏特等于每1库仑电荷1焦耳的电势。因此,一个9伏的电池每经过一个电路就释放出9焦耳的能量。
当我们开始探索电路中它们之间的关系时,这些表示电量的单位和符号将变得非常重要。第一个,也许是最重要的,电流、电压和电阻之间的关系被称为欧姆定律,由格奥尔格·西蒙·欧姆发现并发表在他1827年的论文中,电流电路的数学研究. 欧姆的主要发现是,在任何给定的温度下,通过电路中金属导体的电流量与施加在其上的电压成正比。Ohm用一个简单的方程式表达了他的发现,描述了电压、电流和电阻之间的相互关系:
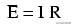
在这个代数表达式中,电压(E)等于电流(I)乘以电阻(R)。利用代数技术,我们可以将该方程转化为两个变量,分别求解I和R:

让我们看看这些方程式如何帮助我们分析简单电路:
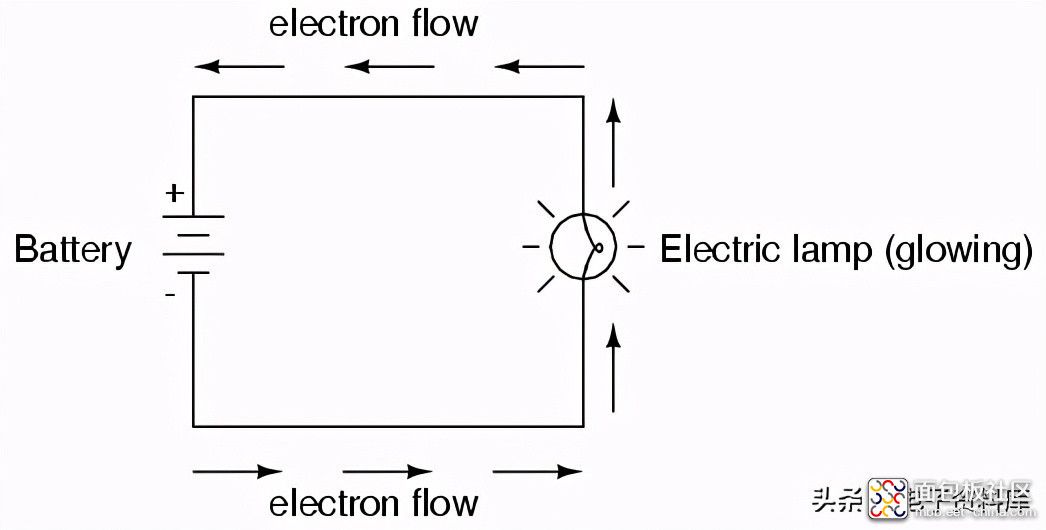
在上述电路中,只有一个电压源(左侧的蓄电池)和一个电流电阻源(右侧的灯)。这使得欧姆定律的应用变得非常容易。如果我们知道电路中三个量(电压、电流和电阻)中任何两个的值,我们就可以用欧姆定律来确定第三个量。
在第一个例子中,我们将计算电路中的电流(I),给定电压(E)和电阻(R):
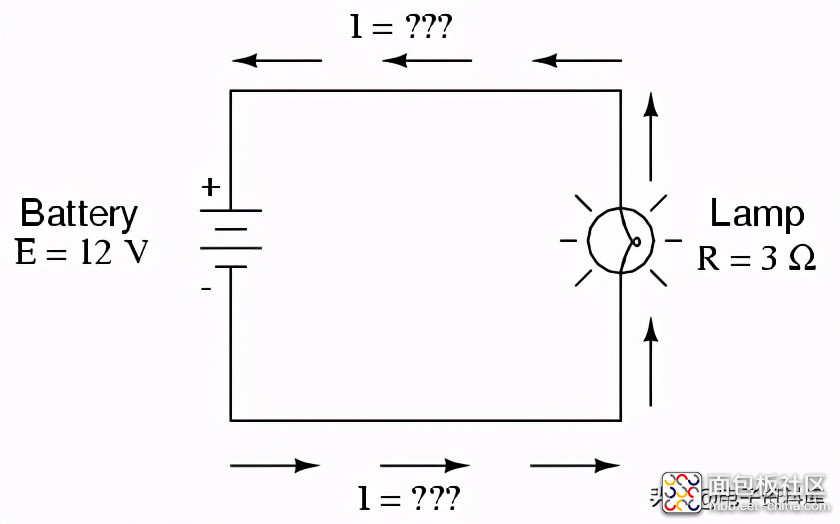
这个电路的电流(I)是多少?
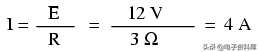
在第二个例子中,我们将计算电路中的电阻(R),给定电压(E)和电流(I):
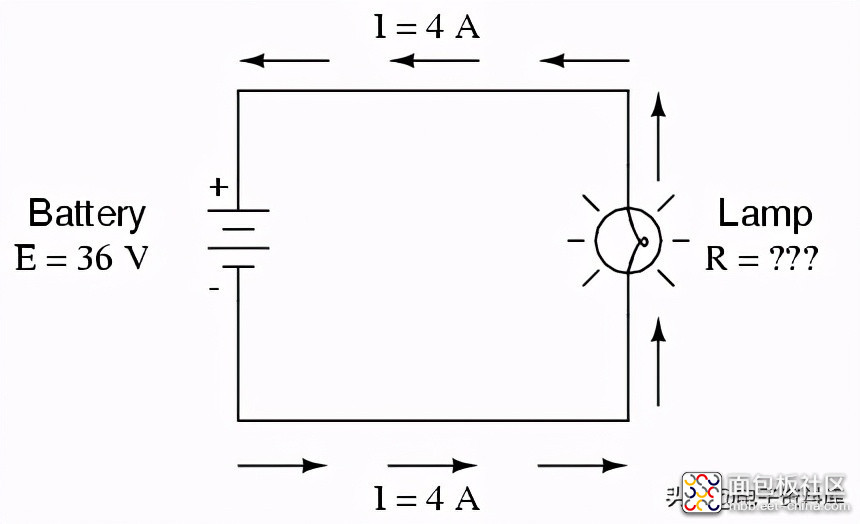
灯提供的电阻(R)是多少?
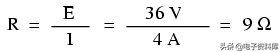
最后,我们将计算电池供电的电流值(以a为例):
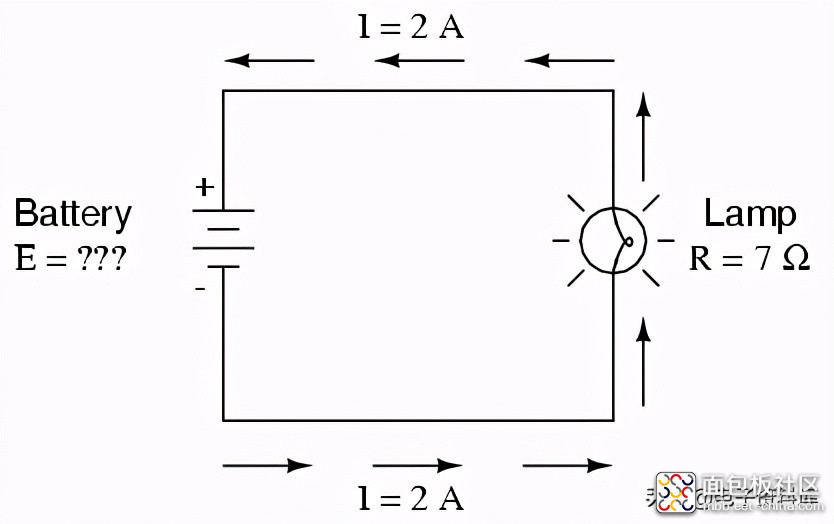
电池的电压是多少?
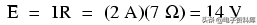
欧姆定律是分析电路的一个非常简单和有用的工具。电学和电子学的学习中经常用到它,所以认真学习的学生必须记住它。对于那些还不熟悉代数的人来说,有一个诀窍就是记住如何解决任何一个量,而另两个量。首先,将字母E、I和R排列成三角形,如下所示:
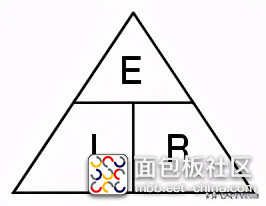
如果您知道E和I,并且希望确定R,只需从图中消除R,然后看看剩下的是什么:
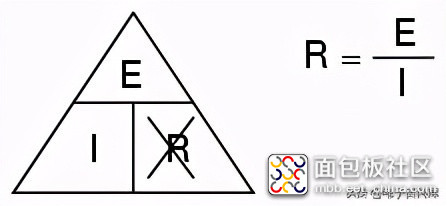
如果你知道E和R,想确定I,去掉I,看看剩下的是什么:
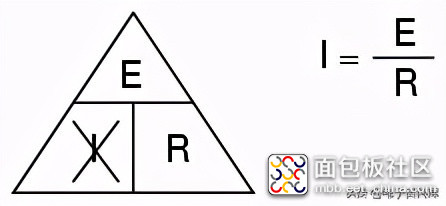
最后,如果您知道I和R,并希望确定E,则消除E,然后看看剩下的是什么:
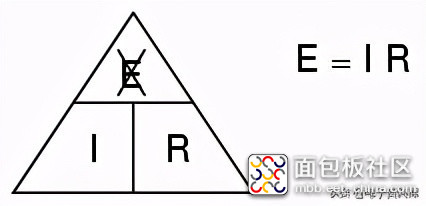
Eventually, you'll have to be familiar with algebra to seriously study electricity and electronics, but this tip can make your first calculations a little easier to remember. If you are comfortable with algebra, all you need to do is commit E=IR to memory and derive the other two formulae from that when you need them!
- 回顾:
- 电压测量单位volts,用字母“E”或“V”表示。
- 电流测量单位安培,以字母“I”为象征。
- 电阻测量单位欧姆,以字母“R”表示
- Ohm's Law: E = IR ; I = E/R ; R = E/I
欧姆定律的类比
如果你把欧姆定律应用到水和管道的类比中,它也有直观的意义。如果我们有一个水泵,它施加压力(电压)使水通过一个限制(电阻)在“电路”(电流)中流动,我们就可以模拟这三个变量之间的相互关系。如果水流阻力保持不变,泵压力增加,流速也必须增加。
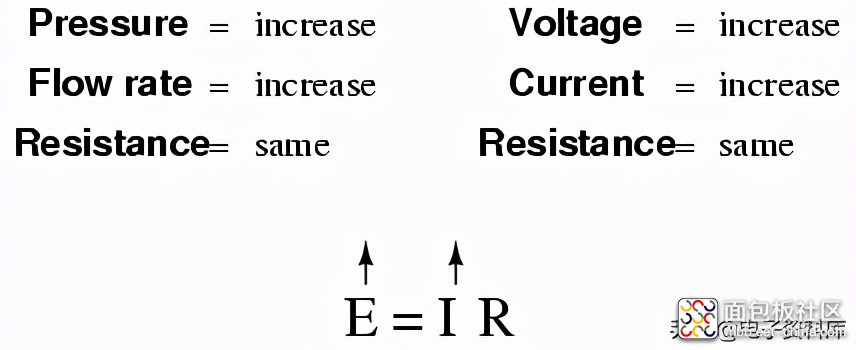
如果压力保持不变且阻力增大(使水更难流动),则流速必须降低:
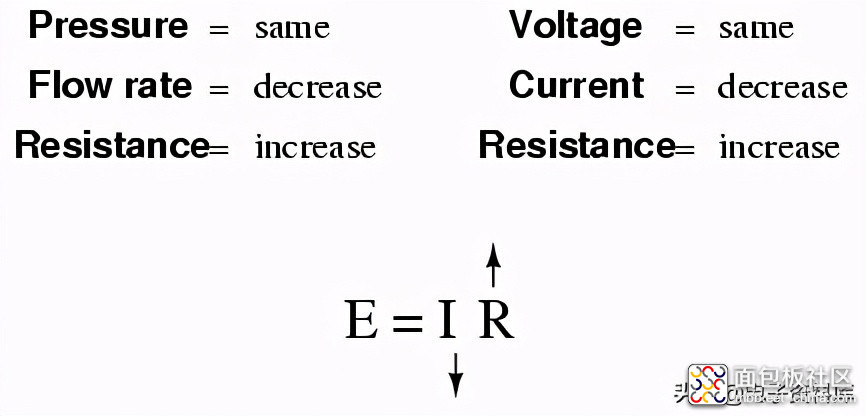
如果流量保持不变,而流动阻力减小,则所需的泵压力将必然降低:

尽管看起来很奇怪,但对于像水这样的流体来说,压力、流量和阻力之间的实际数学关系实际上比电子更复杂。如果你继续深造物理学,你会发现这一点的。感谢电子专业的学生,欧姆定律的数学非常简单明了。
- 回顾:
- 在电阻稳定的情况下,电流跟随电压(电压的增加意味着电流的增加,反之亦然)。
- 电压稳定时,电流和电阻的变化是相反的(电流增加意味着电阻减小,反之亦然)。
- 当电流稳定时,电压跟随电阻(电阻的增加意味着电压的增加)。
电路中的功率
除了电压和电流外,还有另一种测量电路中自由电子活动的方法:权力. 首先,在分析任何电路中的功率之前,我们需要了解它到底是什么。
功率是在给定的时间内可以完成多少工作的度量。工作通常是指在重力的作用下提升重物。重量越重和/或提升得越高,所做的工作就越多。权力是衡量标准工作量完成的速度。
美国制造业者发明的一种“马力发动机”最初被称为“马力的发动机”,这是他们发明的最常用的马力单位。一马力用英国单位定义为每秒550英尺磅的功。汽车发动机的功率并不能说明它能爬多高的山,也不能显示它能牵引多少重量,但它能显示出它能爬多高快速的它可以爬上一个特定的山或拖一个特定的重量。
机械发动机的功率是发动机转速和输出轴扭矩的函数。发动机输出轴的转速以每分钟转数或每分钟转数来衡量。扭矩是发动机产生的扭转力的大小,通常用磅-英尺或磅-英尺(不要与英尺-磅或英尺-磅混淆,这是功的单位)。无论是转速还是扭矩都不能单独衡量发动机的功率。
100马力的柴油拖拉机发动机转动相对较慢,但提供了很大的扭矩。一个100马力的摩托车发动机会转得很快,但提供的扭矩相对较小。两者都将产生100马力,但在不同的速度和扭矩。轴功率的方程式很简单:

注意等式右侧只有两个变量项,S和T。另一侧的所有其他项都是常量:2、pi和33000都是常量(它们的值不变)。马力只随转速和扭矩的变化而变化,其他都没有。我们可以重新编写方程来显示这种关系:
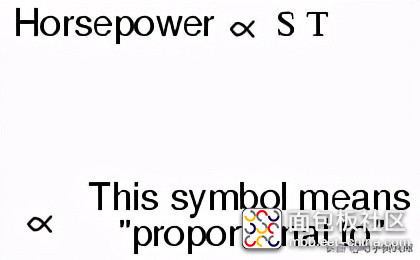
因为“马力”的单位与转速(每分钟转数)乘以扭矩(磅-英尺)并不完全一致,所以我们不能说马力等于不过,他们是圣成比例的彼此之间。当ST的数学积改变时,马力的值也会以同样的比例变化。
在电路中,功率是电压和电流的函数。毫不奇怪,这种关系与上面的“比例”马力公式惊人地相似:
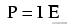
然而,在这种情况下,功率(P)正好等于电流(I)乘以电压(E),而不仅仅是与IE成比例。使用此公式时,功率的测量单位是瓦特,缩写为字母“W”
必须明白,电压和电流本身都不构成功率。相反,功率是两种电压的组合和电路中的电流。记住电压是单位电荷的比功(或势能),而电流是电荷通过导体的速率。电压(比功)类似于在重力作用下提升重物所做的功。电流(速率)类似于重量提升的速度。与电压(a)乘积(a)共同构成功。
与柴油拖拉机发动机和摩托车发动机的情况一样,高电压和低电流电路消耗的功率可能与低压大电流电路相同。无论是单独的电压量还是单独的电流量都不能说明电路中的功率大小。
在开路中,如果电源端子之间存在电压且电流为零,则零不管电压有多大,能量都会消散。因为P=IE和I=0,任何乘以0的东西都是0,所以在任何开路中耗散的功率都必须是0。同样地,如果我们有一个由超导导线组成的回路(绝对零电阻)构成的短路,我们可以在回路中有一个电流为零电压的条件,同样地,没有电能被耗散。因为P=IE,E=0,任何乘以0的东西都是0,超导回路中耗散的功率必须是0。(我们将在下一章探讨超导性的话题)。
无论我们用“马力”还是“瓦特”来衡量功率,我们谈论的仍然是同一件事:在给定的时间内可以完成多少功。这两个单位在数字上不相等,但它们表达的是同一种东西。事实上,欧洲汽车制造商通常以千瓦(kW)或数千瓦特来宣传他们的发动机功率,而不是马力!这两个功率单位通过一个简单的换算公式相互关联:
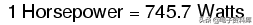
因此,我们的100马力柴油机和摩托车发动机也可以被评为“74570瓦”发动机,或者更准确地说,是“74.57千瓦”发动机。在欧洲工程规范中,这一评级将是规范而不是例外。
- 回顾:
- 功率是衡量在一定时间内能完成多少工作的量度。
- 机械功率(在美国)通常用“马力”来衡量
- Electrical power is almost always measured in "watts," and it can be calculated by the formula P = IE.
- 电能是两种电压的乘积和现在,不是单独一个
- 马力和瓦特只是描述同一种物理测量的两种不同单位,1马力等于745.7瓦。
计算电力
我们已经看到了确定电路中功率的公式:通过将电压(单位为伏特)乘以电流(单位为安培),我们就得到了以“瓦特”为单位的答案
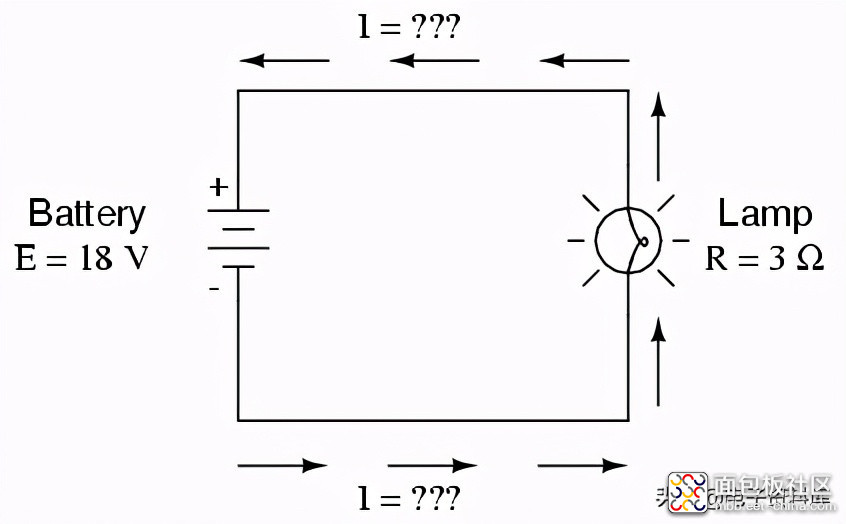
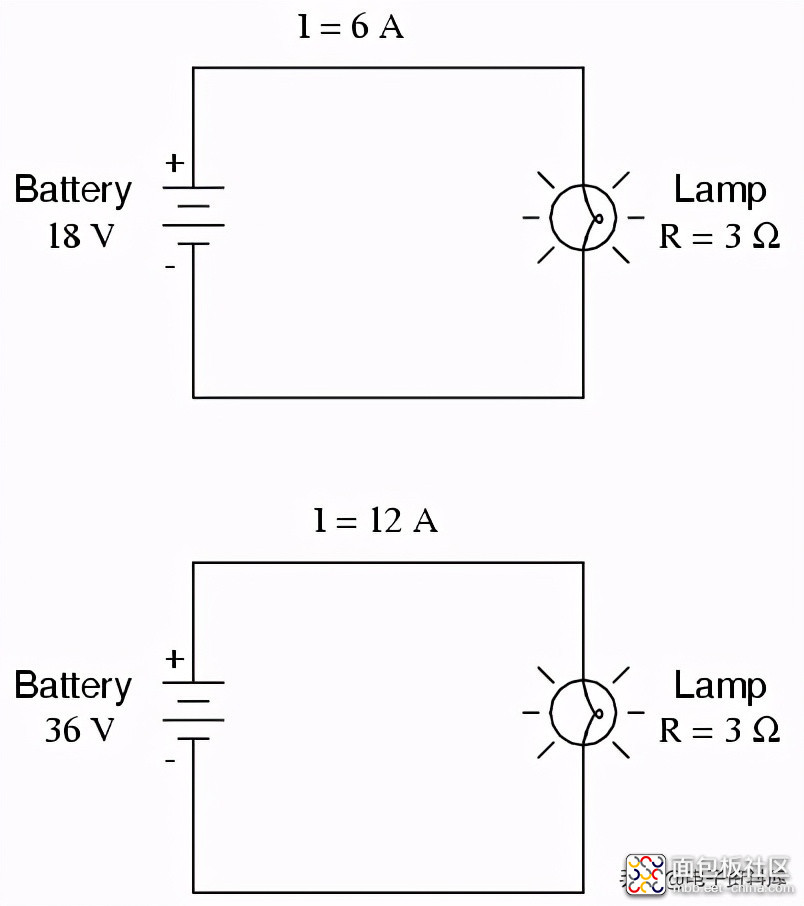
在上面的电路中,我们知道我们的电池电压是18伏,灯的电阻是3Ω。利用欧姆定律确定电流,我们得到:
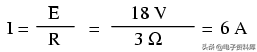
现在我们知道了电流,我们可以取这个值乘以电压来确定功率:
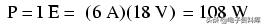
答:这盏灯正在消耗(释放)108瓦的功率,很可能是以光和热的形式。
让我们试着用同样的电路增加电池电压看看会发生什么。直觉应该告诉我们,电路电流会随着电压的增加而增加,而灯的电阻保持不变。同样,功率也会增加:
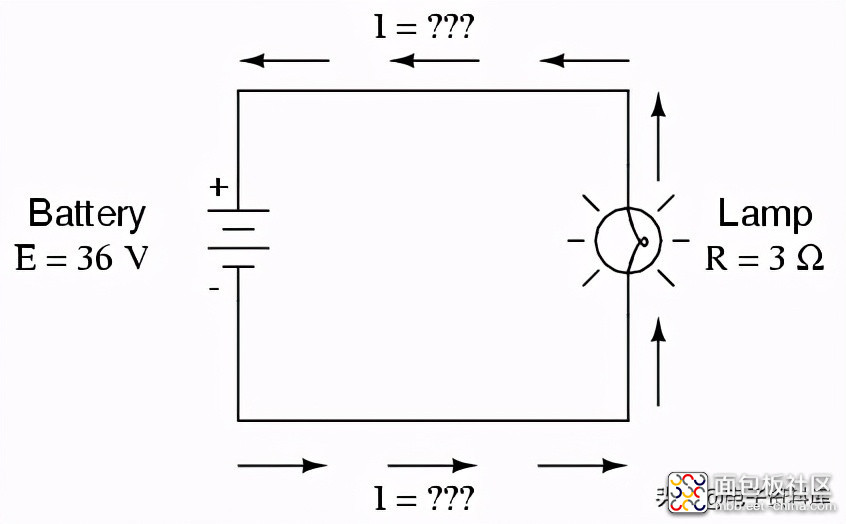
现在,电池电压是36伏,而不是18伏。灯仍然为电子流提供3Ω的电阻。现在是:
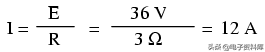
这是有道理的:如果I=E/R,我们把E加倍,而R保持不变,电流应该加倍。事实上,它有:我们现在有12安培的电流而不是6安培。那么,功率呢?
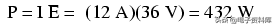
注意,功率增加了,正如我们所怀疑的,但是它比电流增加了很多。为什么会这样?因为功率是电压乘以电流的函数二者都电压和电流比之前的值翻了一番,功率将增加2×2或4倍。你可以用432瓦特除以108瓦特来检查,看看它们之间的比率确实是4。
再次使用代数来操作公式,我们可以采用原来的功率公式并对其进行修改,以便在不知道电压和电流的情况下:
如果我们知道电阻(R):
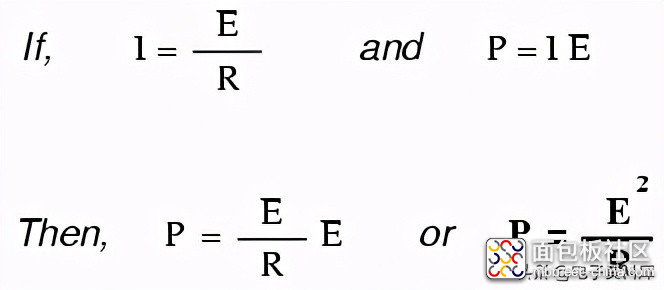
如果我们只知道电流(I)和电阻(R):
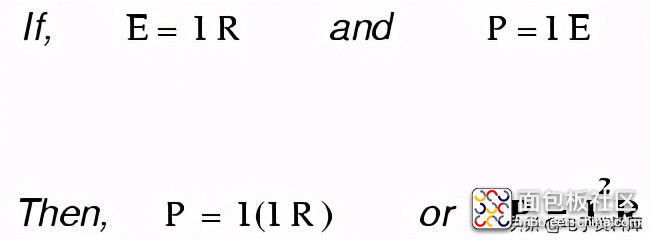
一个历史的注解:是詹姆斯·普雷斯科特·焦耳,而不是乔治·西蒙·欧姆,第一个发现了功耗和通过电阻的电流之间的数学关系。这一发现发表于1841年,遵循了最后一个方程(P=I twoR)的形式,被恰当地称为焦耳定律。然而,这些功率方程通常与有关电压、电流和电阻(E=IR;I=E/R;R=E/I)的欧姆定律方程联系在一起,因此它们常常被认为是欧姆。
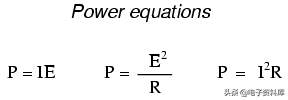
- 回顾:
- 功率测量单位瓦特,以字母“W”表示
- Joule's Law: P = I twoR ; P = IE ; P = E two/R
电阻器
由于任何电路中的电压、电流和电阻之间的关系是如此的有规律,我们可以通过简单地控制另外两个变量来可靠地控制电路中的任何变量。也许在任何电路中最容易控制的变量就是电阻。这可以通过改变其导电部件的材料、尺寸和形状来实现(还记得灯的金属细丝是如何产生比粗电线更大的电阻的吗?)。
调用的特殊组件电阻器是为了产生精确数量的电阻,以便插入电路。它们通常由金属丝或碳纤维构成,并在广泛的环境条件下保持稳定的电阻值。与灯不同,它们不发光,但在工作电路中,当电能被它们消散时,它们确实会产生热量。一般来说,电阻器的作用不是产生可用的热量,而是提供精确的电阻量。
电阻器最常见的示意图符号是锯齿线:

以欧姆为单位的电阻值通常显示为一个相邻的数字,如果一个电路中存在多个电阻器,它们将被标记为一个唯一的标识符编号,如R one,右 two,右 three,等等。如您所见,电阻器符号可以水平或垂直显示:
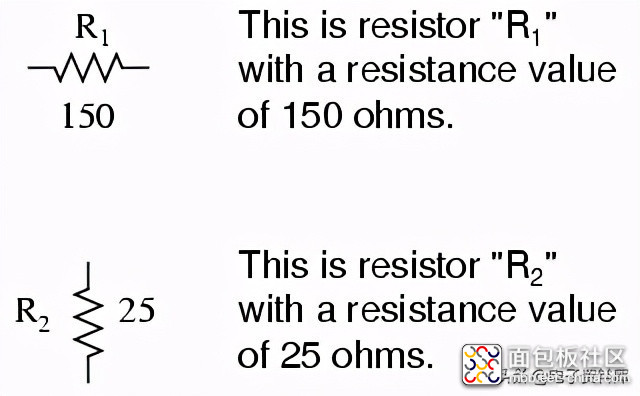
真正的电阻看起来一点也不像锯齿形符号。相反,它们看起来像是有两根电线伸出连接电路的小管子或圆柱体。以下是不同类型和尺寸电阻器的抽样:

为了更符合其物理外观,电阻器的另一个示意图符号看起来像一个长方形的小盒子:

电阻器也可以显示为具有可变电阻而不是固定电阻。这可能是为了描述为提供可调电阻而设计的实际物理设备,也可能是为了显示某些恰好具有不稳定电阻的部件:

事实上,每当你看到一个用对角箭头绘制的元件符号时,该元件就有一个变量,而不是一个固定值。这个符号“修饰符”(对角线箭头)是标准的电子符号惯例。
可变电阻器必须有一些物理调整手段,可以是旋转轴或杠杆,可以移动来改变电阻的大小。这是一张照片展示了一些叫做电位器,可用作可变电阻器:

因为电阻器会随着电流克服其电阻的“摩擦”而耗散热能,因此电阻器也会根据其在不过热和持续损坏的情况下能散发多少热能来进行评级。当然,这种额定功率是以“瓦特”的物理单位来规定的。在小型电子设备(如便携式收音机)中,大多数电阻的额定值为1/4(0.25)瓦或以下。任何电阻器的额定功率与它的物理尺寸大致成正比。在第一张电阻照片中,请注意功率额定值与尺寸的关系:电阻器越大,其功耗额定值越高。还要注意电阻(欧姆)与尺寸无关!
尽管现在让一个器件除了抵抗电流什么都不做似乎毫无意义,但电阻器在电路中是非常有用的器件。因为它们很简单,而且在整个电力和电子领域都被广泛使用,所以我们将花费大量的时间来分析由电阻和电池组成的电路。
要想了解电阻的实用性,请查看下面的照片。这是一张印刷电路板,或印刷电路板:由绝缘酚醛纤维板和导电铜带夹层制成的一种组件,组件可通过称为“焊接”的低温焊接工艺插入和固定。该电路板上的各种组件由印刷标签标识。电阻器用字母“R”开头的任何标签表示。

这个特殊的电路板是一种称为“调制解调器”的计算机附件,它允许通过电话线传输数字信息。在这个调制解调器的板上可以看到至少一打电阻(所有电阻的额定功率为1/4瓦)。每一个黑色矩形(称为“集成电路”或“芯片”)也包含其内部功能所需的电阻阵列。
另一个电路板的例子显示了封装在更小单元中的电阻,称为“表面贴装器件”。这个特殊的电路板是个人电脑硬盘驱动器的底面,焊接在上面的电阻器再次用字母“R”开头的标签标识:

在这个电路板上有100多个表面贴装电阻器,这个数字当然不包括黑色“芯片”内部电阻的数量。这两张照片应该能让任何人相信电阻——那些“仅仅”反对电子流动的器件——是电子领域中非常重要的元件!
在原理图中,电阻符号有时用来说明电路中任何一般类型的器件,它们都可以利用电能来做一些有用的事情。任何非特定的电气设备通常称为负载,所以如果你看到一个示意图,显示了一个标记为“负载”的电阻符号,特别是在一个教程电路图中,解释了一些与实际使用电力无关的概念,那么这个符号可能只是一种比电阻更实际的东西的速记表示。
为了总结我们在本课中学到的知识,让我们分析以下电路,从给出的信息中确定我们能做的一切:
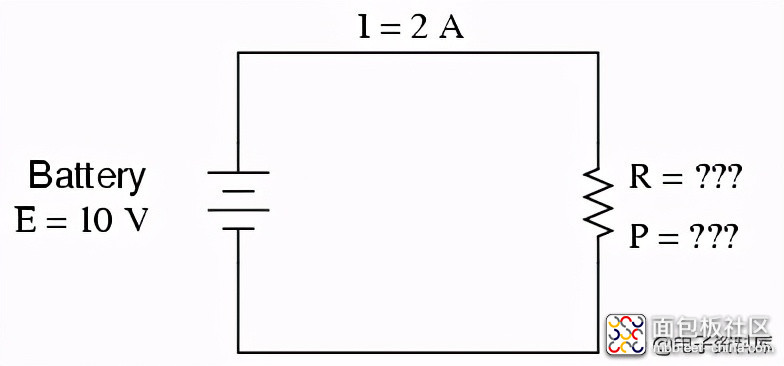
我们在这里所给的只是电池电压(10伏)和电路电流(2安培)。我们不知道电阻的电阻(单位:欧姆)或消耗的功率(瓦特)。通过对欧姆定律方程组的研究,我们发现两个方程组可以从已知的电压和电流量中得出答案:
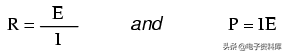
将已知的电压(E)和电流(I)插入这两个方程中,我们可以确定电路电阻(R)和功耗(P):
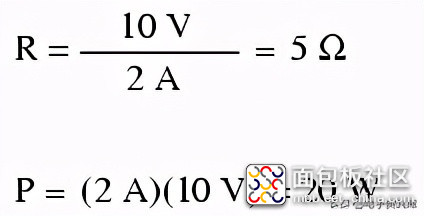
对于10伏和2安培的电路条件,电阻器的电阻必须为5Ω。如果我们要设计一个在这些值下工作的电路,我们必须指定一个最小额定功率为20瓦的电阻器,否则它会过热并发生故障。
- 回顾:
- 调用的设备电阻器在电路中提供精确的电阻。电阻器根据其电阻(欧姆)和散热能力(瓦特)进行评级。
- 电阻器的电阻额定值不能根据电阻器的物理尺寸来确定,尽管近似的功率额定值可以。电阻越大,在不受损害的情况下,可以安全耗散的功率就越大。
- 任何利用电力执行某些有用任务的设备通常被称为负载. 有时在示意图中使用电阻符号来表示非特定负载,而不是实际电阻器。
非线性传导
“进步是通过回答问题来实现的。发现是通过质疑答案来实现的。”
Bernhard Haisch, Astrophysicist
欧姆定律是一个简单而有力的数学工具,可以帮助我们分析电路,但它也有局限性,我们必须了解这些局限性,以便正确地将其应用到实际电路中。对大多数导体来说,电阻是一种相当稳定的特性,很大程度上不受电压或电流的影响。因此,我们可以把许多电路元件的电阻看作一个常数,电压和电流直接相关。
例如,我们前面的电路例子中的3Ω灯,我们通过将电压除以电阻(I=E/R)来计算通过电路的电流。使用18伏电池,我们的电路电流为6安培。将电池电压加倍至36伏,产生12安培的电流加倍。当然,所有这些都是有意义的,只要灯继续为通过它的电子流提供完全相同的摩擦力(电阻):3Ω。
然而,现实并不总是如此简单。在后面一章中探讨的现象之一是导体电阻改变随温度变化。在白炽灯中(利用电流加热细丝使其发出白热的原理),当白炽灯从室温加热到工作温度时,其电阻会急剧增加。如果我们要在一个实际的灯电路中增加电源电压,电流的增加会导致灯丝温度升高,而这又会增加其电阻,从而防止电流进一步增加而电池电压不会进一步增加。因此,电压和电流不遵循简单的公式“I=E/R”(假设R等于3Ω),因为白炽灯的灯丝电阻在不同的电流下不保持稳定。
电阻随温度变化而变化的现象几乎是所有金属的共同现象,大多数金属丝都是这样做的。对于大多数应用,电阻的这些变化很小,可以忽略不计。在灯丝的应用中,金属丝的变化比较大。
这只是电路中“非线性”的一个例子。这绝不是唯一的例子。数学中的“线性”函数是指在图形上绘制时跟踪直线的函数。灯丝电阻恒定为3Ω的灯电路的简化版本生成如下图:
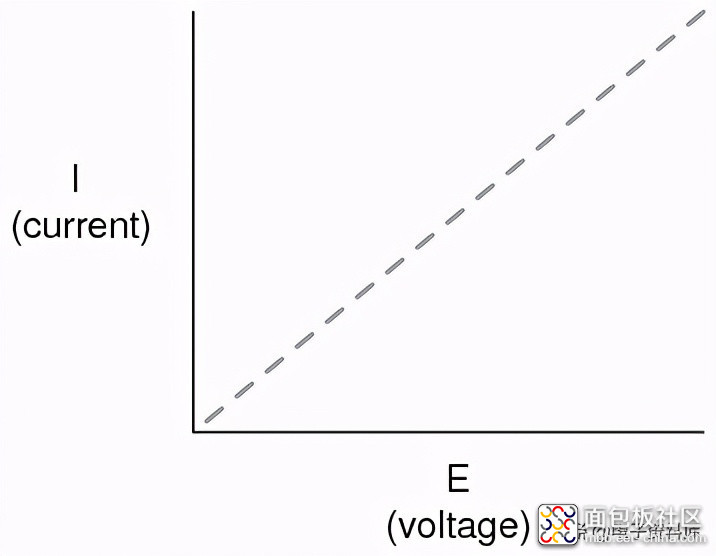
电流过电压的直线图表明,电阻在很大的电路电压和电流范围内是一个稳定不变的值。在“理想”的情况下,情况就是这样。制造电阻器的目的是提供一个确定的、稳定的电阻值,其行为与上面所示的数值图非常相似。数学家会把它们的行为称为“线性的”
然而,对灯电路进行更实际的分析时,在几个不同的电池电压值下,会生成一个这种形状的图:
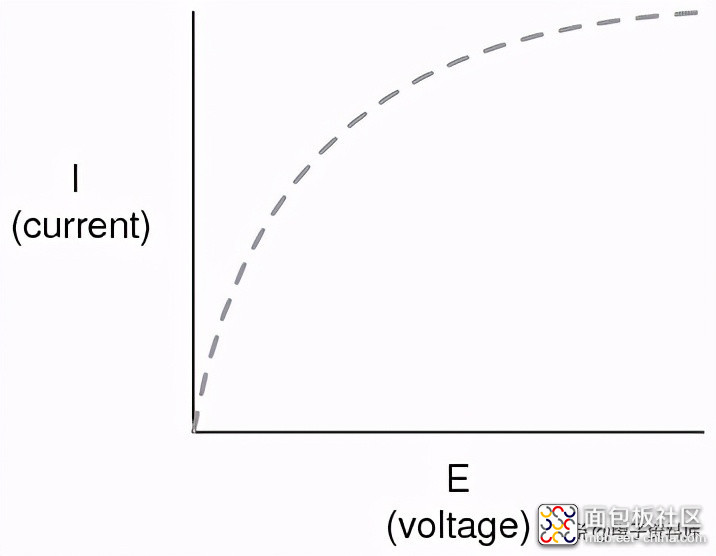
情节不再是一条直线。当电压从零上升到较低水平时,左侧电压急剧上升。当它向右边发展时,我们看到线路变平了,电路需要越来越大的电压增加来达到相等的电流增加。
如果我们试着用欧姆定律,用上面画出的电压和电流值来求这个灯电路的电阻,我们会得到几个不同的值。我们可以说这里的阻力是非线性随着电流和电压的增加而增加。非线性是由灯丝的金属丝受高温影响而引起的。
另一个非线性电流传导的例子是通过空气等气体。在标准温度下,空气绝缘体是有效的。然而,如果被气隙隔开的两个导体之间的电压增加到足够大的程度,间隙之间的空气分子就会“电离”,它们的电子会被导线之间的高压所剥离。一旦电离,空气(和其他气体)就成为良好的导电体,允许电子在电离之前不可能存在的地方流动。如果我们像对灯电路那样在图表上绘制电流过电压图,电离效应会明显地被视为非线性:
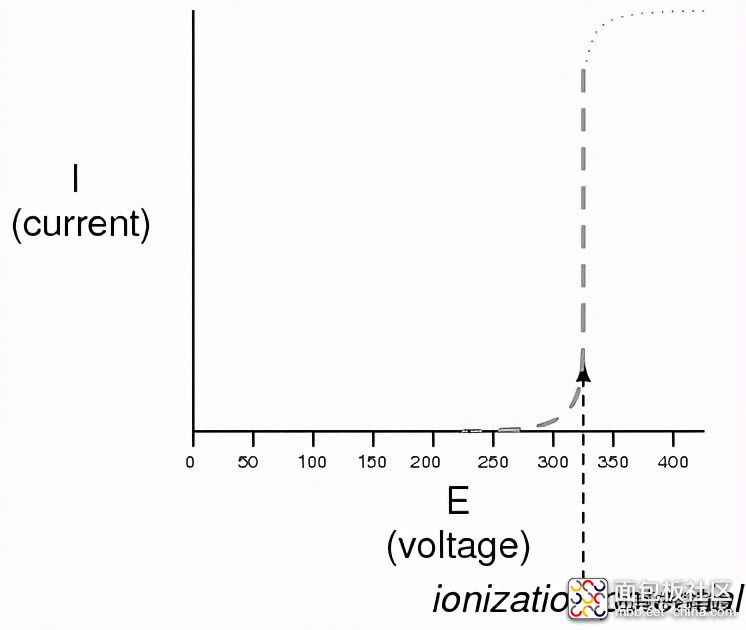
图中所示为小气隙(小于1英寸)的近似值。较大的气隙会产生更高的电离势,但I/E曲线的形状将非常相似:在达到电离电位之前几乎没有电流,然后是实质性的传导。
顺便说一句,这就是闪电以瞬间的浪涌而不是连续的电子流存在的原因。在地球和云层(或不同的云层之间)之间建立的电压必须增加到一定程度,在空气电离到足以支持大量电子流动之前,它必须克服气隙的电离势。一旦这样,电流将继续通过电离空气传导,直到两点之间的静电荷耗尽。一旦电荷耗尽,电压降到另一个阈值以下,空气就会电离,并返回到电阻极高的正常状态。
许多固体绝缘材料表现出类似的电阻特性:在低于某个临界阈值电压时,对电子流的电阻极高,而在超过该阈值的电压下,电阻会大大降低。一旦固体绝缘材料被高压破坏崩溃正如它所说,它通常不会回到以前的绝缘状态,不像大多数气体。它可以在低电压下再次绝缘,但是它的击穿阈值电压将降低到某个较低的水平,这可能使将来更容易发生击穿。这是高压线路常见的故障模式:击穿造成的绝缘损坏。可使用1000伏以上的特殊电压表检测出故障。
有专门设计的电路元件可以提供非线性电阻曲线,其中之一就是变阻器. 这些器件通常由氧化锌或碳化硅等化合物制成,在达到一定的“点火”或“击穿”电压(相当于气隙的“电离电位”)之前,它们的端子之间保持着高电阻,此时它们的电阻会急剧下降。与绝缘体的击穿不同,压敏电阻击穿是可重复的:也就是说,它被设计成能够承受反复的故障而不会发生故障。此处显示变阻器的图片:

也有一些特殊的充气管,设计用来做同样的事情,在闪电使空气电离的过程中利用了同样的原理。
其他电气元件的电流/电压曲线甚至比这更奇怪。有些设备实际上会经历减少电流作为外加电压增加. 因为这种现象的电流/电压的斜率是负的(从左到右,它是向下的而不是向上的),它被称为负电阻 .
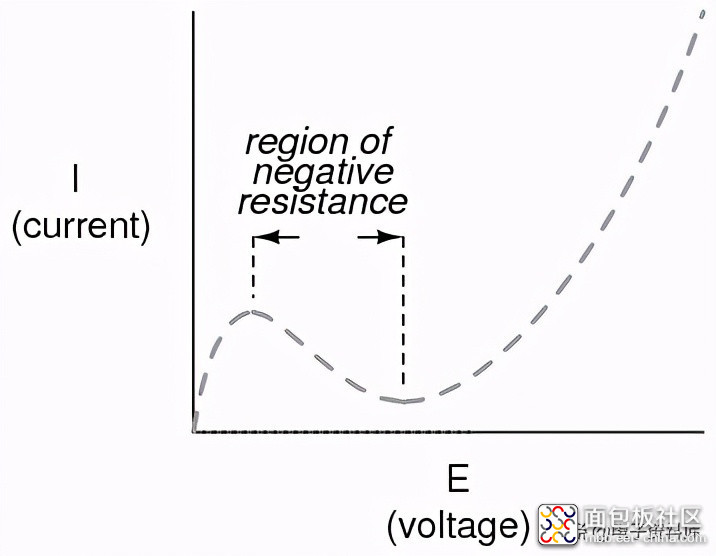
最值得注意的是,高真空电子管tetrodes半导体二极管Esaki或隧道二极管在一定的外加电压范围内表现出负电阻。
欧姆定律对于分析电阻随电压和电流变化的元件的行为不是很有用。有些人甚至建议“欧姆定律”应该从“定律”的地位降级,因为它不具有普遍性。把方程(R=E/I)称为a可能更准确,阻力的定义适用于某一类材料在较窄的条件下。
然而,为了学生的利益,我们将假设示例电路中指定的电阻是除非另有规定,否则在各种条件下稳定。我只想让你们了解一下现实世界的一点复杂性,以免给你们一个错误的印象,即整个电现象可以用几个简单的方程式来概括。
- 回顾:
- 大多数导电材料的电阻在各种条件下都是稳定的,但并非所有材料都是如此。
- 任何可以在图上绘制为直线的函数称为线性的函数。对于电阻稳定的电路,电流过电压曲线呈线性(I=E/R)。
- 在电阻随电压或电流变化而变化的电路中,电流过电压曲线图为非线性(不是直线)
- A变阻器是一种随外加电压的变化而改变电阻的元件。由于电压很低,它的电阻很高。然后,在一定的“击穿”或“点火”电压下,它的电阻急剧下降。
- 负电阻当外加电压增加时,通过元件的电流实际上会减少。特别是电子管和半导体二极管四极管管子和Esaki,或隧道二极管)在一定的电压范围内表现出负电阻。
电路布线
到目前为止,我们一直在分析单电池、单电阻电路,而不考虑组件之间的连接线,只要形成完整的电路。导线长度或电路“形状”对我们的计算有影响吗?让我们看看几个电路配置,然后找出:
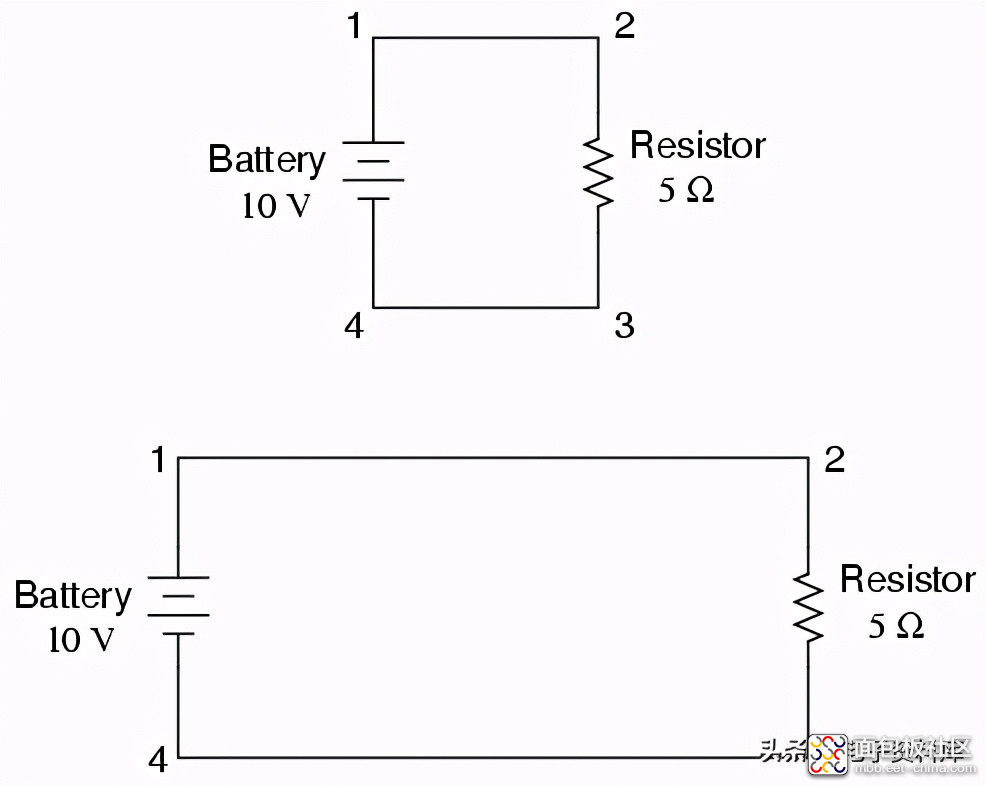
当我们画电路中连接点的导线时,我们通常假定这些导线的电阻可以忽略不计。因此,它们对电路的整体电阻没有明显的影响,因此我们要对付的唯一电阻就是元件中的电阻。在上述电路中,唯一的电阻来自5Ω的电阻,所以我们在计算时只考虑这一点。在现实生活中,金属丝做有阻力(电源也是如此!),但这些电阻通常比其他电路元件中的电阻小得多,因此可以安全地忽略它们。在正常情况下,如果导线的电流(即使是很小的电压水平)也会产生非常大的电流降。
如果连接线电阻很小或没有,我们可以将电路中的连接点视为电气通用. 也就是说,上述电路中的点1和点2可以物理连接在一起,也可以相距很远,对于与这些点相关的任何电压或电阻测量来说,这都无关紧要。第3点和第4点也是如此。就欧姆定律计算和电压测量而言,就好像电阻的两端直接连接在电池的端子上一样。知道这一点很有用,因为这意味着您可以重新绘制电路图或重新布线,根据需要缩短或延长导线,而不会明显影响电路的功能。重要的是这些组件以相同的顺序彼此连接。
这也意味着两组“电气公共”点之间的电压测量值将是相同的。也就是说,点1和点6(直接穿过蓄电池)之间的电压将与点3和点4(直接穿过电阻器)之间的电压相同。仔细观察以下电路,并尝试确定哪些点是彼此共有的:
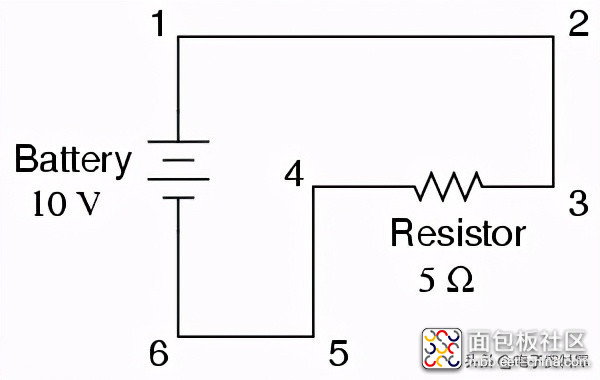
在这里,我们只有两个组件,除了电线:电池和电阻器。虽然连接线在形成一个完整的电路时走的是一条曲折的路径,但在电子的路径上有几个共同点。点1、点2和点3彼此都是公共的,因为它们通过导线直接连接在一起。第4点、第5点和第6点也是如此。
点1和点6之间的电压是10伏,直接来自蓄电池。然而,由于点5和点4是6的公共点,而点2和点3是1的公共点,所以这些其他点对之间也存在相同的10伏电压:
Between points 1 and 4 = 10 volts Between points 2 and 4 = 10 volts Between points 3 and 4 = 10 volts (directly across the resistor) Between points 1 and 5 = 10 volts Between points 2 and 5 = 10 volts Between points 3 and 5 = 10 volts Between points 1 and 6 = 10 volts (directly across the battery) Between points 2 and 6 = 10 volts Between points 3 and 6 = 10 volts
复制代码由于电气公共点是通过(零电阻)导线连接在一起的,因此无论通过该连接线从一个点传导到另一个点的电流量如何,它们之间都没有明显的电压降。因此,如果我们要读取公共点之间的电压,我们应该(实际上)显示零:
Between points 1 and 2 = 0 volts Points 1, 2, and 3 are Between points 2 and 3 = 0 volts electrically common Between points 1 and 3 = 0 volts Between points 4 and 5 = 0 volts Points 4, 5, and 6 are Between points 5 and 6 = 0 volts electrically common Between points 4 and 6 = 0 volts
复制代码这在数学上也是有道理的。如果使用10伏蓄电池和5Ω电阻器,电路电流将为2安培。当导线电阻为零时,可通过欧姆定律确定任何连续导线的电压降:
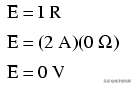
很明显,在假定导线电阻为零的电路中,通过任何不间断导线长度计算的电压降始终为零,无论电流大小,因为零乘以任何值等于零。
由于电路中的公共点将显示相同的相对电压和电阻测量值,连接公共点的导线通常标有相同的名称。这并不是说终端连接点的标签是相同的,只是连接线。以这条线路为例:
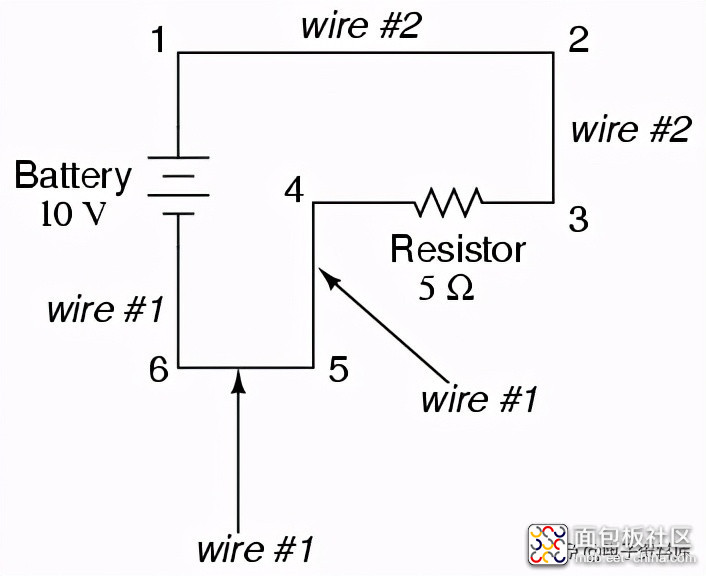
点1、2和3彼此都是公用的,因此连接点1到2的导线标记为与连接点2到3(导线2)相同的标记(导线2)。在实际电路中,从点1延伸到点2的导线甚至可能与连接点2到点3的导线颜色或尺寸不同,但它们应带有完全相同的标签。连接点6、5和4的导线也是如此。
了解电气公共点之间的电压降为零是一个有价值的故障排除原则。如果我测量一个电路中被认为是彼此共用的点之间的电压,我的读数应该是零。然而,如果我读到这两点之间的电压,那么我肯定地知道它们不能直接连接在一起。如果这些点是想象上的在电上是普通的,但它们不是这样的,那么我知道在这些点之间有一个“开放性故障”。
最后一点要注意的是:对于大多数实际用途,可以假设导线导线端到端的电阻为零。然而,实际上,在导线的长度上总会遇到一些小电阻,除非是超导导线。知道了这一点,我们需要记住,这里所学的关于电公共点的原理在很大程度上都是有效的,但对绝对的学位。也就是说,保证电气公共点之间有零电压的规则被更准确地表述为:电气公共点将很少他们之间的电压下降了。在任何一根连接线中发现的微小的,几乎不可避免的电阻痕迹,当电流通过时,必然会在其长度上产生一个小电压。只要你明白这些规则是基于理想的条件,你不会感到困惑,当你遇到一些条件似乎是一个例外的规则。
- 回顾:
- 除非另有说明,否则电路中的连接线均假定为零电阻。
- 电路中的导线可以被缩短或加长而不影响电路的功能——重要的是元件以相同的顺序彼此连接。
- 在电路中通过零电阻(导线)直接连接在一起的点被认为是电气通用 .
- 电气公共点之间的电阻为零,它们之间的电压降为零,而不考虑电流的大小(理想情况下)。
- 两组电气公共点之间参考的电压或电阻读数应相同。
- 这些规则适用于理想的假设连接线具有绝对零电阻的条件。在现实生活中,这种情况可能不会发生,但导线电阻应足够低,以便这里所述的一般原则仍然适用。
电压降极性
我们可以通过从负极(-)端子开始,一直到蓄电池的正极()端子(电路中唯一的电压源),来追踪电子在同一电路中流动的方向。从这里我们可以看到,电子是逆时针运动的,从6点到5点,4点,3点,2点到1点,再回到6点。
当电流遇到5Ω电阻时,电阻两端的电压就会下降。此电压降的极性在点4处为负(-)相对于点3的正极()。我们可以根据电流的方向(无论电阻的哪一端是电流),用这些正负符号来标记电阻器电压降的极性套房相对于电阻的末端是负的退出 :
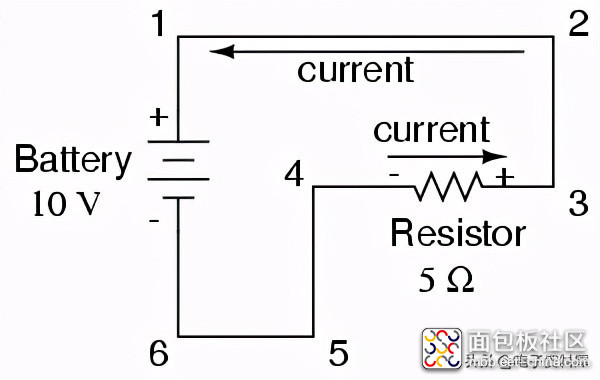
通过标记电路中每对点的电压极性,我们可以使电压表更加完整:
Between points 1 (+) and 4 (-) = 10 volts Between points 2 (+) and 4 (-) = 10 volts Between points 3 (+) and 4 (-) = 10 volts Between points 1 (+) and 5 (-) = 10 volts Between points 2 (+) and 5 (-) = 10 volts Between points 3 (+) and 5 (-) = 10 volts Between points 1 (+) and 6 (-) = 10 volts Between points 2 (+) and 6 (-) = 10 volts Between points 3 (+) and 6 (-) = 10 volts
复制代码虽然在这个电路中记录电压降的极性似乎有点愚蠢,但掌握它是一个重要的概念。在分析涉及多个电阻和/或电池的更复杂电路时,这一点至关重要。
应该理解的是,极性与欧姆定律无关:在欧姆定律方程中永远不会有负电压、电流或电阻!还有其他一些电的数学原理,通过使用符号(或-)来考虑极性,但没有欧姆定律。
- 回顾:
- 通过任何电阻元件的电压降的极性取决于通过它的电子流的方向:消极的进入,和积极的正在退出
电路的计算机模拟
如果使用得当,计算机可以成为强有力的工具,特别是在科学和工程领域。计算机模拟电路的软件是存在的,这些程序可以帮助电路设计者在实际构建电路之前测试想法,从而节省大量的时间和金钱。
这些同样的程序对于电子学的初学者来说是一个极好的辅助工具,可以让他们快速而轻松地探索思想,而不需要组装真正的电路。当然,没有什么可以代替实际构建和测试真实电路的方法,但是计算机模拟确实有助于学习过程,让学生体验变化,并看到它们对电路的影响。在这本书中,我将结合从电路模拟经常计算机打印输出,以说明重要的概念。通过观察计算机模拟的结果,学生可以直观地掌握电路的行为,而不必受到抽象数学分析的威胁。
为了在计算机上模拟电路,我使用了一个名为SPICE的特殊程序,它通过文本列表向计算机描述电路。本质上,这个列表本身就是一种计算机程序,必须遵守SPICE语言的语法规则。然后用计算机处理或“运行”SPICE程序,该程序解释描述电路的文本列表,并以文本形式输出详细的数学分析结果。本书系列的第5卷(“参考”)中描述了使用SPICE的许多细节,以供需要更多信息的人使用。在这里,我将介绍一些基本概念,然后将SPICE应用到我们所读到的这些简单电路的分析中。
首先,我们需要在我们的计算机上安装SPICE。作为一个免费的程序,它通常可以在因特网上下载,并且格式适合许多不同的操作系统。在本书中,我使用了SPICE的早期版本之一:版本2G6,因为它的使用简单。
接下来,我们需要一个SPICE分析电路。让我们来试试本章前面介绍的电路之一。这是它的示意图:
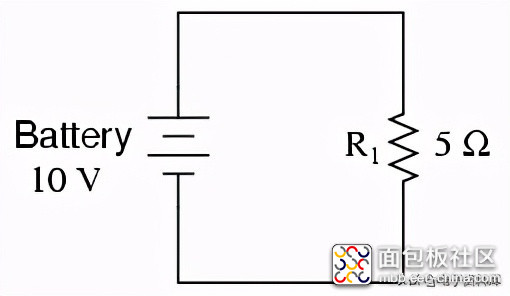
这个简单的电路由一个电池和一个直接连接在一起的电阻器组成。我们知道蓄电池的电压(10伏)和电阻器的电阻(5Ω),但对电路一无所知。如果我们用SPICE来描述这个电路,它应该能够(至少)用欧姆定律(I=E/R)告诉我们电路中有多少电流。
SPICE无法直接理解示意图或任何其他形式的图形描述。SPICE是一个基于文本的计算机程序,它要求根据电路的组成部分和连接点来描述电路。电路中的每个唯一连接点都用一个“节点”编号来描述。在要模拟的电路中彼此电共有的点通过共享相同的数目来指定为这样的点。按照上一节中给出的定义,将这些数字视为“线”号而不是“节点”号可能会有帮助。这就是计算机如何知道什么与什么相连:通过共享公共线或节点、数字。在我们的示例电路中,我们只有两个“节点”,顶部导线和底部导线。SPICE要求在电路中的某个地方有一个节点0,所以我们将给电线0和1贴上标签:
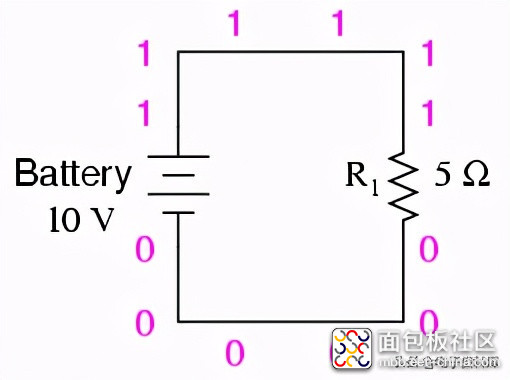
在上面的插图中,我在每条导线周围显示了多个“1”和“0”标签,以强调共享公共节点号的公共点的概念,但这仍然是一个图形图像,而不是文本描述。SPICE需要以文本形式提供组件值和节点号,然后才能进行任何分析。
在计算机中创建文本文件需要使用一个名为文本编辑器. 与文字处理器类似,文本编辑器允许您键入文本并以存储在计算机硬盘上的文件的形式记录键入的内容。文本编辑器缺乏文字处理程序的格式化能力(没有italic ,大胆的,或下划线的字符),这是一件好事,因为SPICE这样的程序不知道如何处理这些额外的信息。如果我们想创建一个纯文本文件,除了我们选择的键盘字符之外,没有任何记录,文本编辑器就是一个可以使用的工具。
如果使用的是微软操作系统,比如DOS或Windows,那么系统中就可以使用一些文本编辑器。在DOS里,有老的编辑文本编辑程序,可通过键入编辑在命令提示下。在Windows(3.x/95/98/NT/Me/2k/XP)中便条簿文本编辑器是你的首选。还有许多其他的文本编辑程序,有些甚至是免费的。我碰巧使用了一个名为维姆,并在windows95和Linux操作系统下运行它。使用哪种编辑器无关紧要,所以不要担心本节中的屏幕截图与您的截图不一样;这里的重要信息是你输入什么,不是哪个编辑你碰巧用了
为了向SPICE描述这个简单的双元件电路,我将首先调用我的文本编辑器程序并为电路输入“title”行:
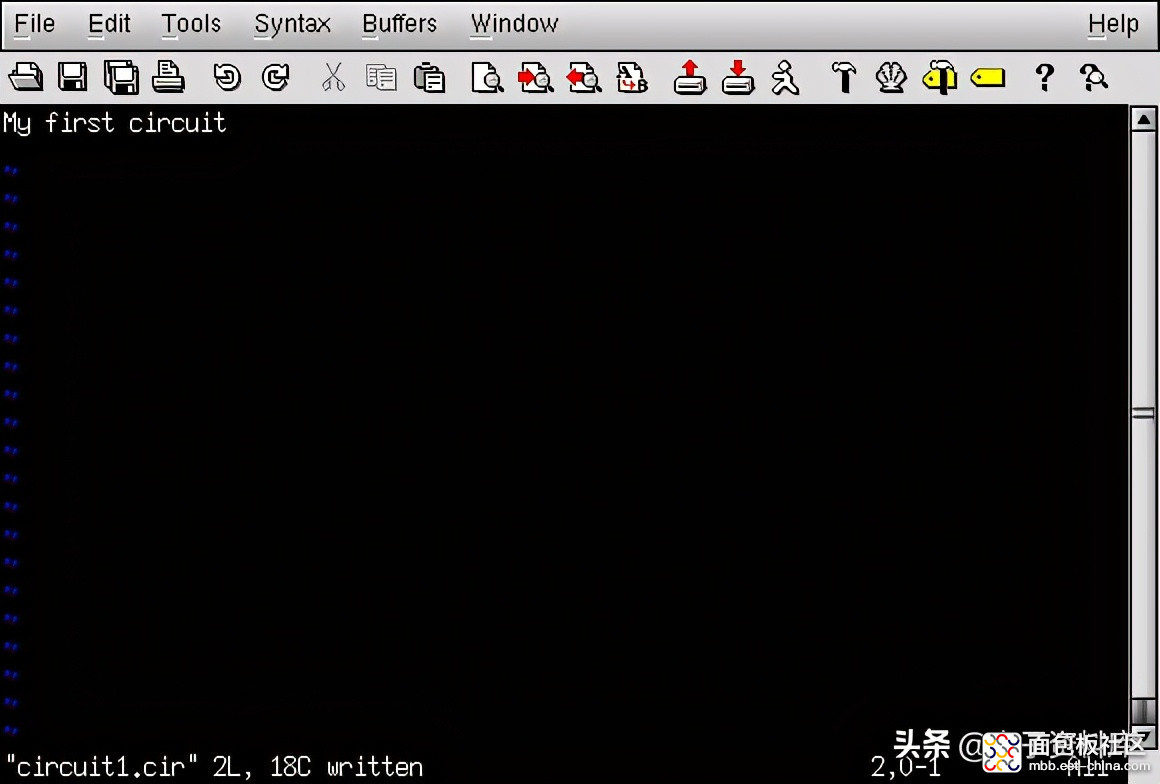
我们可以通过键入以字母开头的一行文字来向计算机描述电池五“(对于“电压源”),识别每个电池端子连接的电线(节点号)和电池电压,如下所示:
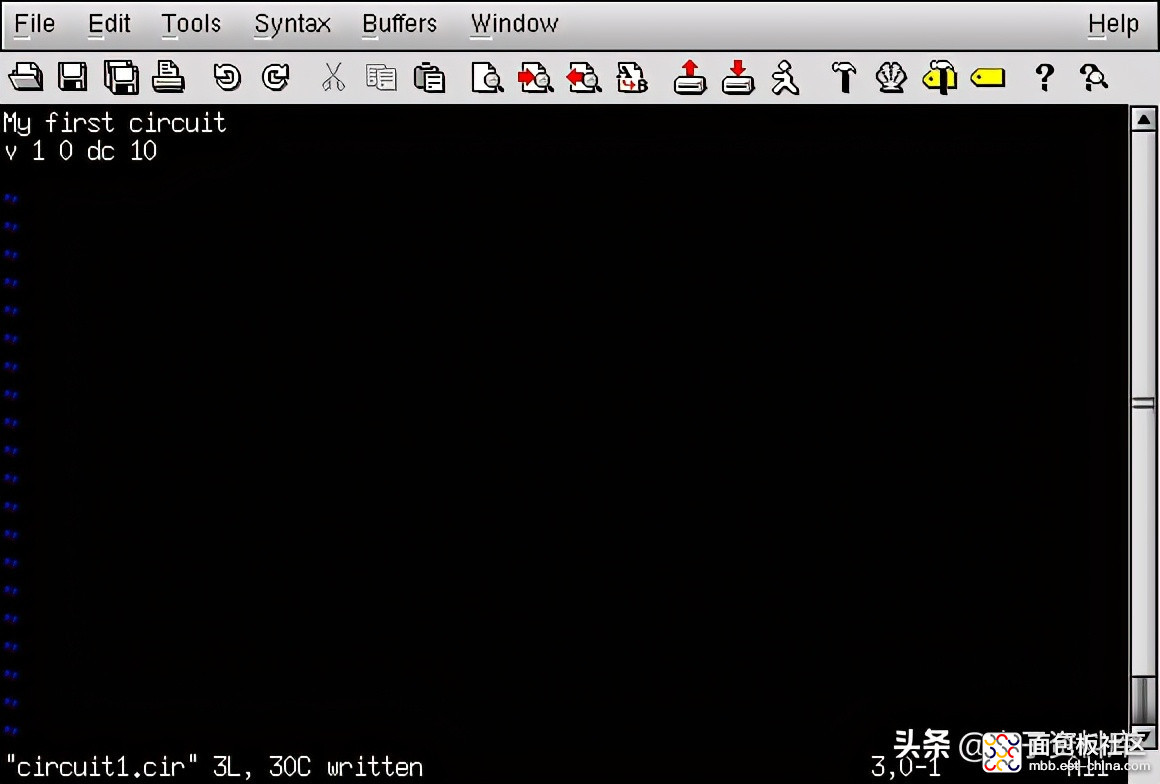
这行文字告诉SPICE,我们在节点1和节点0之间连接了一个电压源,直流电(DC),10伏。这就是计算机需要知道的关于电池的所有信息。现在我们来看看电阻:SPICE要求用字母“r”来描述电阻,两个节点(连接点)的数量,以及电阻的欧姆数。由于这是计算机模拟,因此不需要指定电阻器的额定功率。这是“虚拟”组件的一个优点:它们不会被过高的电压或电流损坏!
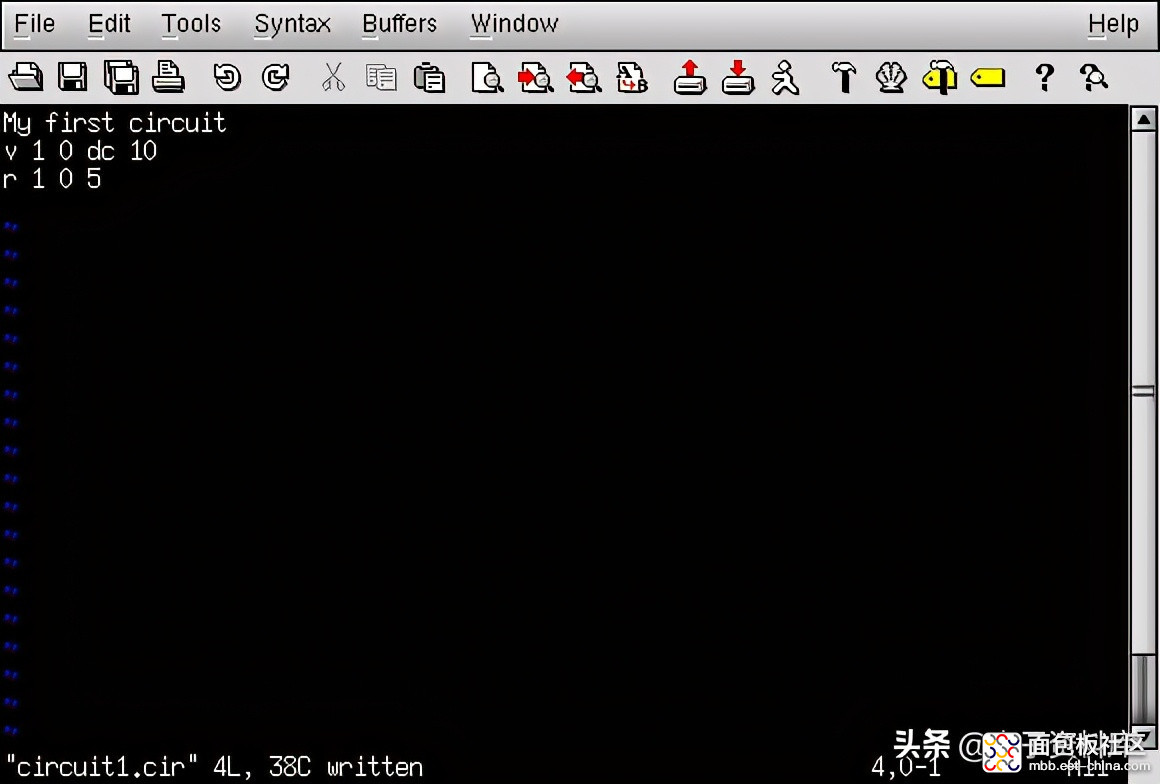
现在,SPICE将知道在节点1和节点0之间有一个电阻值为5Ω。这一行非常简短的文字告诉计算机我们有一个电阻(“r)与电池(1和0)同两个节点之间连接,电阻值为5Ω。
如果我们添加一个.结束语句以这个SPICE命令的集合来表示电路的结束描述,我们将SPICE所需要的所有信息,收集在一个文件中并准备好进行处理。从技术上讲,这是一个由计算机线路组成的文件网络列表,或甲板 :
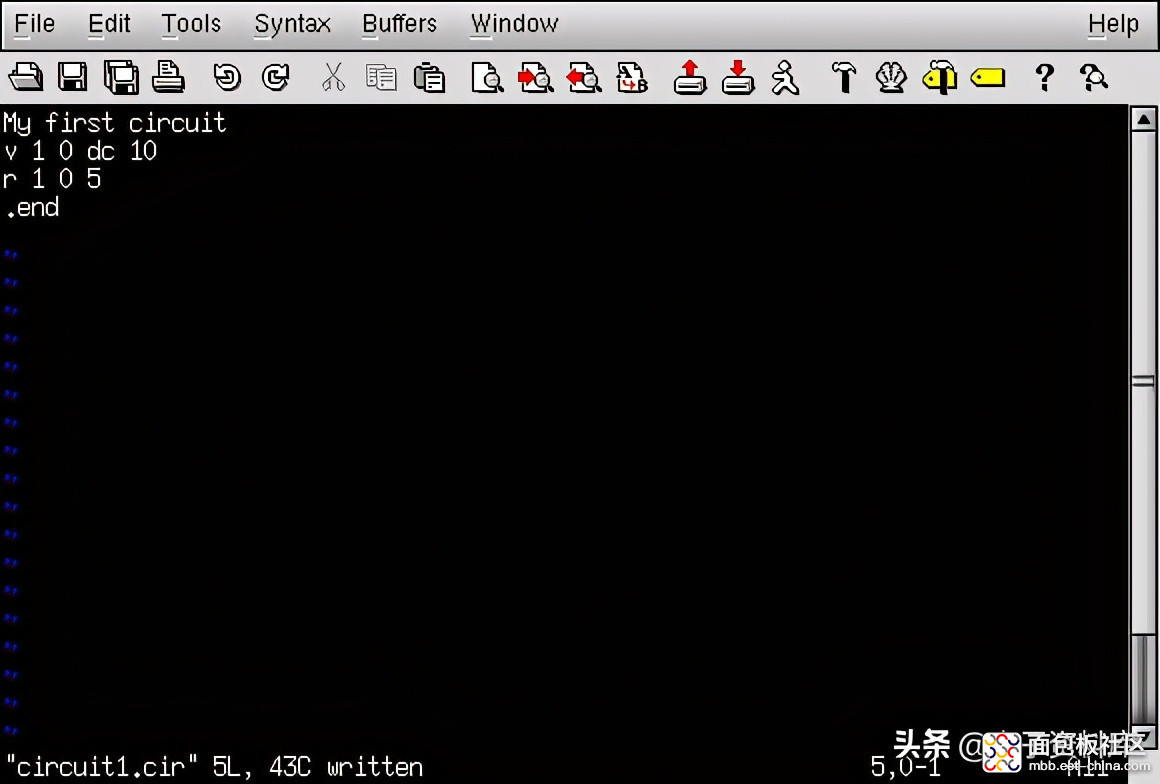
一旦我们完成了所有必要的SPICE命令的输入,我们需要将它们“保存”到计算机硬盘上的一个文件中,这样SPICE在调用时就有一些可以参考的东西。因为这是我的第一个SPICE网络列表,我会把它保存在文件名下“电路1.cir“(实际名称是任意的)。您可以选择将第一个SPICE netlist命名为完全不同的名称,只要您不违反操作系统的任何文件名规则,例如使用不超过83个字符(名称中有8个字符,扩展名中有3个字符:壹仟贰佰叁拾肆万伍仟陆佰柒拾捌元壹角贰分叁分)在DOS中
调用SPICE(告诉它处理电路1.cirnetlist文件),我们必须退出文本编辑器并访问命令提示符(微软用户的“DOS提示符”),在那里我们可以输入文本命令,让计算机的操作系统遵守。对于习惯于“点击式”图形环境的计算机用户来说,这种调用程序的“原始”方式可能看起来过时了,但它是一种非常强大和灵活的方式。记住,你在这里使用SPICE是一种简单的计算机编程形式,你越习惯于给计算机文本形式的命令,而不是简单地用鼠标点击图标图像,你对计算机的掌握就越强。
在命令提示下,键入此命令,然后按[Enter]键(本例使用文件名电路1.cir;如果您为网络列表文件选择了其他文件名,请替换它):
spice < circuit1.cir
复制代码在我按下[Enter]键之前,我的计算机(运行Linux操作系统)上的显示如下:
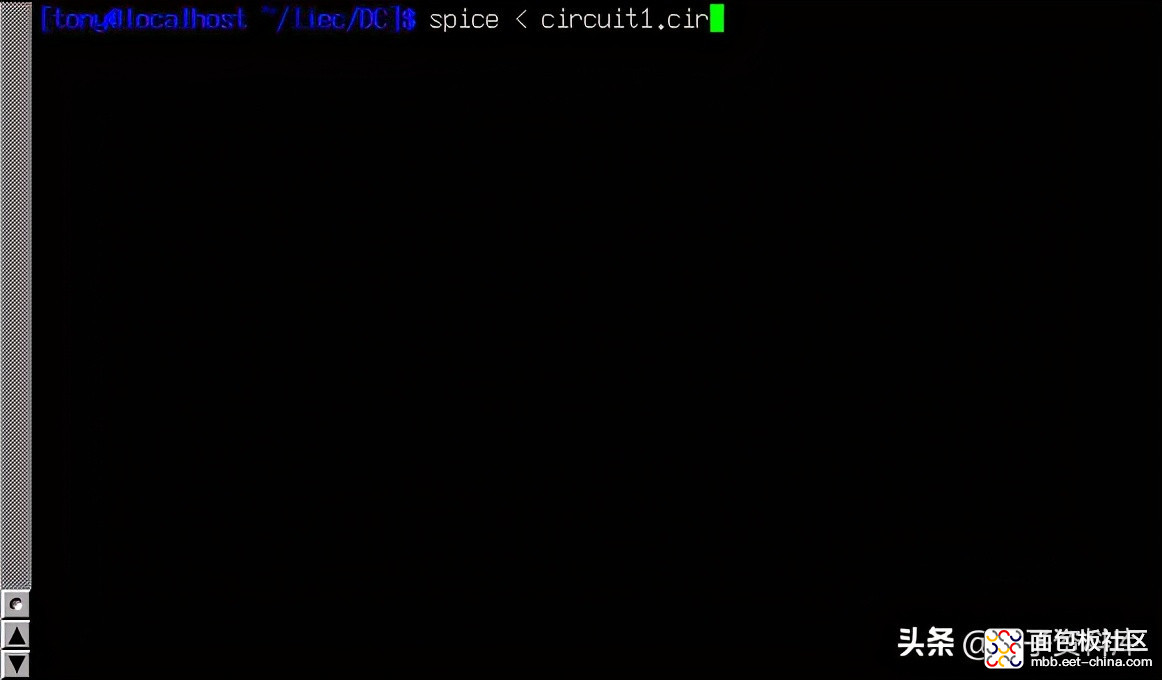
一旦按[Enter]键发出此命令,SPICE输出的文本将在计算机屏幕上滚动。这是一个屏幕截图,显示了SPICE在我的计算机上的输出(我把“终端”窗口加长了,以显示全文)。对于普通尺寸的终端,文本很容易超过一页的长度):
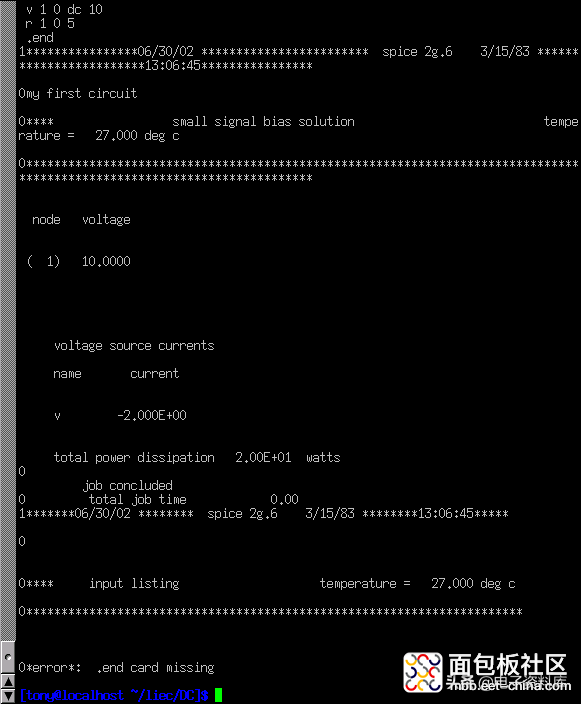
SPICE以重复netlist开始,完成标题行和.结束声明。在模拟进行到一半的时候,它显示了所有节点相对于节点0的电压。在这个例子中,我们只有一个节点而不是节点0,所以它显示那里的电压:10.0000伏。然后显示通过每个电压源的电流。因为整个电路中只有一个电压源,它只显示通过那个电压源的电流。在这种情况下,源电流是2安培。由于SPICE分析电流的方式有点古怪,2安培的值输出为负(-)2安培。
计算机分析报告中的最后一行文字是“总功耗”,在本例中是“2.00e01”瓦特:2.00x10 one或20瓦。SPICE输出的大多数数字是科学记数法,而不是普通(定点)记数法。虽然一开始这似乎更令人困惑,但当涉及到非常大或非常小的数字时,它实际上就不那么令人困惑了。科学记数法的细节将在本书的下一章中讨论。
使用基于文本的“原始”程序(如SPICE)的好处之一是,与其他文件格式相比,处理的文本文件非常小,尤其是在其他电路仿真软件中使用的图形格式。另外,SPICE的输出是纯文本的这一事实意味着您可以将SPICE的输出定向到另一个文本文件中,在那里可以进一步操作它。为此,我们向计算机的操作系统发出一个命令来调用SPICE,这一次将输出重定向到我将调用的文件输出.txt ":
SPICE这次将“静默”运行,而不会像以前那样将文本流输出到计算机屏幕。一个新文件,输出1.txt,将被创建,您可以使用文本编辑器或字处理程序打开并更改。我将使用相同的文本作为插图(维姆)要打开此文件:
现在,我可以自由编辑此文件,删除任何无关的文本(例如显示日期和时间的“横幅”),只留下我认为与电路分析相关的文本:
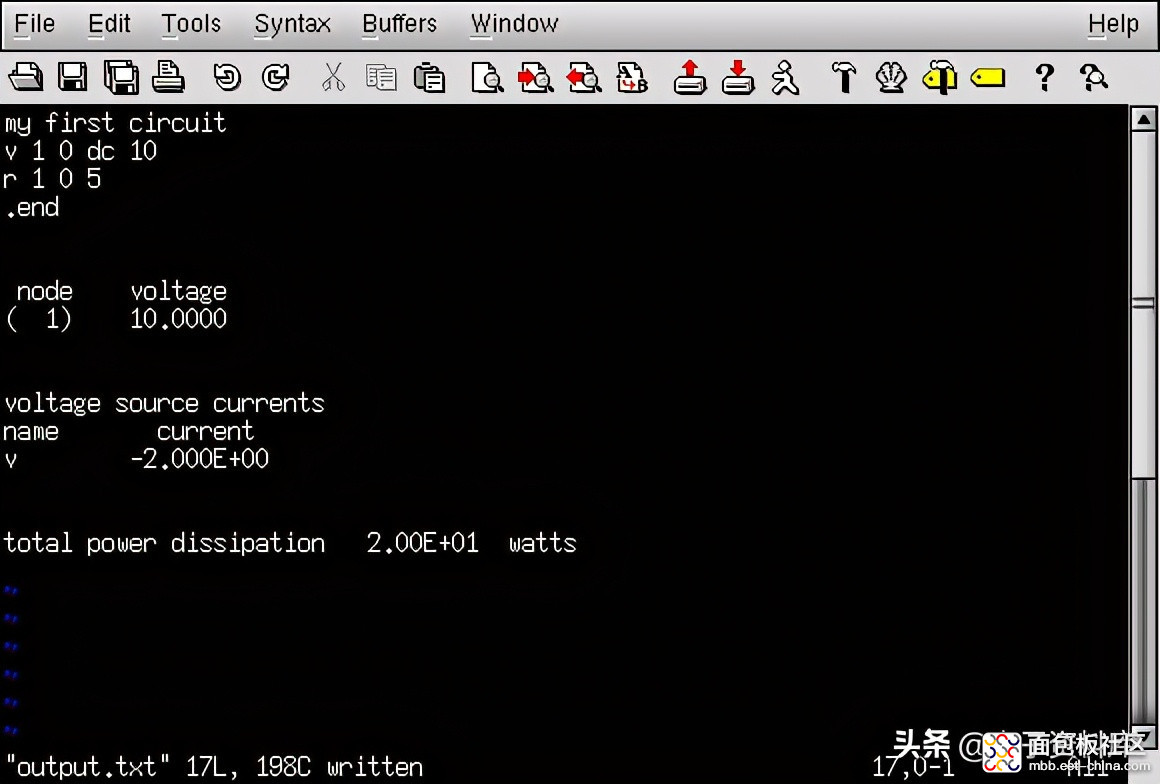
经过适当编辑并重新保存在同一文件名下(输出.txt在本例中),文本可以粘贴到任何类型的文档中,“纯文本”是几乎所有计算机系统的通用文件格式。我甚至可以把它直接包含在这本书的文本中——而不是作为一个“屏幕截图”的图形图像——像这样:
my first circuitv 1 0 dc 10 r 1 0 5 .end
复制代码 node voltage( 1) 10.0000
复制代码voltage source currentsname current v -2.000E+00
复制代码total power dissipation 2.00E+01 watts
复制代码要改变模拟中的组件值,我们需要打开netlist文件(电路1.cir)并在电路的文本描述中进行所需的修改,然后将这些更改保存为相同的文件名,并在命令提示符下重新调用SPICE。编辑和处理文本文件的过程是每个计算机程序员都熟悉的过程。我喜欢教SPICE的原因之一是它能让学习者像计算机程序员一样思考和工作,这很好,因为计算机编程是高级电子工作的一个重要领域。
早些时候,我们研究了改变电路中三个变量中的一个(电压、电流或电阻)的后果,用欧姆定律来数学预测会发生什么。现在让我们用SPICE来做同样的事情。
如果我们把上一个例子电路中的电压从10伏增加到30伏,并且保持电路电阻不变,那么电流也会增加三倍。让我们尝试一下,重新命名我们的网络列表文件,这样就不会重写第一个文件。这样,我们就可以二者都电路模拟的版本储存在我们电脑的硬碟上以备将来使用。以下文本列表是此修改后的网络列表的SPICE输出,格式为纯文本,而不是计算机屏幕的图形图像:
second example circuitv 1 0 dc 30 r 1 0 5 .end
复制代码node voltage( 1) 30.0000
复制代码voltage source currentsname current v -6.000E+00 total power dissipation 1.80E+02 watts
复制代码正如我们预期的那样,电流增加了三倍。电流过去是2安培,现在增加到6安培(-6.000 x 10 zero). 还要注意电路中的总功耗是如何增加的。以前是20瓦,现在是180瓦(1.8×10 two). Recalling that power is related to the square of the voltage (Joule's Law: P=E two/R) 有道理。如果我们把电路电压增加三倍,功率应该增加九倍 two= 9). Nine times 20 is indeed 180, so SPICE's output does indeed correlate with what we know about power in electric circuits.
如果我们想知道这个简单的电路在很大的电池电压范围内如何响应,我们可以调用SPICE中的一些更高级的选项。在这里,我用“.直流电分析选项,以5伏为增量,从0伏到100伏不等,打印出每一步的电路电压和电流。SPICE网络列表中以星号(“ *“)是评论. 也就是说,它们不会告诉计算机做任何与电路分析有关的事情,而只是作为任何人阅读网络列表文本的注释。
third example circuit v 1 0 r 1 0 5 *the ".dc" statement tells spice to sweep the "v" supply *voltage from 0 to 100 volts in 5 volt steps. .dc v 0 100 5 .print dc v(1) i(v) .end
复制代码这个.打印此SPICE netlist中的命令指示SPICE打印与分析中每个步骤对应的数字列:
v i(v) 0.000E+00 0.000E+00 5.000E+00 -1.000E+00 1.000E+01 -2.000E+00 1.500E+01 -3.000E+00 2.000E+01 -4.000E+00 2.500E+01 -5.000E+00 3.000E+01 -6.000E+00 3.500E+01 -7.000E+00 4.000E+01 -8.000E+00 4.500E+01 -9.000E+00 5.000E+01 -1.000E+01 5.500E+01 -1.100E+01 6.000E+01 -1.200E+01 6.500E+01 -1.300E+01 7.000E+01 -1.400E+01 7.500E+01 -1.500E+01 8.000E+01 -1.600E+01 8.500E+01 -1.700E+01 9.000E+01 -1.800E+01 9.500E+01 -1.900E+01 1.000E+02 -2.000E+01
复制代码如果我重新编辑网络列表文件,更改.打印命令转换为.绘图命令,SPICE将输出由文本字符组成的粗略图形:
Legend: + = v#branch ------------------------------------------------------------------------ sweep v#branch-2.00e+01 -1.00e+01 0.00e+00 ---------------------|------------------------|------------------------| 0.000e+00 0.000e+00 . . + 5.000e+00 -1.000e+00 . . + . 1.000e+01 -2.000e+00 . . + . 1.500e+01 -3.000e+00 . . + . 2.000e+01 -4.000e+00 . . + . 2.500e+01 -5.000e+00 . . + . 3.000e+01 -6.000e+00 . . + . 3.500e+01 -7.000e+00 . . + . 4.000e+01 -8.000e+00 . . + . 4.500e+01 -9.000e+00 . . + . 5.000e+01 -1.000e+01 . + . 5.500e+01 -1.100e+01 . + . . 6.000e+01 -1.200e+01 . + . . 6.500e+01 -1.300e+01 . + . . 7.000e+01 -1.400e+01 . + . . 7.500e+01 -1.500e+01 . + . . 8.000e+01 -1.600e+01 . + . . 8.500e+01 -1.700e+01 . + . . 9.000e+01 -1.800e+01 . + . . 9.500e+01 -1.900e+01 . + . . 1.000e+02 -2.000e+01 + . . ---------------------|------------------------|------------------------| sweep v#branch-2.00e+01 -1.00e+01 0.00e+00
复制代码在这两种输出格式中,左边一列数字表示电池电压在每个间隔,从0V增加到100V,每次增加5V。右边栏中的数字表示每个电压对应的电路电流。仔细看看这些数字,你会发现每一对之间的比例关系:欧姆定律(I=E/R)在任何情况下都成立,每个电流值都是各自电压值的1/5,因为电路电阻正好是5 Ω。同样,在香料分析中,电流的负数比其他任何东西都更令人费解。只要注意每个数字的绝对值,除非另有说明。
甚至有一些计算机程序能够解释并将SPICE输出的非图形数据转换成图形图。其中一个程序叫做Nutmeg,其输出如下所示:
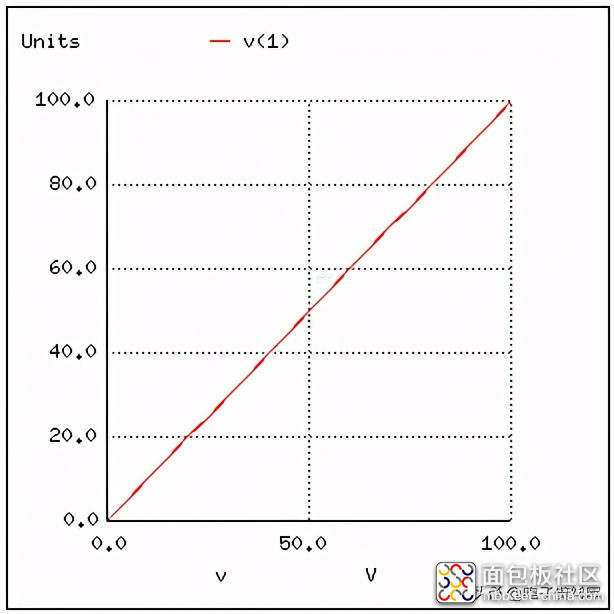
注意如何绘制电阻电压五(1)(节点1和节点0的隐含参考点之间的电压)作为具有正斜率的线(从左下到右上)。
你是否精通使用SPICE与它在本书中的应用无关。重要的是,你要对SPICE生成的报告中数字的含义有一个理解。在接下来的例子中,我将尽我所能注释SPICE的数值结果,以消除任何混淆,并释放这个神奇工具的力量,帮助您理解电路的行为。
来源:电子资料库







 /4
/4 

