

概述
IGBT模块损耗计算对电力电子系统设计至关重要,对损耗的计算主要通过两种途径,一是通过建立电气模型进行系统仿真;另外一种则是根据器件的关键参数,通过数学方法推导损耗公式来计算。通过器件模型仿真的方法需要有器件的电气模型,而往往厂家并不会全部提供器件的电气仿真模型,而且耗时耗力。数学方法计算往往会对器件模型进行简化,因而导致计算结果不准确。本文阐述了一种依据规格书中的特征曲线来准确计算IGBT损耗的方法。该方法通过拟合包括Vce,Vf 等与损耗相关的曲线,获取描述这些曲线的参数方程,同时引入结温变化对特征曲线的影响。然后,结合参数方程,并依据于这些曲线的测量条件来计算准确IGBT的损耗。

基本计算公式
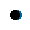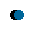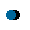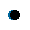
通常的,IGBT 模块损耗包括IGBT 损耗()和DIODE 损耗()两部分。IGBT 损耗包括通态损耗()和开关损耗开通()。开关损耗由开通损耗()和关断损耗()组成。DIODE 损耗包括通态损耗()和反向恢复损耗()。通态损耗的产生是由于电流正向流经IGBT 或者DIODE 会在芯片上产生一定的压降,损耗就是正向电流和器件两端的正向压降的乘积;开关损耗和反向恢复损耗则是跟开关过程中的直流电压和开关电流有关。
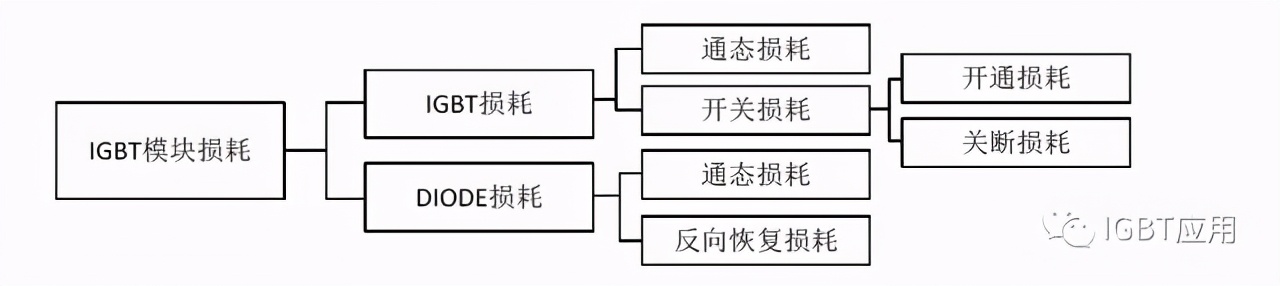
图 1 IGBT模块损耗构成
IGBT模块流过电流,产生一定的压降以及功率损耗,损耗计算公式就是压降和电流的乘积,如下式:
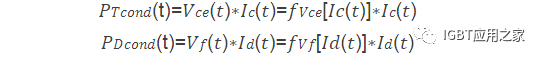
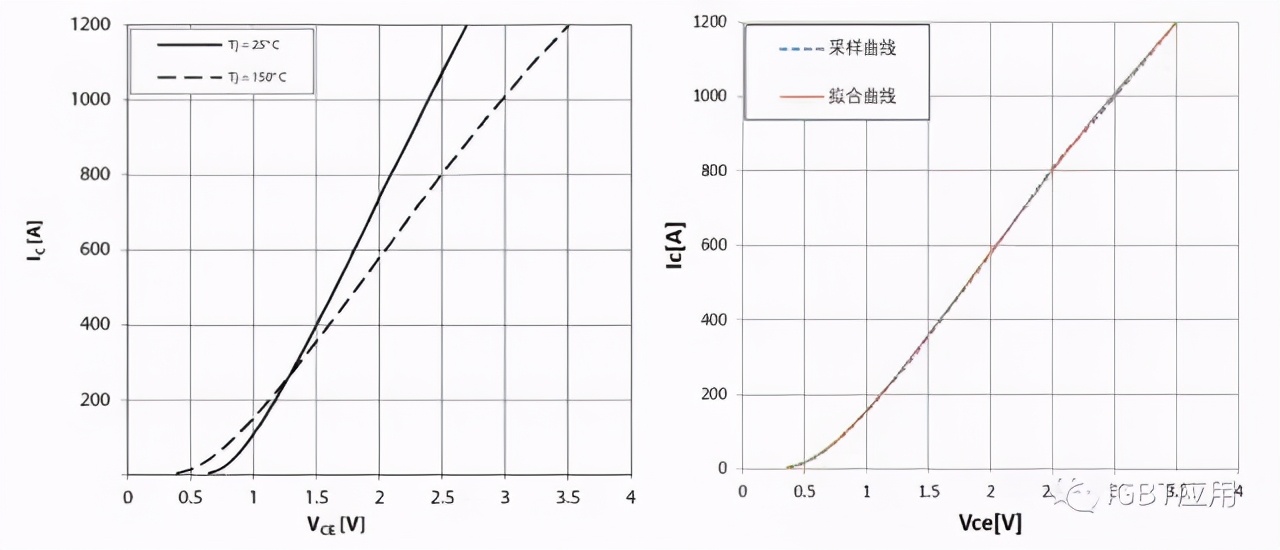
上式中,为()的函数(这里采用IGBT损耗计算来做说明,二极管类似),一般的,在规格书中可以找到二者的关系曲线,并可以看出是一种非线性关系。我们需要通过公式对该曲线进行描述才能进一步计算损耗。如果用线性方程来描述该曲线则会产生一定的误差。特别是计算电流小于额定电流点的时候,计算偏差可能会比较大。而通过高次多项式则可以较为准确的拟合该曲线,可以很好的消除计算偏差,得到一个准确的参数模型。下图为采用该公式拟合的曲线,可以看出和原曲线完美重合,效果非常好。
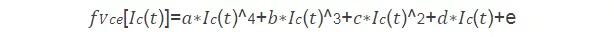
根据上式可以得到通态损耗的计算公式如下:
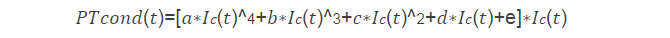
平均功率损耗则可以通过对一个工频周期积分求均值得到:
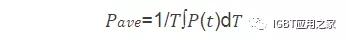
开关损耗并不是一个连续的量,对于每次开关,可以将损耗平均到整个开关周期。这样便可以得到近似连续的开关损耗的电流函数。开关损耗的大小除了跟开关电流有关,也受到直流电压的影响。因此可以得到开关损耗计算公式如下:
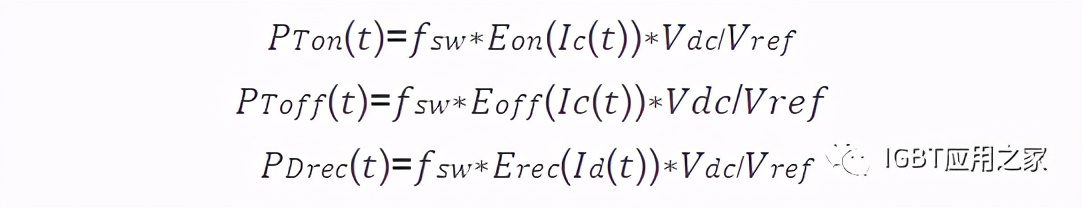
在规格书上可以找到电流对应开关损耗的关系曲线,我们采用高次多项式来描述同样可以得到如下的准确的损耗表达方式。开关损耗的线性拟合效果如下图所示。
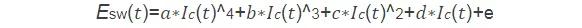
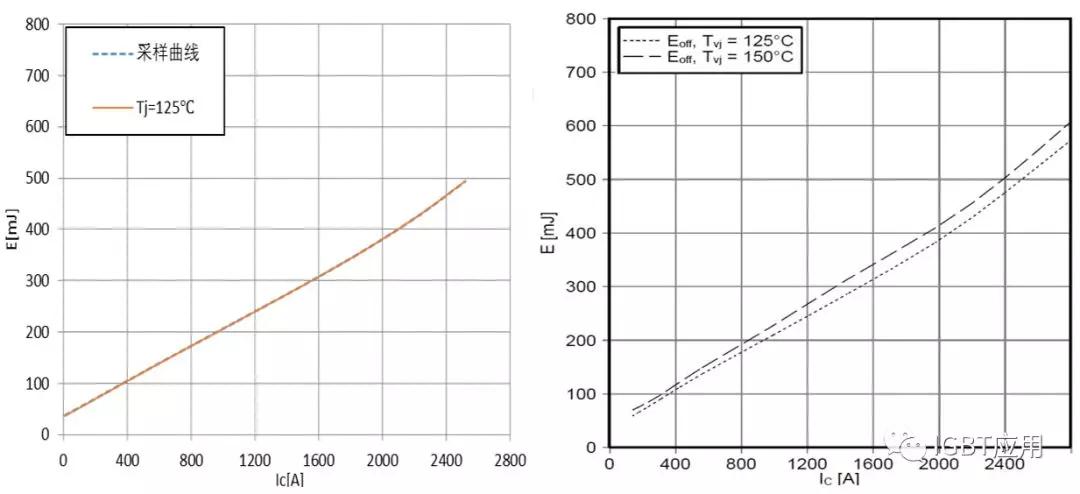
将上面的多项式带入开关损耗计算公式,下式为关损耗和反向恢复损耗的计算公式。
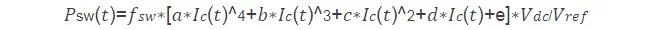

温度的影响
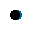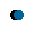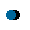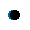
我们知道,在不同结温的时候,IGBT和DIODE的通态压降是不一样的。从上面图2中可以看出,结温在25℃和结温在125℃的时候,通态压降曲线相差挺大。传统的计算是在最终损耗的结果中加入一个经验值的修正因子。这样计算必然会引起一定的计算误差,因此我们需要在拟合公式中引入结温对通态压降的动态影响,如下式。
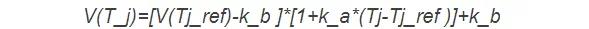
其中系数k_a和k_b是常系数,不同的器件数值会有不同,可以根据参数曲线中实际数值求得。下面两张图片分别为IGBT和DIODE的输出特征曲线应用该修正公式的实际修正结果。从图中可以看出,该公式可以很好的描述温度对通态压降的影响。
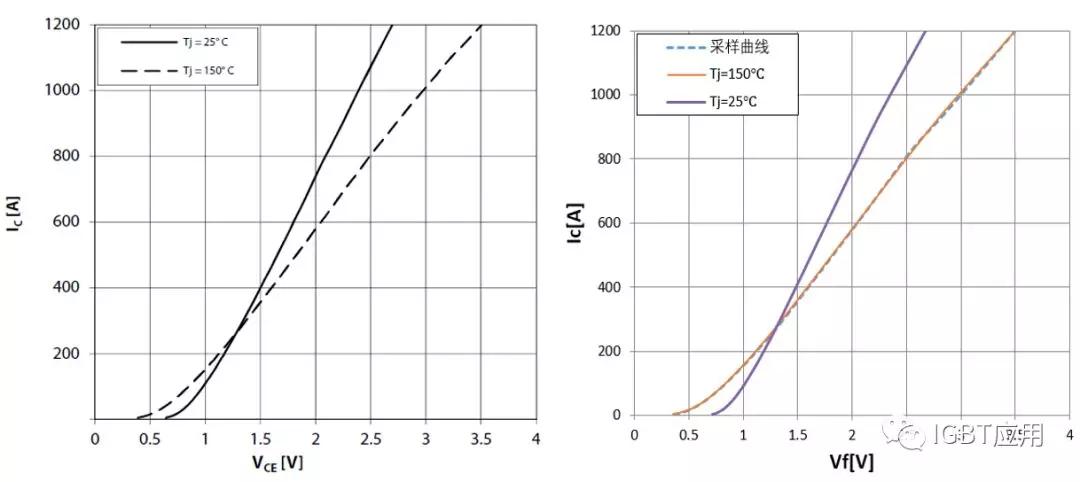
图4,对IGBT转移特性曲线的拟合和温度影响的修正结果对比
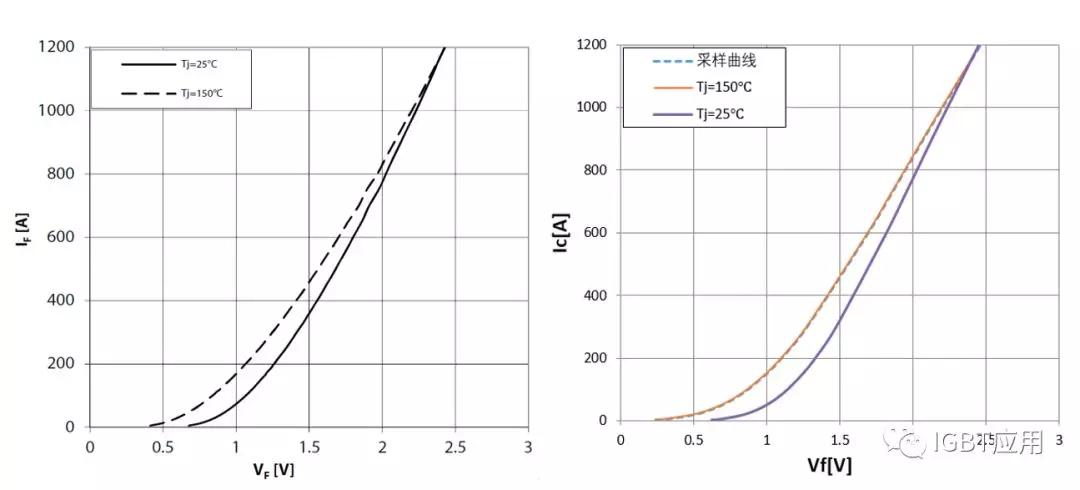
图5,对DIODE转移特性曲线的拟合和温度影响的修正结果对比
不仅仅通态压降受到结温的影响。开关损耗同样在不同结温条件下损耗也不同,结温变高开关损耗也会相应的增加。虽然厂家一般都会提供结温在125℃时的损耗,但是如果我们要追求更加精确的计算值,那就必须引入温度变量的影响,其效果如下图6所示。
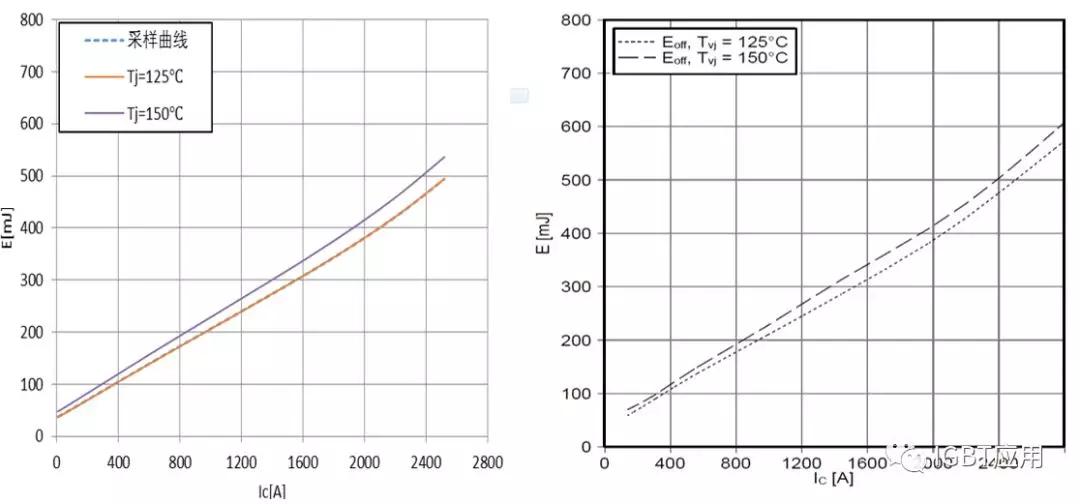
图6,关断损耗特性曲线的拟合和温度影响的修正结果对比
同时,由于结温变化对损耗的影响是一个反馈过程,因此在计算过程中也需要进行多次反馈迭代计算,直到稳态。

系统计算
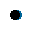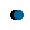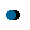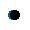
IGBT模块在系统中是通过PWM调制方式来使用的,也就是说器件中的电流是脉冲形式的。那么该如何计算在PWM调制情况下的损耗呢。如下图所示,为在调制模式下通过IGBT和二极管中的电流和分别的占空比(高脉冲代表IGBT导通,电流经过IGBT,低脉冲代表二极管导通,电流经过二极管)。考虑到输出端电感滤波器,电流一般是接近于正弦的。这样就可以得到每个开关时刻的开关损耗值。同样也可以得到导通损耗,但是由于IGBT和二极管是交替导通,这里需要考虑他们的占空比,也就是电流在开关管和续流管之间的分布。
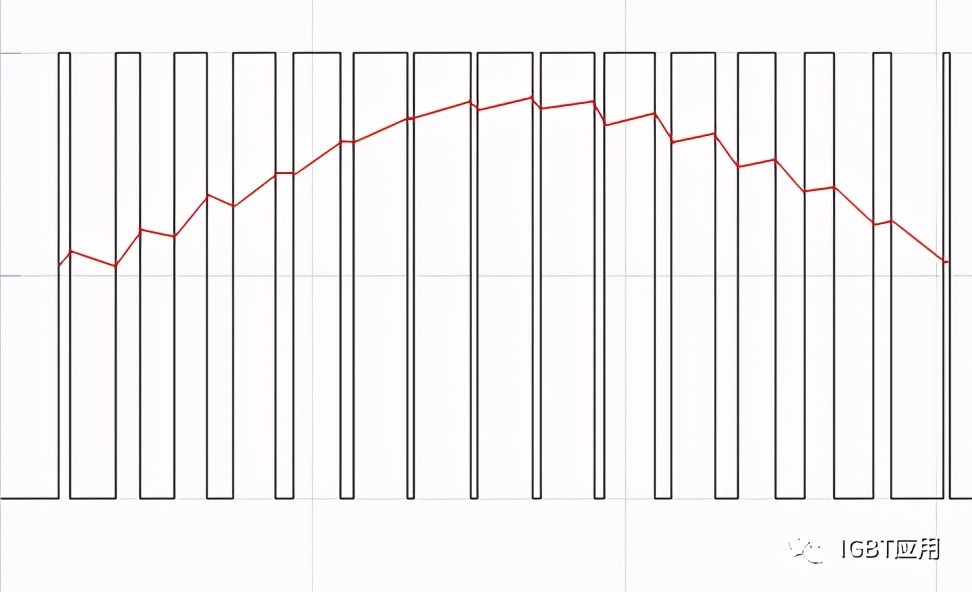
图 7,IGBT调制波和电流
我们知道,这里的占空比其实是由载波波形,通过三角波调制得到的,如下图 8。因此,可以得到如下占空比计算公式。
D=(sin(phi)+1)/2
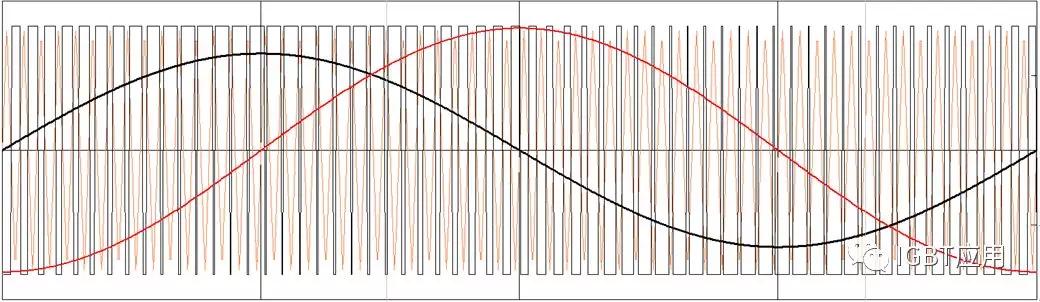
图 7,两电平双极性PWM调制波形和电压电流(黑色线:电压;红色线:电流)
这样在计算导通损耗的时候引入占空比就可以得到下面的计算公式。对于对应的续流器件,占空比则是(1-D)。
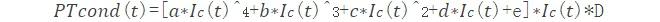
这样我们就得到了基本的计算公式,下面就需要考虑在拓扑结构中器件是如何工作,损耗是如何计算的。
对于两电平拓扑,计算损耗总共有两种模式:
1,上管IGBT导通电流,下管二极管续流,电流流出;
2,下管IGBT导通电流,上管二极管续流,电流流入,如下图:
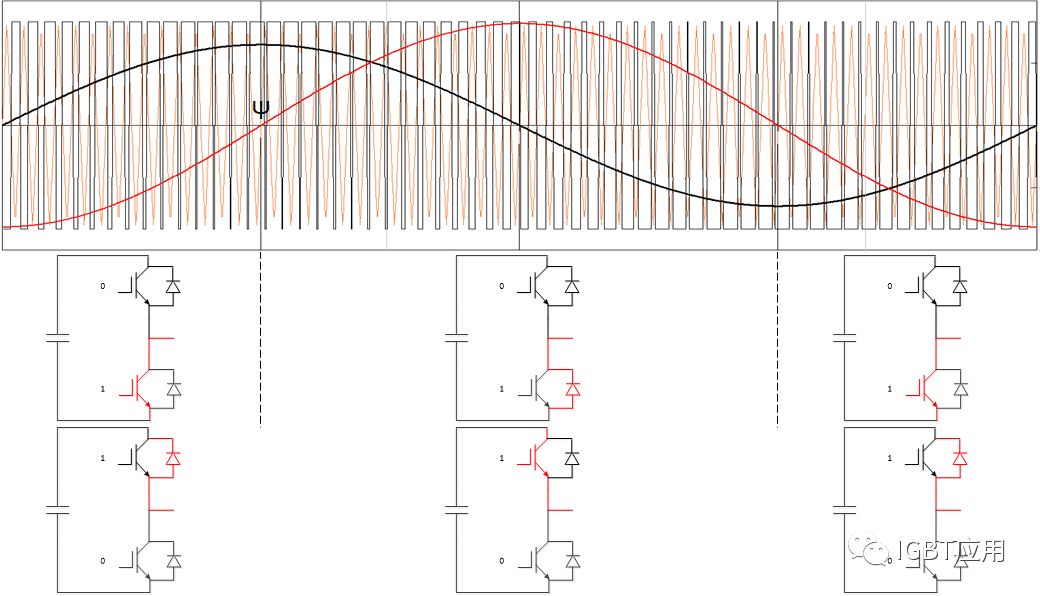
图 8,两电平开关以及电流路径模式
因此,当我们考虑计算上管IGBT损耗的时候,需要考虑到,上管IGBT只在区间(ψ,ψ+π)之间有损耗发生。考虑到占空比以及上面的计算公式,我们可以得到上管IGBT导通损耗的计算公式如下:
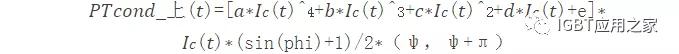
以及同理,下管IGBT的导通损耗公式:
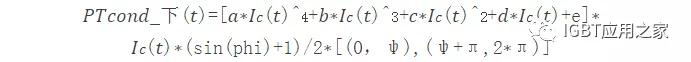
将上面的公式高次公式简化成一次线性函数并进行积分求平均,即可得到经常能看到的IGBT损耗的计算公式:
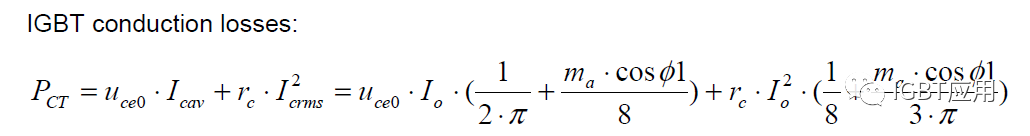
我们前面已经提到引入温度的影响,因此需要在上述公式中带入温度对通态压降的影响系数,得到公式如下(以上管IGBT为例):
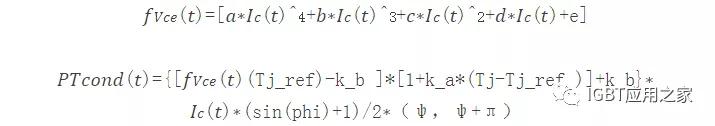
此外,k_b,k_a为温度对正向压降影响的系数。
同理对于关断损耗,也可以得到引入温度影响的损耗计算公式如下:
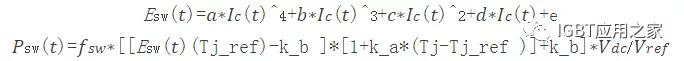
k_b,k_a为温度对正向压降影响的系数。
需要注意的是,/ 实际上,该比值往往不是简单的单位比例关系,且该值也对计算结果有着较大的影响。
二极管的损耗计算过程和方法类似,此处不再列出。
三电平系统的计算过程和方法也类似,只不过每个器件的工作周期不同,而且占空比的计算方式也有差异。但是原理相同,这里就不再详细推导列出。
该内容是小编转载自网络,仅供学习交流使用,如有侵权,请联系删除。







 /5
/5 

