- 散列函数:一个把查找表中的关键字映射成该关键字对应的地址的函数,记为Hash(key)=Addr(这里的地址可以是数组下标、索引或内存地址等)
散列函数可能会把两个或两个以上的不同关键字映射到同一地址,称这种情况为冲突,这些发生碰撞的不同关键字称为同义词。
- 散列表:根据关键字而直接进行访问的数据结构。
- 理想情况下,对散列表进行查找的时间复杂度O(1),即与表中元素的个数无关。
散列表的构造方法
- 直接定址法:直接取关键字的某个线性函数值为散列地址,散列函数为H(key)=key或H(key)=a*key+b
它适合关键字的分布基本连续的情况,若关键字分布不连续,空位较多,则会造成存储空间的浪费。
- 除留余数法:这是最常用的方法。假定散列表表长为m,取一个不大于m但最接近或等于m的质数p,利用公式:散列函数为H(key)=key%p 把关键字转换成散列地址。(用质数取模,分布更均匀,冲突更少)
- 数字分析法:设关键字是r进制数,而r个数码在各位上出现的频率不一定相同,可能在某些位上分布均匀一些,每种数码出现的机会均等;而在某些位上分布不均匀,只有某几种数码经常出现,此时应选取数码分布比较均匀的若干位作为散列地址。这种方法适合于已知的关键字集合,若更换了关键字,则需要重新构造新的散列函数。
- 平方取中法:取关键字的平方值的中间几位作为散列地址,具体取多少位要视实际情况而定。
处理冲突的方法
开放地址法: 所谓开放地址法,是指可存放新表项的空闲地址既向它的同义词表项开放,又想它的非同义次表项开放。Hi=(H(key)+di)%m
- 线性探测法:冲突发生时,顺序查看表中下一个单元,直到找出一个空闲单元或查遍全表。缺点:会造成大量元素在相邻的散列地址上“聚集”(或堆积)起来,大大降低了查找效率。
- 平方探测法:当di=0^2 , 1^2, -1^2,… , k^2, -k^2时,称为平方探测法,其中k<=m/2,散列表长度m必须是一个可以表示成4k+3的素数,又称二次探测法。可以避免出现“堆积”问题,他的缺点是不能探测到散列表上的所有单元,但至少能探测到一半单元。
- 伪随机序列法:当di=伪随机数序列时,称为伪随机序列法。
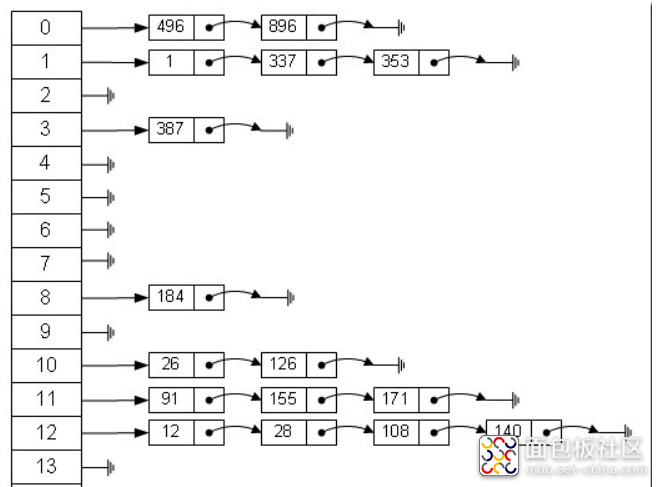
拉链法:把所有的同义词存储在一个线性链表中。






 /5
/5 


