一理论基础
当两个电路彼此靠近时,由于电路之间的电容性(电场)和电感性(磁场)耦合,在一个电路中传播的信号会在另一电路中感应出信号。这种现象称为串扰。基础模型如图1所示。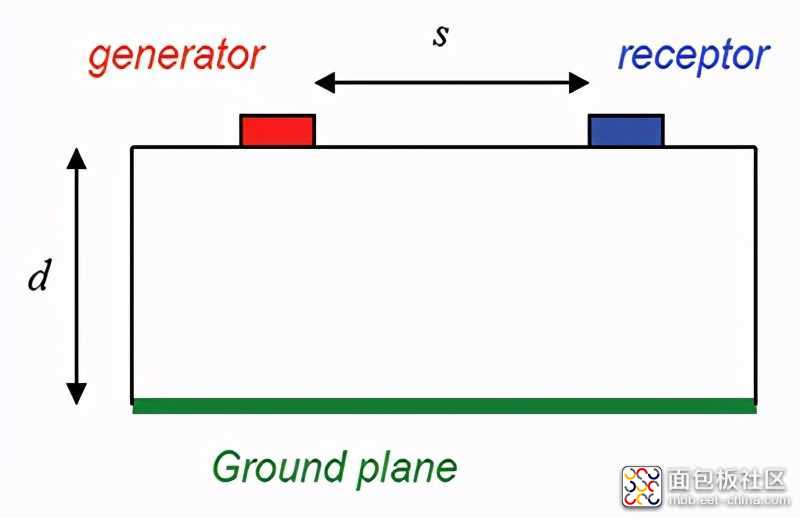
图1 微带线PCB示意图
两条微带线彼此之间距离为s,与接地层(信号返回平面)之间的距离为d。第一条走线(发射端)连接幅值为VS,内阻为RS的可变电压源,并端接阻值为RL的负载电阻。第二条走线(接收端),近端和远端分别接阻值为RNE和RFE的负载电阻。图2所示为对上述电路布置的建模。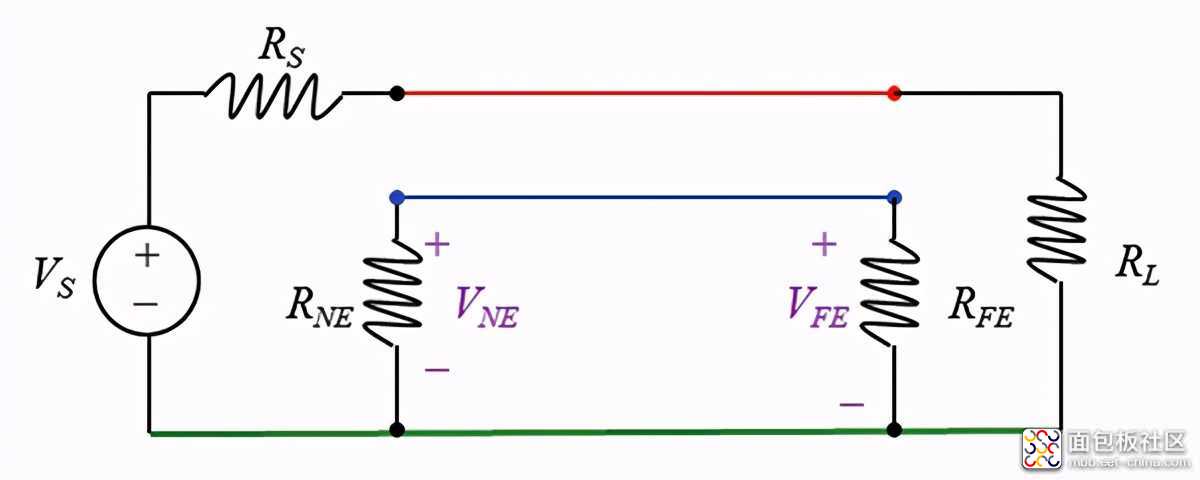
图2 微带线PCB电路模型
发射端线路上的交变电流IG产生磁场,该磁场引起的磁通量穿透在两导体的环路之间,从而在接收电路中感应出电压。我们通过互感LGR对此建模,如图3所示。
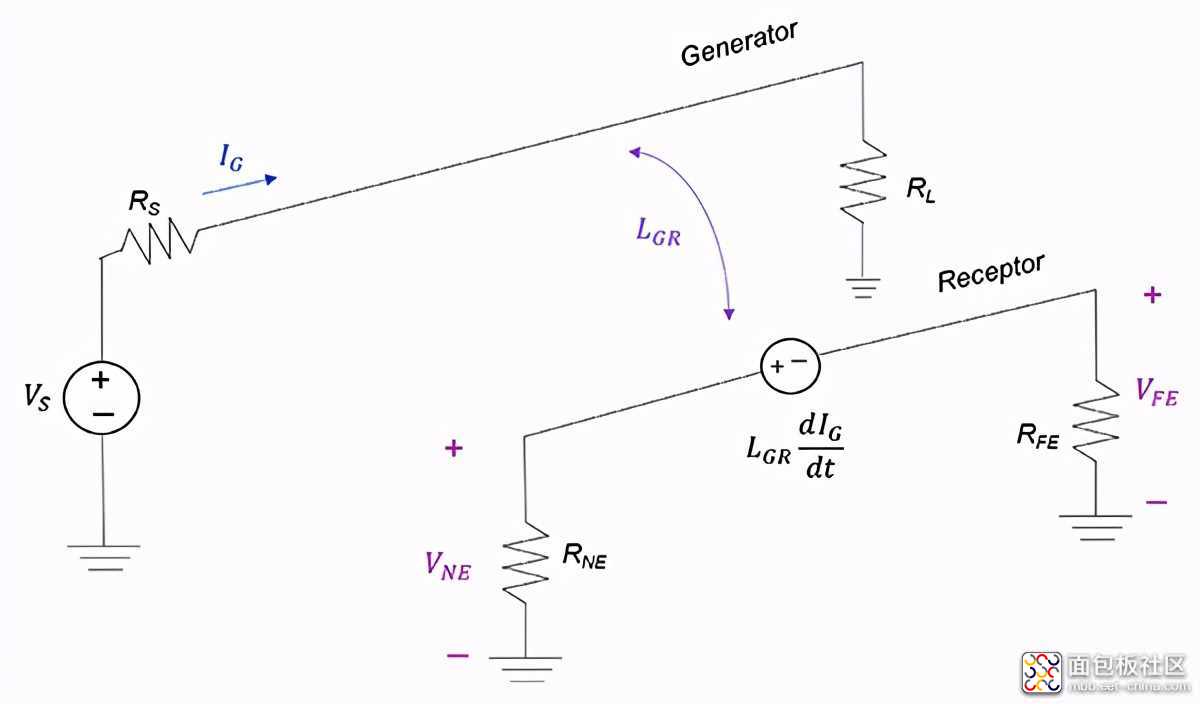
图3 电感耦合电路模型
类似地,发射端线路的交变电压VG在接收端线路上产生电场),从而在接收器电路中感应出电流。我们通过互容CGR对此建模,如图4所示。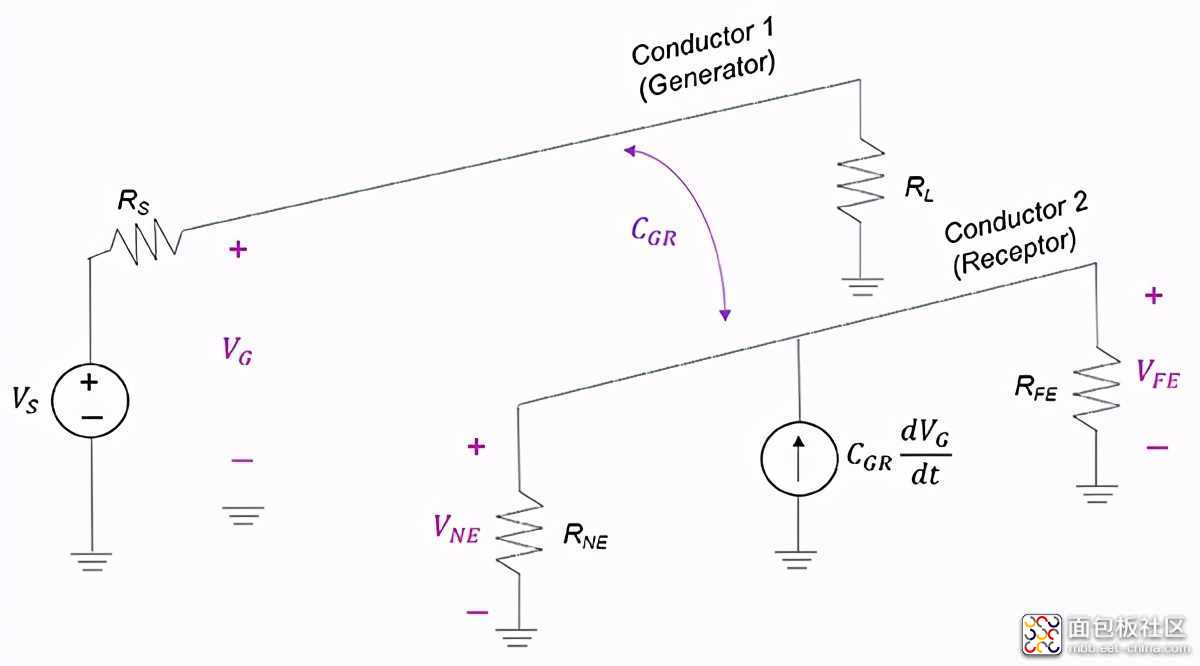
图4 电容耦合电路模型
两种耦合机制的叠加可用如图5所示电路等效。
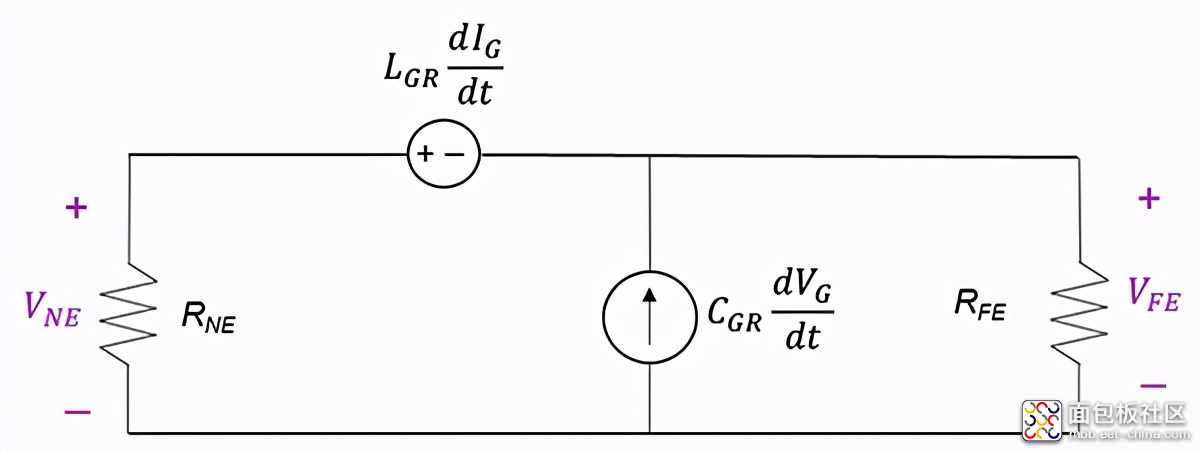
图5 接收器电路模型
通过叠加,近端和远端电压由下式给出:
(1a)
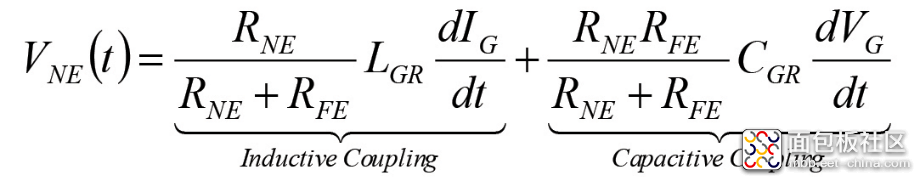
(1b)
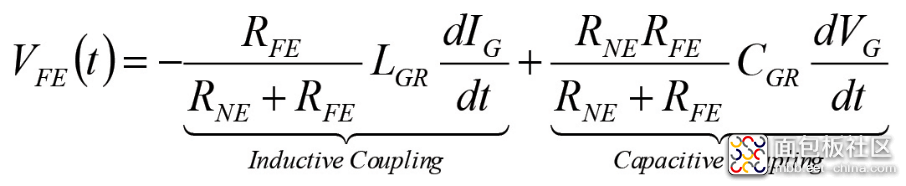
在假设线路在VS(t)的最高有效频率分量上短路的情况下,发射端线路上的电压和电流基本恒定。从而得出,
(2a)
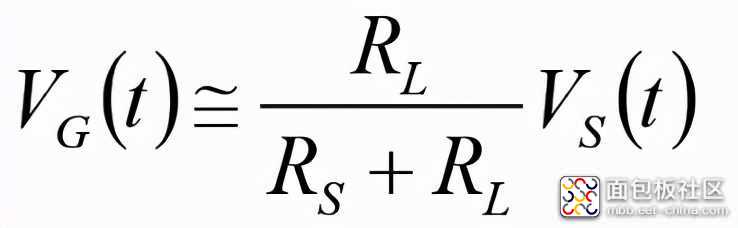
(2b)
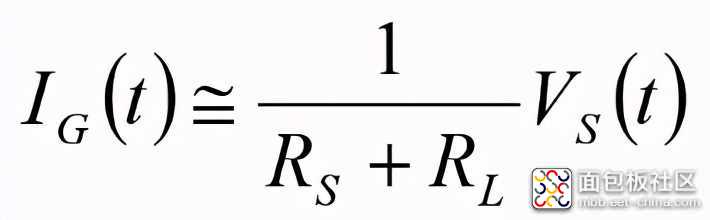
因此,
(3a)
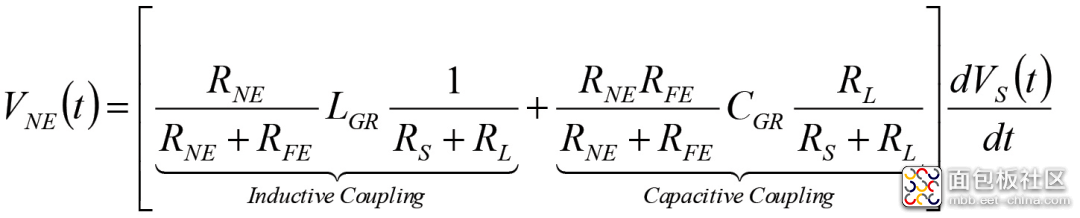
(3b)
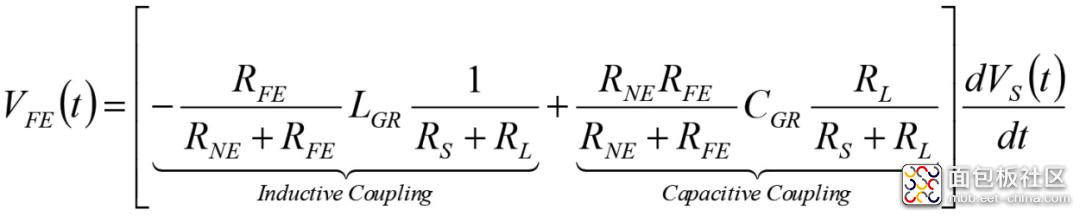
因此从上述公式我们可知,为了最小化串扰,我们可以减少:1)源信号Vs的变化,2)电感耦合LGR,或3)电容耦合CGR。
二验证结果
为了验证上述结论,我们做了如下实验,实验布置如图6所示。

图6 实验布置
图7为具有不同电路拓扑的PCB。

图7 具有不同电路拓扑的PCB
研究三种不同的电路拓扑,如表1所描述。
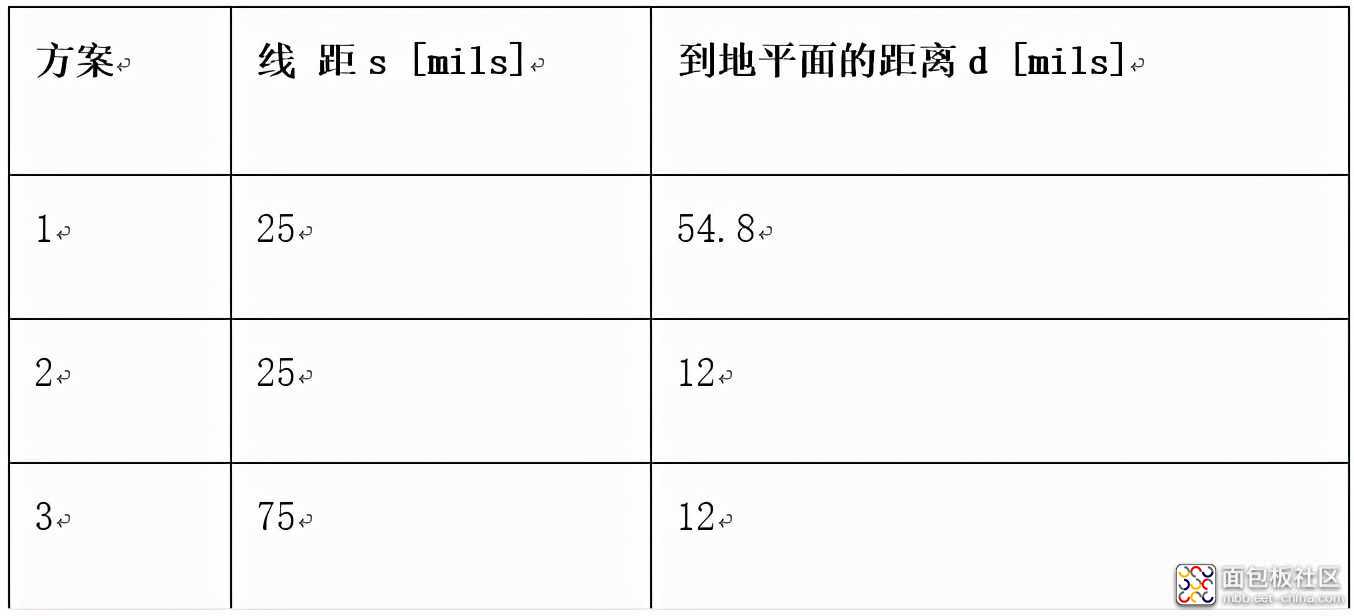
表1 电路拓扑
图8至图10显示了发射端(干扰源)信号,以及在接收端(敏感源)信号线上感应到的近端和远端电压。
该信号源的开路电压为1Vpp,1 MHz梯形脉冲信号,其上升时间为100 ns,下降时间为200 ns,占空比为50%。我们在方案1中进行以下观察,如图8所示。
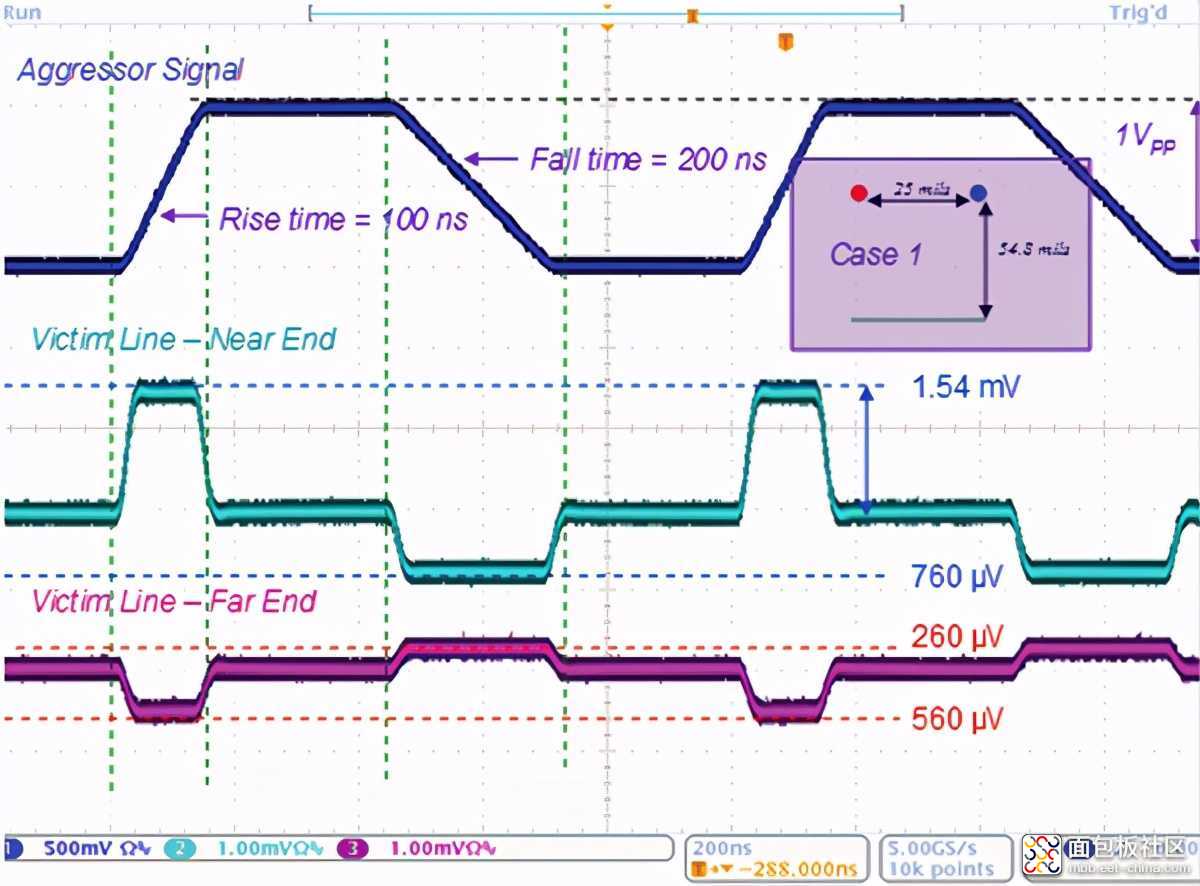
图8 串扰感应电压-方案1
对于近端感应电压,由于上升时间是下降时间的两倍,根据公式3a,感应电压的大小应相差两倍,实测与理论相符。我们还注意到,这两个电压的极性相反,这也可从公式3a得出。对于远端感应电压可以进行类似的观察。此外,由于近端电压的耦合系数(参考公式3a)为正,因此在上升期间的感应电压也为正。远端电压在上升时间内为负,表明电感性耦合相对于容性耦合为主要耦合方式(参见公式3b)。
方案2:使接地层靠近线路,同时保持线路之间的距离不变,主要减少了电感耦合并导致了感应电压幅值的减小,实测如图9所示。
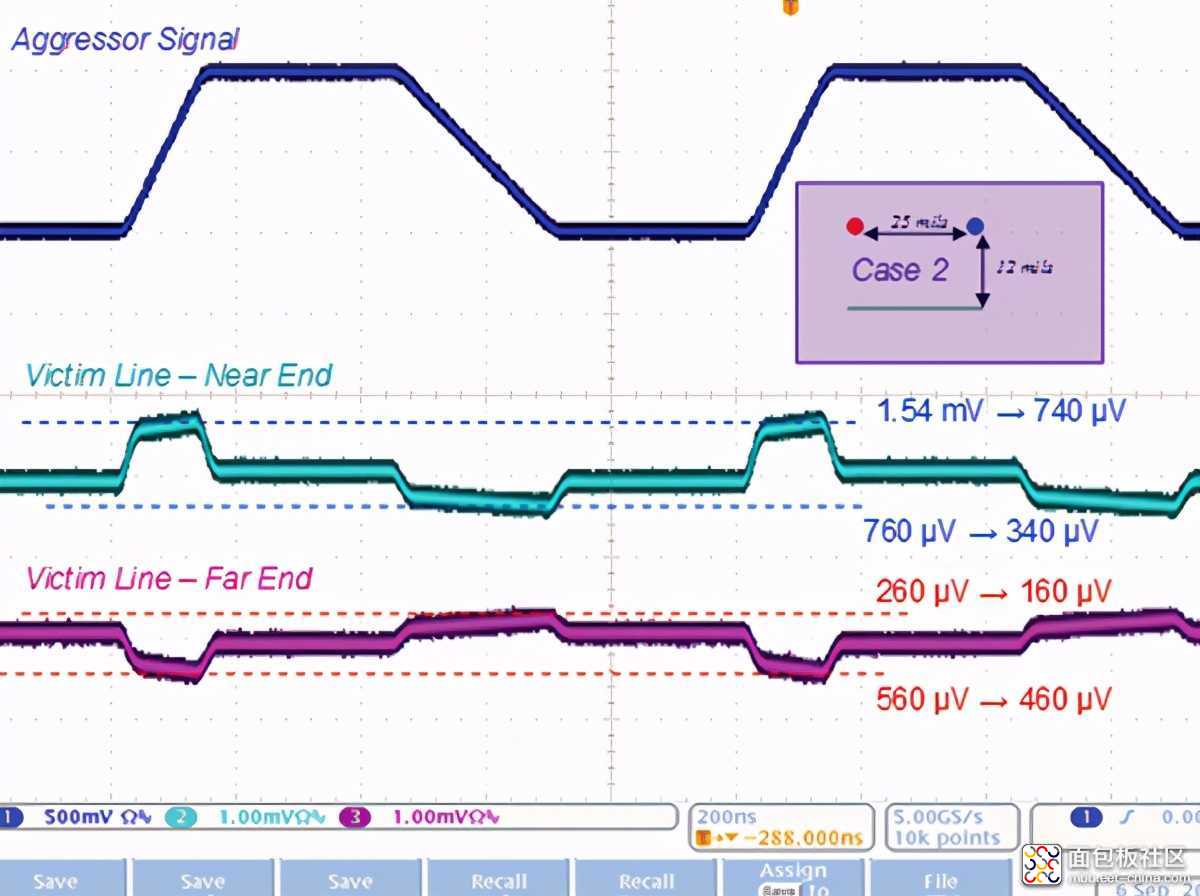
图9 串扰感应电压-情况2
方案3描述了与方案2到地平面的距离不变的情况,但是线之间的距离增加了。如图10所示,这主要减少了电容耦合,并进一步降低了感应电压。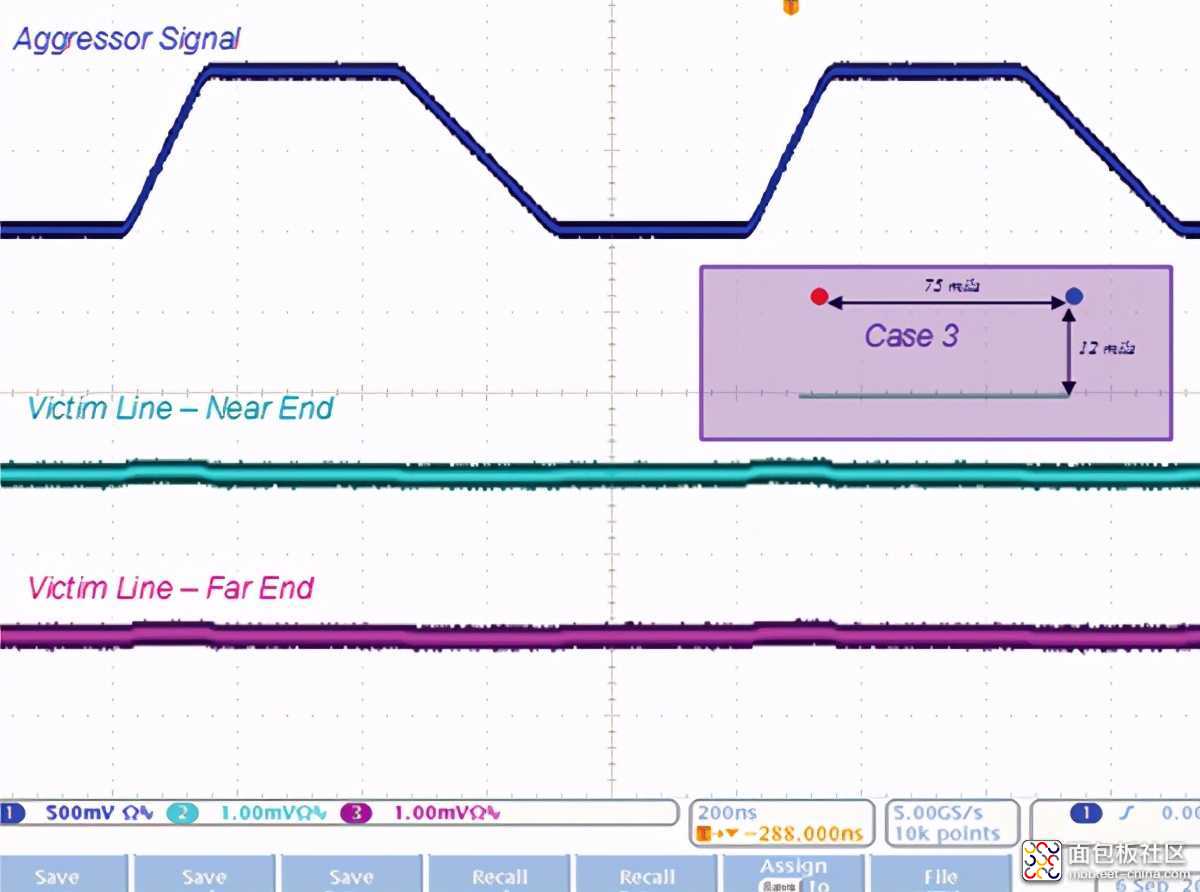
图10 串扰感应电压-情况3
串扰不仅影响信号完整性,同时增加电磁兼容风险,因此在PCB设计过程中要时刻注意关键信号走线方式,避免额外的噪声串扰。来源:韬略科技EMC







 /5
/5 

