开关电容(SC)采样电路是诸如Sigma-Delta ADC，SAR ADC等各种广泛应用的ADC中必不可少的电路模块，其负责对输入信号进行采样再交由ADC对采样电压进行模数转换。由于其处于ADC的关键路径上，因此常常容易造成采样误差，非线性等问题。要理解这些问题，首先需要清楚SC采样的具体过程，本文将SC采样的过程分为两个阶段，并从这两个阶段分析SC对开关导通电阻的要求。

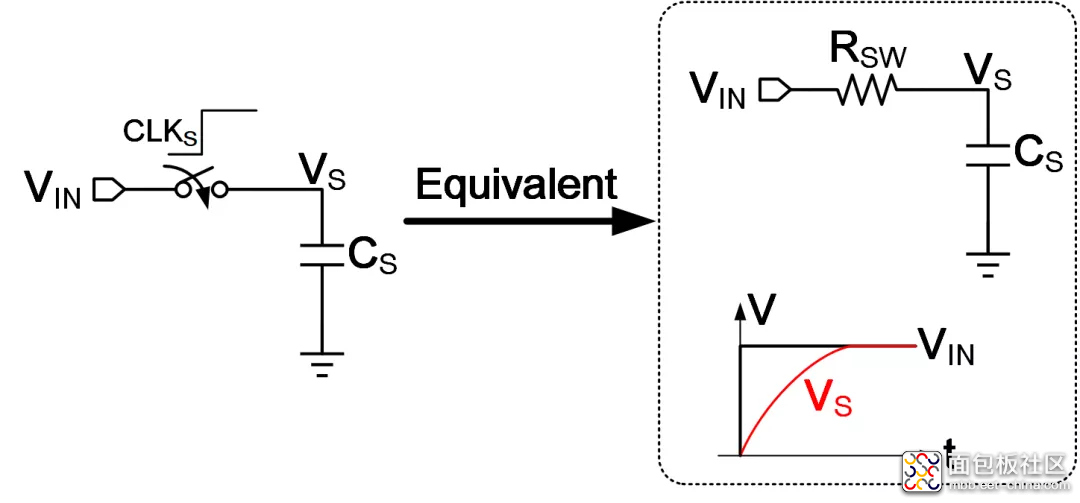
如上图所示，假设VIN为一个固定电平，在开关导通的一瞬间，采样电容CS上的电压变化等效为一个一阶RC阶跃响应，CS上电压可以表示为式(1):

其中，τ为时间常数：τ=RSWCS。

对于固定的采样时间t，为了使得VS与VIN的误差足够小，应该设计开关导通电阻RSW足够小。

可能有读者会质疑，即使RSW不够小，最终引起的VS与VIN之间也只是一个1-e-t/τ的增益误差。然而，这是建立在RSW是一个固定值的前提下，实际上对常用的CMOS，NMOS，PMOS开关而言，RSW会随着输入发生变化，因此1-e-t/τ也是变化的，这样它便无法被看作是一个固定不变的增益误差。因此，最稳妥的方式还是让e-t/τ在RSW变化的范围内足够小。

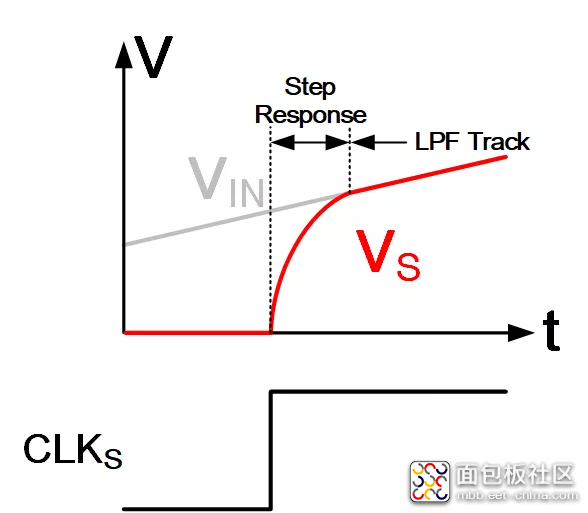
在上一节中，我们假设输入VIN是一个固定不变的直流信号，从而采样过程仅需要完成阶跃响应即可。然而，该假设仅在一部分应用中成立，如仪表测量，传感器测量领域。还有很大一部分应用下VIN为交流信号。这样的情况下，在阶跃响应阶段完成后，即VS等于VIN后，VIN还会继续变化，该情况下的采样过程如图2所示。

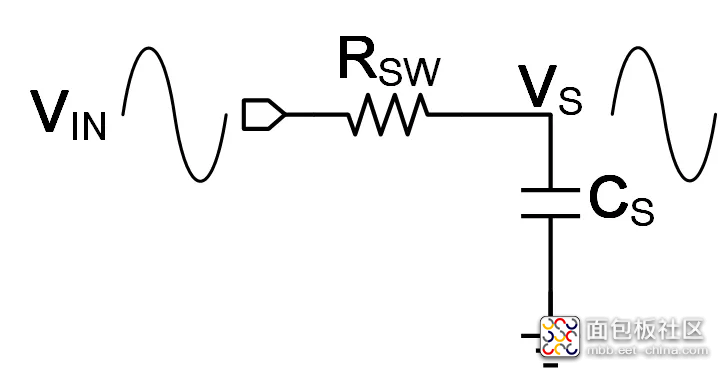
阶跃响应完成后，开关导通电阻RSW和采样电容CS形成了一个低通滤波器，输入信号在经过低通滤波后被采样电容上的电压进行跟随，这一过程等效模型如图3所示，其传递函数为式(2):

将式(3)分解为幅度和相位的变化可以表示为式(3)与式(4):

式(3)和式(4)表示该低通滤波器的输出的幅度和相位均受RSW影响。对常用的CMOS开关，NMOS开关和PMOS开关，由于RSW均会随着输入幅度变化，因此滤波器响应的幅值和相位都随着输入信号幅度变化而变，从而造成非线性。

通常有两种方式降低这一过程的非线性：

• 第一种是让RSW在所有情况下都足够小，以确保在所关心的频率范围内ωRSWCS足够小，这样根据式(3)和式(4)，在所关心的频率范围内，幅度响应尽可能为1，相位响应尽可能为0°，便不会引起非线性。在电路设计时，会通过提高开关的宽长比来实现减小RSW的目的。
  
• 另一种方式是让RSW不随输入幅值变化，这样虽然输出和输入之间存在幅值差和相位差，但幅值差和相位差是固定的，因此不会引起非线性，一些开关恒定VGS技术便是为了实现这样的目的。
  

正如上文所言，对于直流信号采集的应用，通常只需要考虑阶跃响应阶段的影响，确保开关阻值足够小以使得采样电容上电压可以建立在要求的误差范围内即可。或者也可以认为，直流信号本身是频率ω很小的情况，因此根据式(3)和式(4)，滤波器在这样小的频率ω下很容易实现幅度响应约为1，相位响应约为0°，因此不会存在非线性。

而对于交流信号，阶跃响应阶段和低通滤波器跟随阶段均需要考虑，电阻阻值需要满足两个阶段的要求。然而，究竟哪个阶段对电阻阻值要求更为严苛，则和采样频率，信号频率息息相关，而这两者之间的关系又因为过采样技术的使用变得多样，因此在实际设计时，最佳方案还是两者都进行分析，并留够充足的设计裕度。