递推算法与递推套路(算法基础篇)
相信了解算法同学经常会说动态规划太难了,看到题目完全不知从何下手,或者是说“一看题解就会,一看题目就废”这样的一个状态。本质上是由于学习动态规划的时候,学习方法不对,最终导致南辕北辙,没有掌握其中精髓。而动态规划与递推算法又有着暧昧不清的关系,我们选择先从递推算法入手,一步一步揭开动态规划的神秘面纱。
作者/ 汤文辉
编辑/ 黄倩倩(实习)
一、递推公式
每一个递推算法,都有一个递推公式,通过递推公式我们可以更加明确的了解递推算法。
1.1 斐波那契数列的递推公式
f(n) = f(n-1) + f(n-2),这是我们斐波那契数列的递推公式,有很多同学可能会问,这个公式实际有什么用呢?接下来,我们来直接看一个算法题:爬楼梯。
LeetCode 70. 爬楼梯
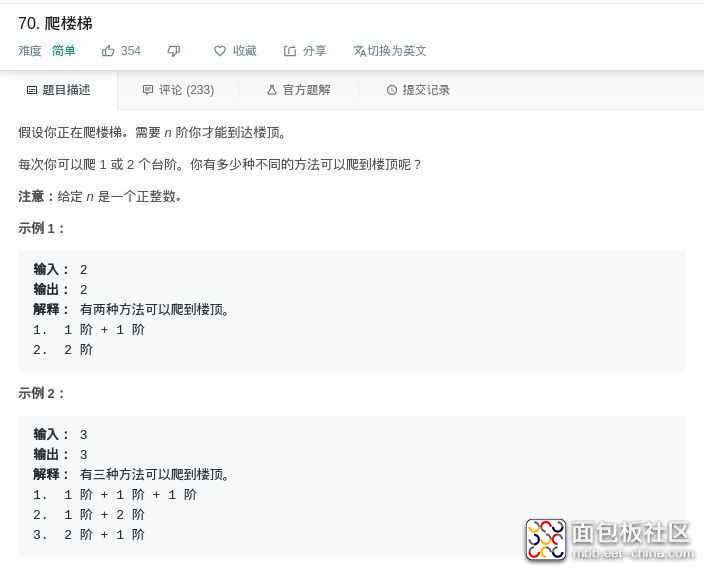
这道题我们要怎么理解呢?我们如果想要爬到第 n 阶楼梯,那么上一步有可能是在 n-1,也有可能是在 n-2。

因此,这道题的解法就一目了然了:
function climbStairs(n: number): number { const res: number[] = []; // 爬到第0层的方法就是一动不动,我们可以认为他只有一种 res[0] = 1; // 爬上第一层阶梯的可能性只有1个,就是走一步 res[1] = 1; // 因此,后面的爬楼方式,我们就可以通过地推方式计算出来 for(let i=2;i<=n;i++) { res[i] = res[i-1] + res[i-2]; } return res[n]; };
复制代码二、数学归纳法
上面带着大家一起学习了一下斐波那契数列递推公式的实际应用。那么,为什么上面这个公式就能够描述这一类问题的特性呢?这就要再聊一下数学归纳法了。
数学归纳法在整个计算机科学当中是非常重要的,主要分为以下几步:
1.验证 k0成立(边界条件);
2.证明如果 k(i) 成立,那么 k(i+1) 也成立;
3.联合步骤1和步骤2,证明由 k0~k(n) 成立。
不知道大家是否还记得,之前我们学习二叉树时,有扩展学习过递归程序的设计,而递归程序的设计要点就是数学归纳法在广义方面的应用,又称为结构归纳法。那么,我们再来看一下上面的爬楼梯问题,怎么使用数学归纳法分析。
1.验证 k0 成立:在爬楼梯问题中,我们的边界条件就是当 n 为 0和n为1。
2.证明如果 k(i) 成立,那么 k(i+1) 也成立:我们假设 res[i-1] 和res[i-2] 是正确的,那么,res 也是成立的。
3.联合步骤1和步骤2,证明由 k0~k(n) 成立:由于步骤1和步骤2联立,必然能够得出 res[n] 是成立的。
三、如何求解递推问题
论求解套路的重要性:求解套路就是递推算法的学习方式,如果学习方式错了,很可能南辕北辙,花了比别人更多的时间,反而掌握的更少。就像健身的时候,如果你掌握了一些动作要领,可能1~2个月肌肉就出来了,但是你要是没有掌握动作要领,练错了,不仅长得肌肉变成肥膘,还可能伤到自己。
1.确定递推状态(重点)
-一种函数符号 f(x) 以及赋予函数符号一个含义
例如上面的斐波那契数的求解问题,我们要赋予 f(x) 一个含义:爬上第x阶楼梯的方法总数。
-函数所对应的值就是我们要求解的答案
如:f(x) = y中,x 是自变量,y 是因变量。而在上面爬楼梯的问题当中,自变量x就是要爬的楼梯数,而因变量 y 就是爬到 x 阶楼梯的方法总数。因此,我们在求解问题的时候,最终要的是确定哪个是自变量,哪个是因变量。通常,因变量的值就是我们要求解的值。
那么,我们要如何分析题目中的自变量是什么呢?我们要确定,会影响因变量的因素有哪些。如爬楼梯问题中,影响方法总数的就只有我们当前要爬的楼梯数,因此,自变量就是楼梯数 x。
-思维练习

首先来分析一下递推状态是什么:
首先第一个会影响我们方法总数的自变量就是 n,即房间被划分成了几个区块,其次,由于房间是环形的,为了不让首尾颜色相同,我们还需要将首尾颜色也记录到我们的递推状态当中,那么,我们就得到了如下的公式:
f(n, i, j) = y,其中,n 代表一个房间被分成几个区块,i 和 j 分别代表首尾颜色,y 代表方法总数。
这个公式的意思是:总共有 n 个区块的房间,第一个区块涂第 i 种颜色,最后一个区块涂第 j 种颜色并且相邻颜色不同的方法总数为 y。
-递推公式
上面分析得出了 f(n, i, j) = y 这样一个简易版的公式,现在,我们就需要确定,通过怎样的运算能够算出f(n, i, j):
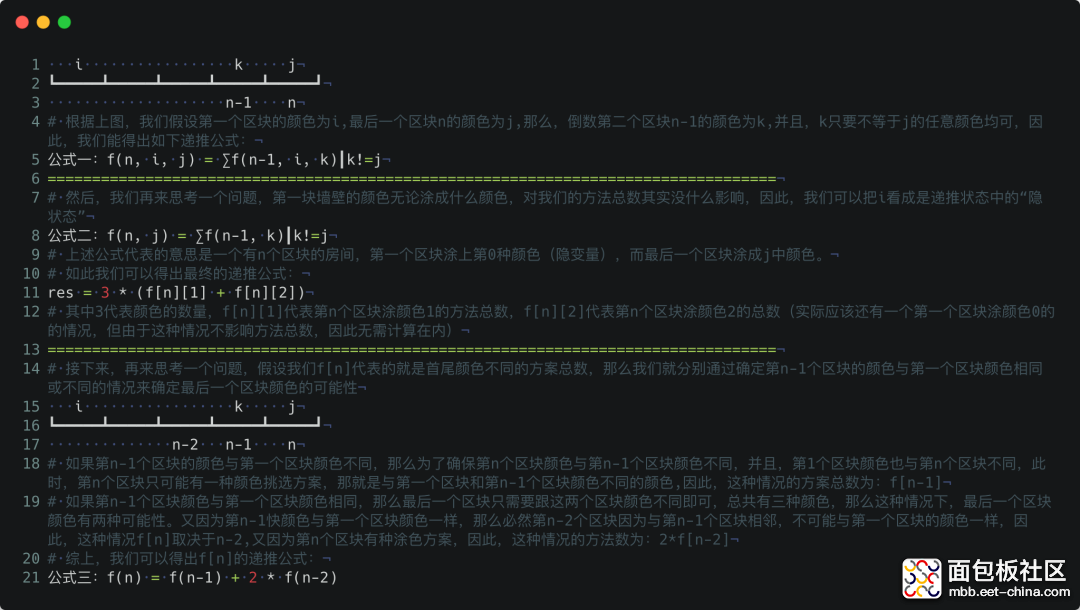
注意,上面三个递推公式都是正确的,只是在不断的优化我们的递推公式,提升程序效率,但三种方式都可以求解出正确答案。
2. 确定递推公式
-确定 f(n) 依赖于哪些 f(i) 的值
3. 分析边界条件 (k0)
4. 程序实现
-递归
-循环
四、递推与动态规划
动态规划问题其实就是求解最优化的递推问题,动态规划问题相较于普通的递推问题,多出了一个决策的过程。空讲概念有点抽象,我们来结合具体问题来分析。依旧还是爬楼梯问题,不过比之前的爬楼梯多了一个体力花费。
LeetCode 746. 使用最小花费爬楼梯

这道题与上面简单的爬楼梯问题类似,差别就在于每上一层楼梯,我们需要花费一定的体力,要求我们求出花费最小的体力。

通过上面的分析,我们可以得出以下公式:dp[n] = min(dp[n-2] + cost[n-2], dp[n-1] + cost[n-1])。
翻译一下上面的公式 :爬上第 n 层楼梯的总体力花费应该等于最后一步从第 n-2 层爬上来的体力花费与最后一步是从 n-1 层爬上来的体力花费的最小值。
function minCostClimbingStairs(cost: number[]): number { const n = cost.length; const dp: number[] = []; // 由于题目给定可以从第0层或第1层开始爬,因此,我们初始化第0层和第1层的体力花费为0 dp[0] = 0; dp[1] = 0; // 我们从第二层的体力花费开始递推 for(let i=2;i<=n;i++) { // 第i层的体力花费是我最后一步从i-1层爬上来的体力花费与从i-2层趴上来的体力花费的最小值 dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]); } return dp[n]; };
复制代码大家都觉得动态规划学起来很难,主要是因为我们要真正学好动态规划,需要从:递推状态定义、状态转移方程推导、程序实现等三个大方向上入手并学习,并且这三个方向都是不好学的。今天通过递推算法与递推公式的相关学习,以及初步的了解了递推算法与动态规划的关系。这些都是我们后续学习动态规划的基础,其中尤为重要的是数学归纳法的理解与应用。“光说不练假把式”,今天说的大部分都是理论,下一篇文章《递推算法与递推套路(手撕算法篇)》将会直接从一些递推或动态规划的题目入手,学习递推程序或动态规划程序的求解套路,让你看到递推和动规不再茫然。敬请期待!
递推算法与递推套路(手撕算法篇)
之前学习基础知识的时候也说了,递推和动态规划有这暧昧不清的关系,可以说,动态规划就是多了一个决策过程的递推。因此,我们今天的刷题也会涉及到一些比较简单的动态规划的题目,同样能够对我们深刻的理解递推算法起到帮助,也为我们之后深入学习动态规划算法和动态规划的优化打下基础。
作者/ 汤文辉
编辑/ 刘振宇
一、前置知识
1.1 滚动数组
使用场景:当我们下(上)一行的状态可以仅仅通过上(下)一行的信息推导出来,并要求我们求解最后(第)一行时,我们无需将每一行的数据都存储在数组当中,可以通过滚动数组的技巧,节省空间复杂度。
具体实现:假设我们已经知道第一行的数据,并且通过第一行数据经过一定的运算可以得到第二行的数据,那么,我们只需要一个数组临时存储两行数据,就可以将之后的每一行数据的结果计算出来,不断的滚动替换这两行数据,最终求解出最后一行数据的方式。
关键点:推导计算当前行和下(上)一行的索引。由于数组是滚动的,因此,我们目标行的索引也是随时变化的,以下为求取当前行和上(下)一行的通用公式:
当前行: const curIdx = i % 2由于我们的滚动数组只有2行,因此,当前索引只要与2求模即可; 上(下)一行:const preIdx = +!curIdx 由于滚动数组只有两行,索引要么是0,要么是1,我们对当前行取反便可得到上(下)一行的索引(注意,在js中,对1取反是false,对0取反是true,因此我们通过一个隐式类型转换将布尔类型转换为数字类型)。
复制代码二、刷题正餐
2.1 LeetCode 120. 三角形最小路径和

2.1.1 解题思路
按照我们之前将的递推套路:
1. 定义递推状态:在这道题中,我们每走一步的路径和主要取决于当前所处的行数i和当前的列数j,因此,我们这道题的递推状态应该是:dp[i, j]
2. 递推公式:确定了递推状态之后,我们就要确定递推公式了。那么,第i行第j列的数据要如何才能推导出来呢?首先,依据题意,我们要求最小路径和,如果我们从最底下往上走,那么我们可以知道,下一行i的数据应该是上一行i+1合法路径的最小值加上当前走到节点的值。
因此,我们得到了如下公式:
// 第i行第j列数据的推导公式dp[i, j] = min(dp[i+1, j], dp[i+1, j+1]) + val[i,j]
复制代码4. 程序实现:我们直接使用循环加滚动数组技巧实现。
2.1.2 代码演示
function minimumTotal(triangle: number[][]): number { const n = triangle.length; // 递推公式(状态转义方程)以下为自底向上走的公式 // dp[i, j] = min(dp[i+1, j], dp[i+1, j+1]) + val[i,j] // 由于i只跟i+1有关,因此,我们可以用滚动数组的技巧定义dp数组 let dp: number[][] = []; for(let i=0;i<2;i++){ dp.push([]); } // 首先初始化最后一行的数值,由于使用了滚动数组的技巧,因此,我们最后一行的索引应该是(n-1)%2 for(let i=0;i<n;i++) { dp[(n-1)%2][i] = triangle[n-1][i]; } // 然后从倒数第二行开始求值 for(let i = n-2;i>=0;--i) { // 由于使用了滚动数组,因此,当前行的下标为i%2,而下一行的下标则是当前行下标取反 let idx = i % 2; let nextIdx = +!idx; // 根据上面的公式计算出每一个位置上的值 for (let j=0; j <= i; j++) { dp[idx][j] = Math.min(dp[nextIdx][j], dp[nextIdx][j + 1]) + triangle[i][j]; } } // 最终,三角形顶点的那个值就是我们要求的值 return dp[0][0]; };
复制代码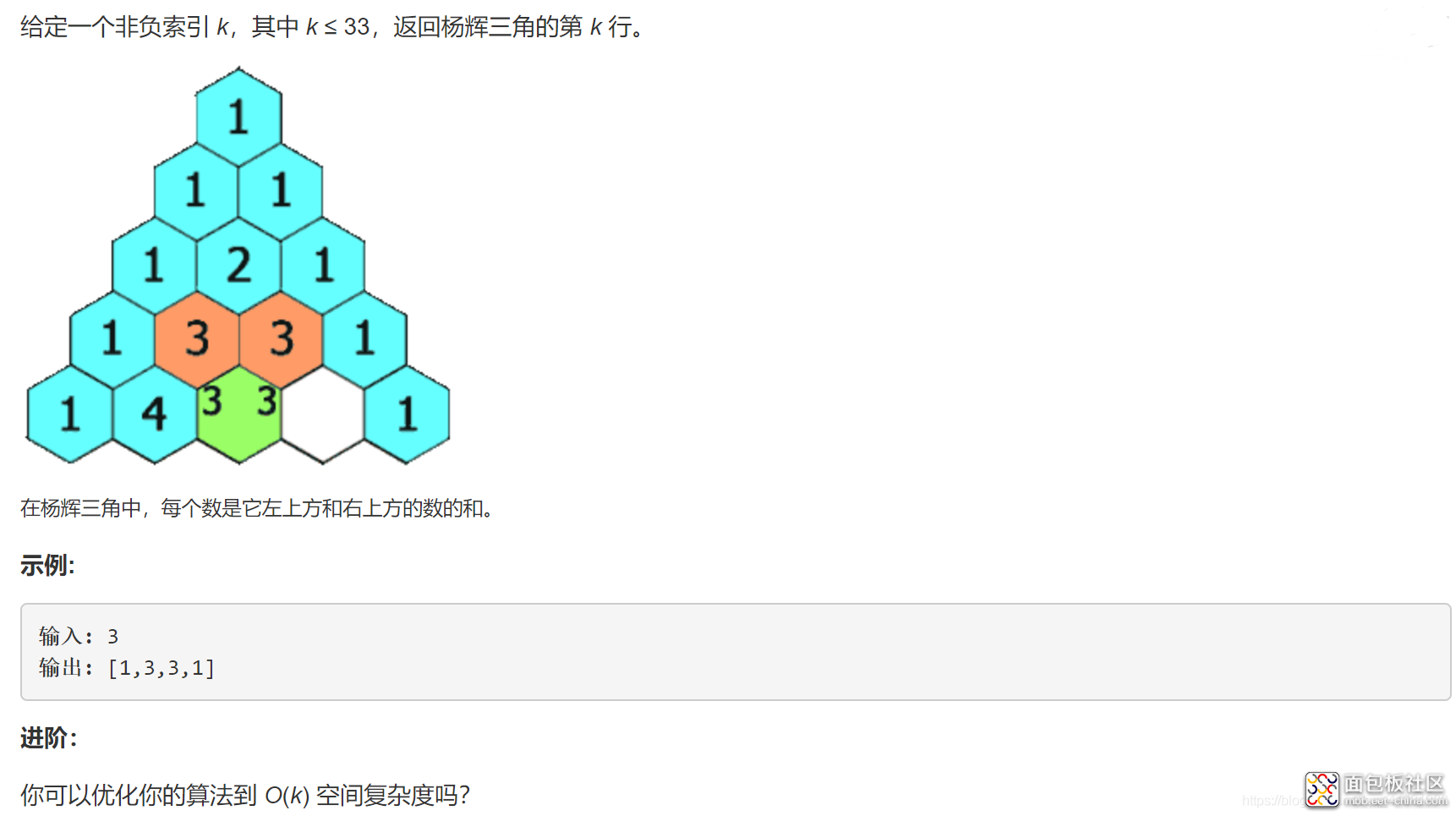
2.2.1 解题思路
这道题与上一道题类似,依然可以根据上一行推导出下一行的值,因此还是要祭出滚动数组的技巧,递推状态与递推公式的分析也比较类似,大家可以自己尝试推导。
而这一道题的边界条件,其实就是每一行的第一位都应该是1。
2.2.2 代码演示
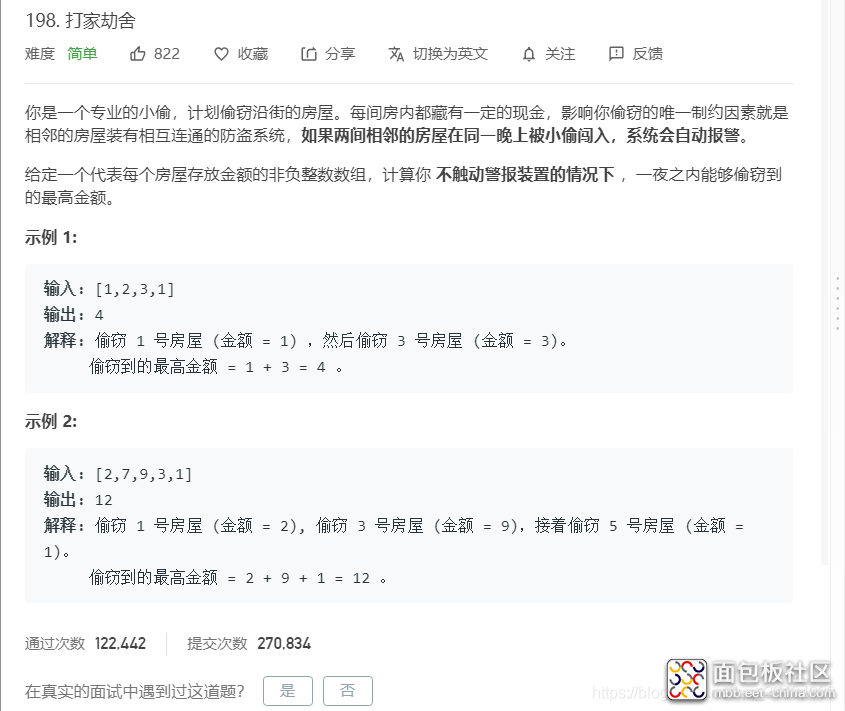
2.3.1 解题思路
1. 递推状态分析:既然要求能够偷到的最多的金额,那么,假设最后一家是n,那么,最大金额与我们是否偷最后一家有直接的关系,我们需要分类讨论:
a. 不偷最后一家:dp[n][0]其中,0代表不偷
b. 偷最后一家:dp[n][1]其中,1代表偷
2. 确定递推公式:由于递推状态分为两种情况讨论,因此,我们的递推公式,也应该分成两个部分:
a. 不偷最后一家:由于不能连续偷相邻的两家,如果最后一家不偷,那么,我们倒数第二家就可以偷,因此,此时我们的最大收益就取决于偷倒数第二家的金额与不偷倒数第二家金额的最大值。即:dp[n][0] = max(dp[n-1][0], dp[n-1][1])
b. 偷最后一家:由于要偷最后一家,那么就不能偷倒数第二家,因此,这种情况的最大收益是不偷倒数第二家获得的收益加上偷最后一家带来的收益,即dp[n][1] = dp[n-1][0] + nums[n]
3. 确定边界条件:
依据题意,我们如果不偷第一家的时候,因为一家都没偷,此时收益应该为0。如果偷第一家,那么收益就是第一家的钱。至此,我们就确立了最开始的边界条件。
4. 程序实现:这道题由于当前收益只取决于上一家的收益,因此依然使用滚动数组技巧加循环实现。
2.3.2 代码演示
function rob(nums: number[]): number { const n = nums.length; // 由于不能连续偷两家,因此,最大收益应该分为两种情况讨论: // 1. dp[n][0] = max(dp[n-1][0], dp[n-1][1]) 即:不偷最后一家的最后收益,取决于我偷倒数第二家的收益与不偷倒数第二家的收益的最大值 // 2. dp[n][1] = dp[n-1][0] + nums[n] 即:如果投了最后一家,那么倒数第二家就不能偷,所以最大收益就等于不偷倒数第二家的收益加上偷最后一家获得的收益 const dp: number[][] = []; for(let i=0;i<2;i++) dp.push([]); // 初始化第0家的值 dp[0][0] = 0;// 不偷第一家时收益为0 dp[0][1] = nums[0];// 偷第一家时收益为第一家的钱 for(let i=1;i<n;i++) { // 使用滚动数组技巧 let idx = i % 2; let preIdx = +!idx; dp[idx][0] = Math.max(dp[preIdx][0] , dp[preIdx][1]); dp[idx][1] = dp[preIdx][0] + nums[i]; } // 最终收益最大值时不偷最后一家和偷最后一家的最大值 return Math.max(dp[(n-1) % 2][0], dp[(n-1) % 2][1]); };
复制代码给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。

2.4.1 解题思路
1. 递推状态分析: 我们要求最大子数组的乘积,那么我们可以用 dp[n] 代表最后一位是 n 的最大子数组乘积最大值。
2. 递推公式: 最后一个数是 n 有两种可能性,第一种是让 n-1 的最大乘积再乘上当前n的值,第二种则是 n 不与之前的值相乘,自开一国,因此,我们应该在这两种情况中选一个最大值,所以,递推公式应为: dp[n] = max(dp[n-1] * val[n], val[n])
3. 边界条件: 由于数组中可能含有负数,有可能使当前值乘上原先的最大值变成最小值,也可能时当前值乘上原先的最小值变成最大值,因此,我们不仅需要记录当前数字之前的最大值,也要记录最小值,方便处理负数的情况。而初始时,由于我们要求的是乘积关系,那么我们的最大值和最小值都初始化为1即可。
4. 程序实现: 由于第 n 项的最大乘积只跟 n-1 有关,我们可以使用变量方式存储关系,不需要额外开辟递推数组空间。
2.4.2 代码演示
function maxProduct(nums: number[]): number { // 递推状态:dp[n]代表以n作为结尾的最长连续子数组的乘积 // 递推公式:dp[n] = max(dp[n-1] * val[n], val[n]),即这个有两种可能,一种是以n作为结尾,然后乘上之前的最大值,另一种是不乘之前的值,自己独立成为一个结果 // 我们应该从这两种方案中选择一个较大的值作为结果 // 由于当前值只跟上一个值有关,我们可以使用变量方式来替代递推数组,又因为数组中可能存在负数,有可能导致当前值乘上之前的最大值变成了最小值,因此,我们 // 还需要额外记录一下数组中的最小值 let res = Number.MIN_SAFE_INTEGER; // 由于是乘积关系,因此,最小值和最大值初始化为1 let min = 1; let max = 1; for(let num of nums) { // 由于num是小于0的,因此,如果我们依然乘以原先的最大值,那就可能反而变成最小值,因此当num小于0时,我们交换最大值和最小值,这样,num乘以原先的最小值,就可以得到较大值了 if(num < 0) [min, max] = [max, min]; // 计算最大值和最小值 min = Math.min(min * num, num); max = Math.max(max * num, num); // 最终结果在上一个结果和max间取最大值 res = Math.max(res, max); } return res; };
复制代码2.5 LeetCode 322. 零钱兑换

2.5.1 解题思路
1. 递推状态: 我们使用多少个硬币,取决于要凑的金额的面额有多大,因此,我们的递推状态为: dp[n]
2. 递推公式: 假如我们要凑的面额是 n ,那么我们能凑够的最小的硬币数量应该是 n-coin 面额硬币数量再加上当前这枚硬币 coin 的数量1,并且每次都取最少的数量即可。因此,我们最终的递推公式应该是: dp[n] = min(dp[i-coin] + 1), 即面额为 n 的钱需要我们在所有的拼凑方案中,取一个最小值,而每一个拼凑方案应该是当前面额i减去当前使用的硬币面额 coin 再加上当前硬币的数量 1 。
3. 边界条件: 当面额为0时,我们需要0枚硬币。
4. 程序实现: 我们再拼凑面额的时候,有一些特殊情况需要考虑,如:
如果当前要拼凑的面额比硬币的面额要小,那么我们无法使用当前硬币拼凑成目标面额
如果 i-coin 面额都无法拼凑成功的话,那么我们肯定也无法使用 coin 面额的硬币拼凑出目标面额,因为 i-coin 是前置条件。
2.5.2 代码演示
function coinChange(coins: number[], amount: number): number { // 我们需要计算出每一个面额所需要的硬币数量 let dp: number[] = new Array(amount+1); // 初始时全部填充为-1代表不可达 dp.fill(-1); // 拼凑0元需要0枚硬币 dp[0] = 0; // 循环每一个面额 for(let i=1;i<=amount;i++) { for(let coin of coins) { // 如果当前要拼凑的面额比当前硬币还小,那就不能使用当前硬币 if(i < coin) continue; // 如果没办法拼凑到dp[i-coin]的硬币,那么自然也不可能使用coin面额的硬币拼凑到dp[i] if(dp[i - coin] === -1) continue; // 如果当前的匹配方案没有使用过,或者使用当前匹配方案的结果比上一个匹配方案的结果大,说明我们找到了更小的拼凑方案,那么我们就把当前拼凑方案替换之前的拼凑方案 if(dp[i] === -1 || dp[i] > dp[i - coin] + 1) dp[i] = dp[i - coin]+1; } } return dp[amount]; };
复制代码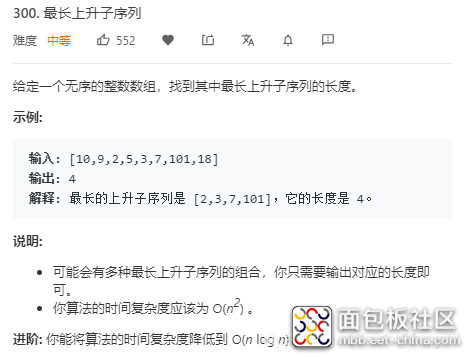
2.6.1 解题思路
>>概念扫盲:
a. 递增子序列:
你可以在一个完整的序列中,“跳着”选择元素,并且下一个元素必须不能小于上一个元素。所谓“跳着”,就是指元素索引不需要连续,如下面示例:
# 原始序列1, 4, 2, 2, 3, 5, 0, 6 # 递增子序列 1, 2, 2, 3, 5, 6
复制代码严格递增子序列是在递增子序列的基础上多了一个限定条件,就是下一个元素不能等于上一个元素,只能大于,如下示例:
# 原始序列1, 4, 2, 2, 3, 5, 0, 6 # 严格递增子序列 1, 2, 3, 5, 6
复制代码2. 递推公式: 我们要算出以第n个元素作为结尾的最长递增子序列的长度,就要找出他上一个合法的最长递增子序列的最后一个元素j,而我们第n个元素作为结尾的最长递增子序列长度就是上一个最长递增子序列长度加一,我们只需要将所有满足这个条件的最长递增子序列长度的最大值求出来就是最终的结果,即: dp[n] = max(dp[j] + 1) | j<n & val(j) < val(n)
3. 边界条件: n为1时,最长递增子序列长度为1
4. 程序实现: 由于我们的递归状态定义的是以n作为结尾的最长递增子序列的长度,因此,我们每一项的初始值默认都是1,至少要选择当前的数。
2.6.2 代码演示
function lengthOfLIS(nums: number[]): number { const dp: number[] = []; let res: number = Number.MIN_SAFE_INTEGER; for(let i=0;i<nums.length;i++) { // 每一项都初始化为1,因为dp[i]代表以i位置作为结尾的最长递增子序列的长度,那我们最少都应该选择i这个数,长度就是1 dp[i] = 1; // 在i位置之前找到满足nums[j] < num[i]的值 for(let j = 0; j < i;j++) { if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1); } // 到此,我们已经找到了一组最长递增子序列了,更新一下res res = Math.max(res, dp[i]); } return res; };
复制代码今天的刷题到此暂告一段落。
从上面刷的几道题其实我们不难发现,无论是递推算法还是动态规划,都有一定的套路可循,虽然这个套路学起来也并不简单,但是至少有了明确的学习方向,我们可以通过:递推状态定义、递推公式(状态转移方程)推导、边界条件确立、程序实现这四个通用套路将一个看似复杂的递推或动规程序逐一分析解决。
当然,上面的程序实现,为了更容易理解,没有使用太多的技巧进行优化,并不一定是最优的,未来如果有机会,将和大家分享动态规划的优化技巧。也欢迎大家与我们多多交流~






 /1
/1 

