PWM是一种周期固定,而高低电平占空比可调的方波信号。
PWM通过简单的RC滤波网络可以得到与信号占空比成线性关系的直接电压,从而实现D/A转换。如下图所示:
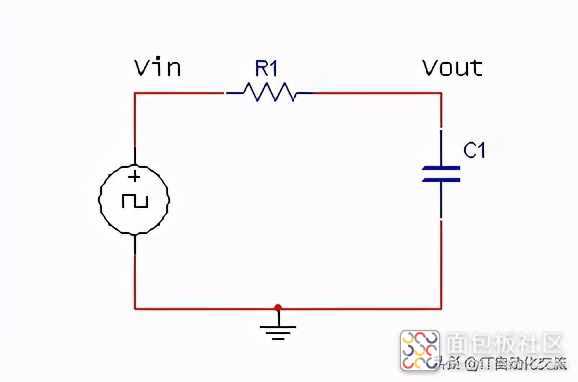
PWM滤波电路
滤波电路中的R,C参数与PWM的周期以及直流电压的精度要求直接相关,必须从理论上详细分析。
假设PWM波的频率为f,高电平电压为V,占空比为a。
如果RC网络的时间常数远大于PWM波的周期T,Vin和Vout波形如下图所示:
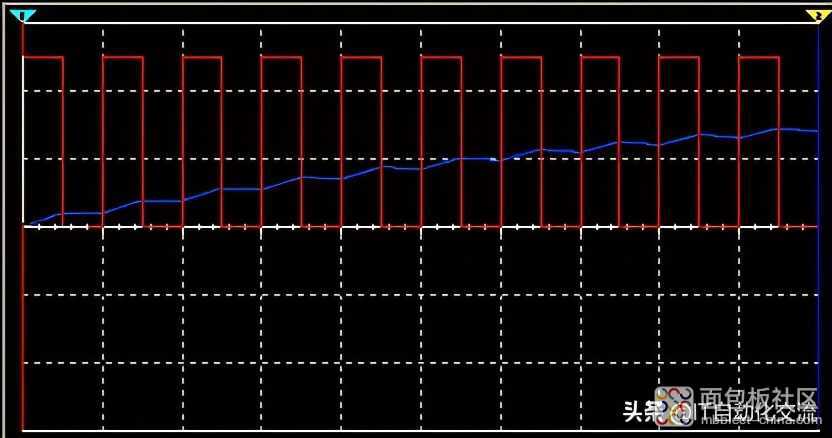
PWM滤波之后的波形
处于瞬态时,Vin在高电平持续时间内向电容充电,电容积累电荷,在低电平持续电间内电容向Vin放电,电容释放电荷。
电容积累的电荷数多于释放的电荷数。
因此电容电容两端的直波电压不断爬升,最终达到稳态。
处于稳态时,电容积累的电荷与释放的电荷数量相等,因此电压会在一个稳定的电压值附近做小幅度的波动,忽略这样的纹波,则电容两端的电压与PWM占空比呈线性关系。
如下图:
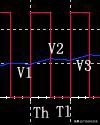
充放电波形
当t<Th时,电容充电,电容两端电压表示为:
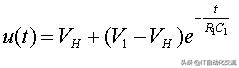
充电方程
由于T=(Th+Tl)<<R1C1,所以t/(R1C1)<<1,利用级数展开,得到:
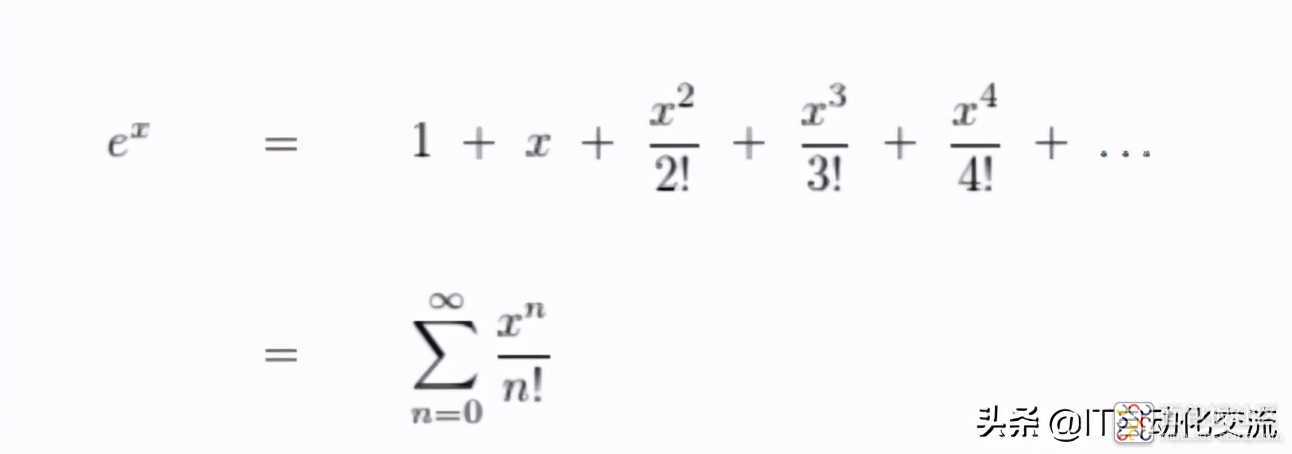
e指数函数的泰勒级数展开
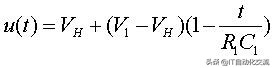
级数展开近似
当t=Th时,
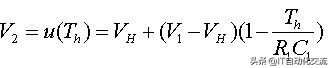
t=Th时的电压
当t>Th且t<Th+Tl时,
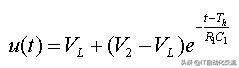
电容放电方程
当t=Th+Tl时,
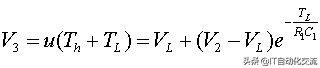
t=Th+Tl时的电压
在这样的稳态下,电容在一个周期内的充放电会相等,所以有V1=V3,即
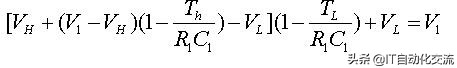
充放电电压相等
忽略二阶小量,得到,
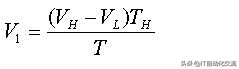
忽略二阶小量的数值
由于PWM的占空比定义为:
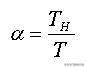
占空比定义
由于V1=V3≈V2,所以当电路处于稳态时,电容两端的电压近似为直流电压,表示为:
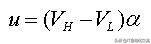
输出电压与占空比、高低电平的关系
可见,电容两端的电压与PWM高低电平之差以及占空比成比例关系。
数字处理器通过调整PWM信号的占空比就可以调节通过R、C滤波电路得到的直流电压的幅度。
直流电压精度定义为:
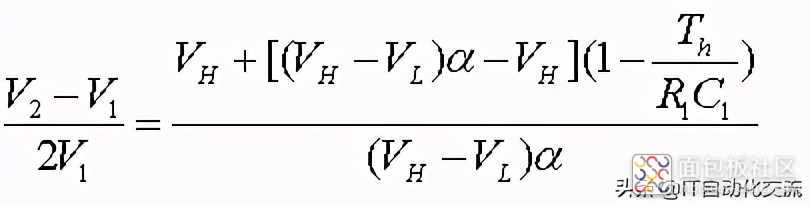
精度计算
设计PWM波RC滤波电路时,应根据响应时间要求,确定时间常数,并且使RC时间常数远大于PWM周期。
RC充放电时间常数应尽量相等。此外还应根据电压精度要求确定RC参数。
在整个推导计算过程中,我们在电路的充放电方程中忽略了二阶小量,为了达到精度要求,二阶项至少比一阶项相差1个数量级,即10倍。
充放电方程级数展开的一阶项为t/(R1/C1),二阶项为t*t/(R1*R1*C1*C1)/2。
二阶项与一阶项的比值为t/R1/C1/2,
在信号的一个周期内,t最大为信号的周期,而R1*C1为R、C滤波网络的时间常数。
由该公式可知,为了保证精度要求,该时间常数至少为信号周期的5倍。
比如,当PWM信号的频率为100KHz时,R、C滤波网络的时间常数至少为50us。
可以选择10KΩ的电阻,以及103(10nF)的电容;
来源:物联网全栈开发








 /5
/5 


