在数字、模拟电路中,我们经常遇到带宽(BW)和采样频率(Fs)这两个参数,如何理解呢?我们通过下面一个应用实例来解释说明一下。
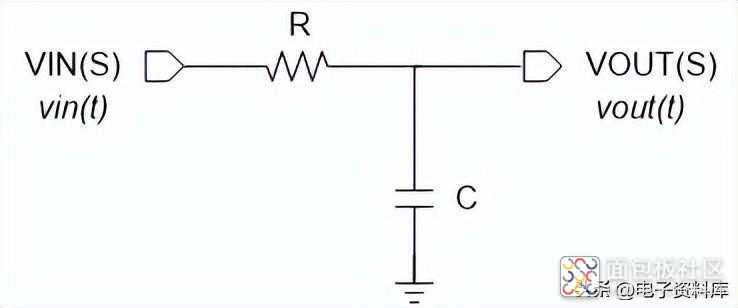
以电阻R和电容C构成的低通滤波器系统为例,如图(一)所示,根据自控原理的理论基础可知,其传递函数定义为:
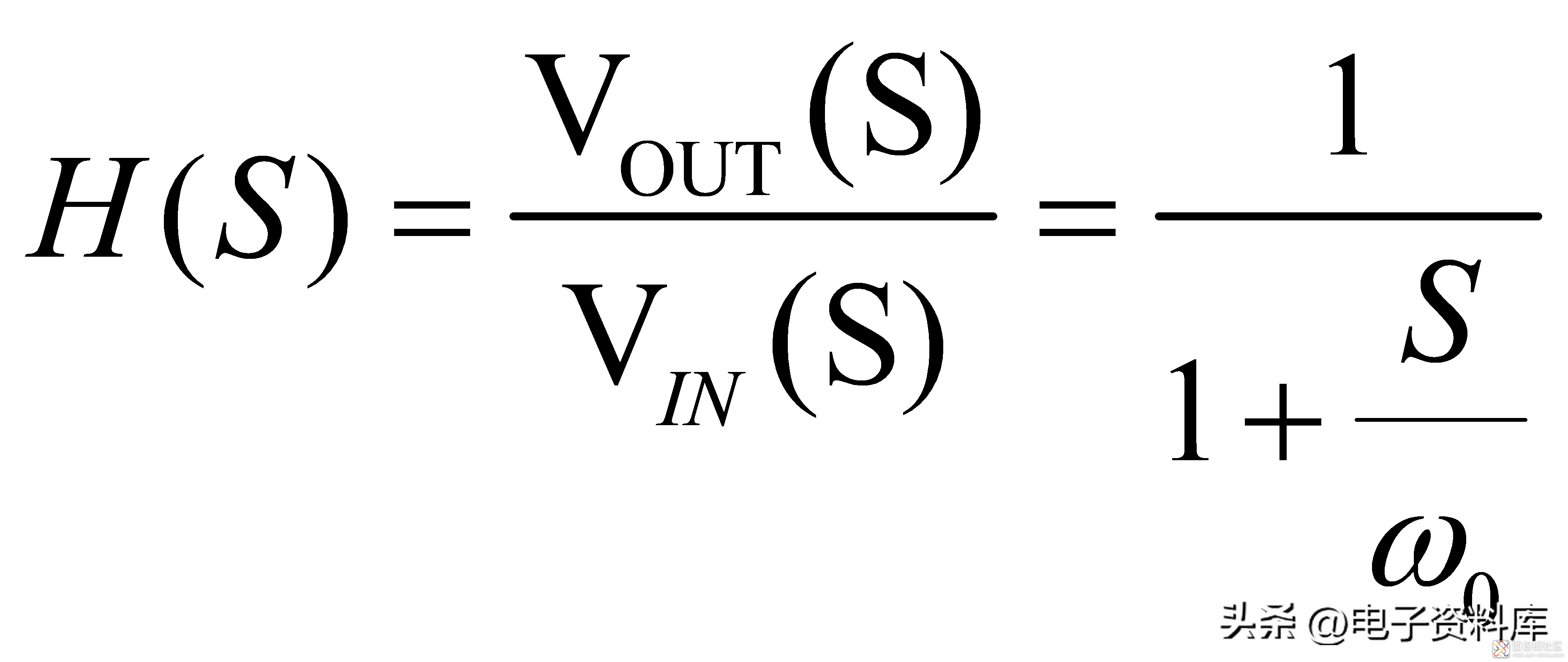
(1)
其中,
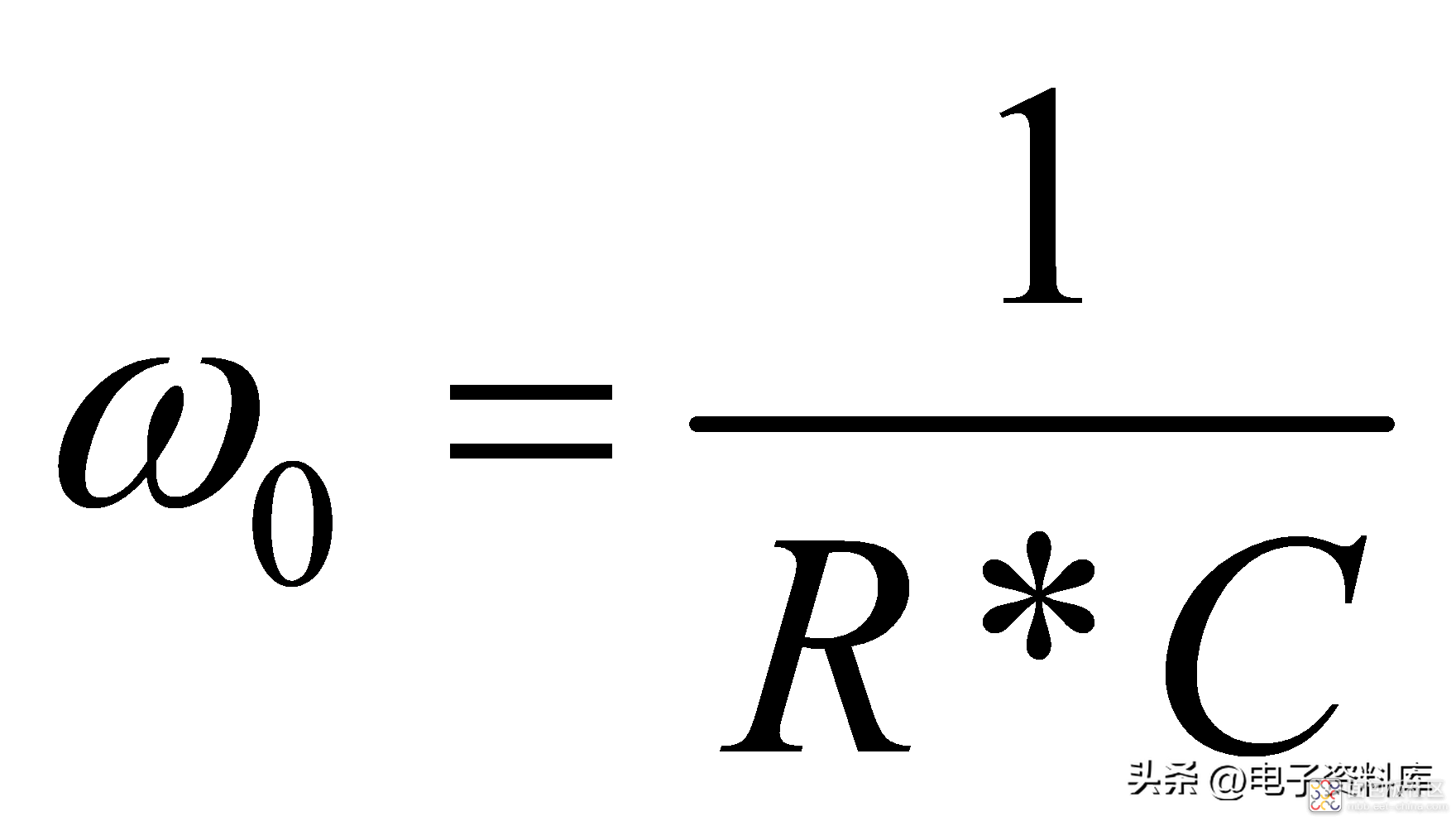
,为角频率(单位是弧度/秒)。角频率和通常意义的频率

(单位为Hz)之间的关系是:
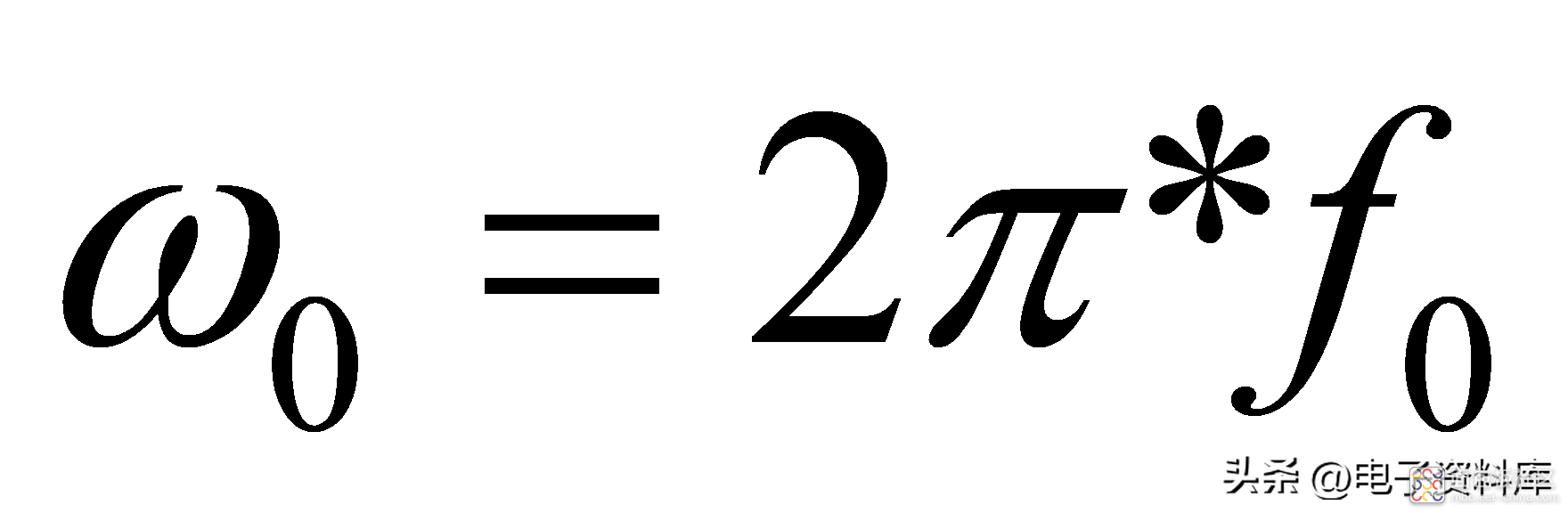
。
一阶低通滤波器的幅频特性Magnitude和相频特性Phase分别为:
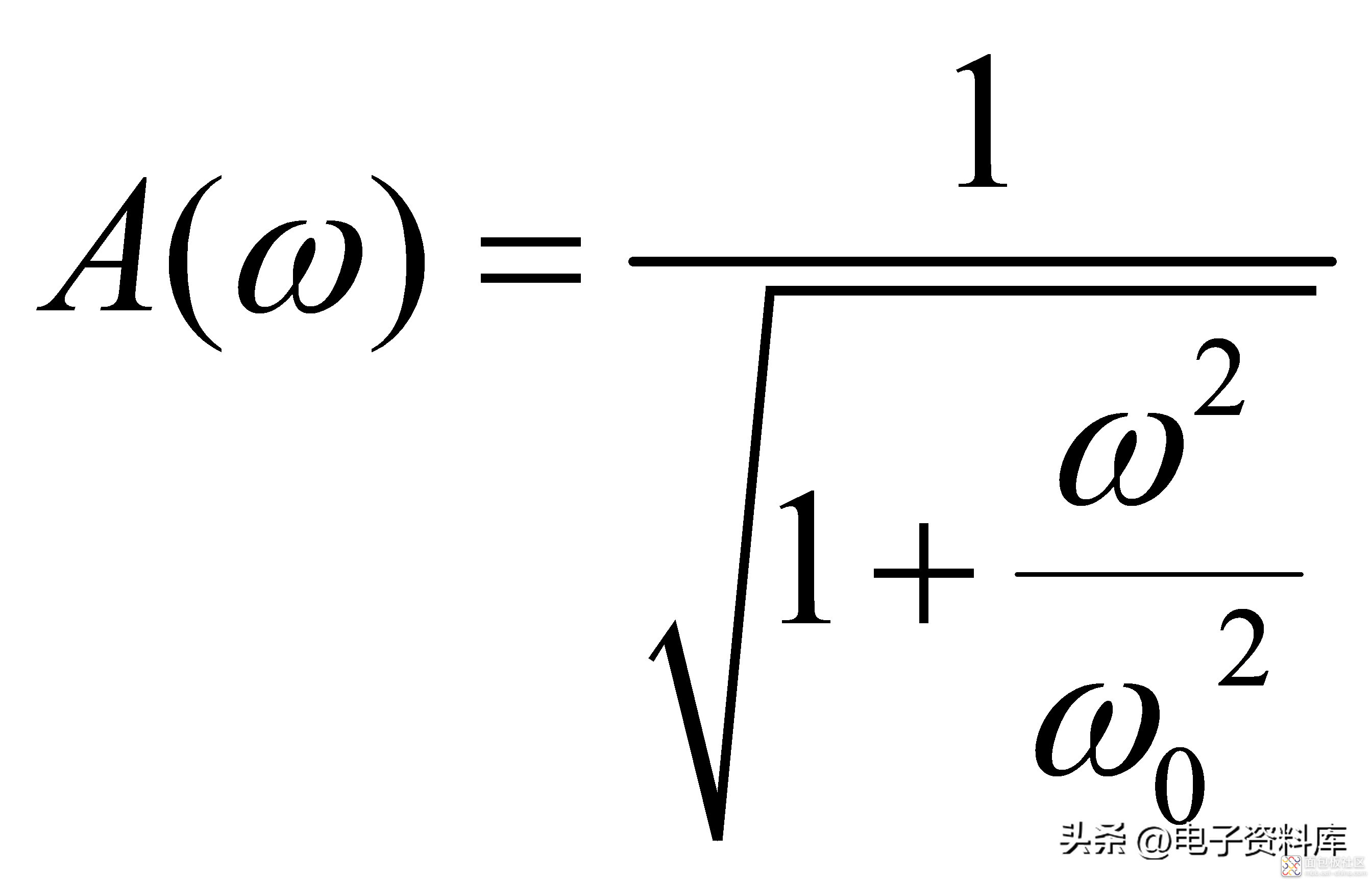
(2)
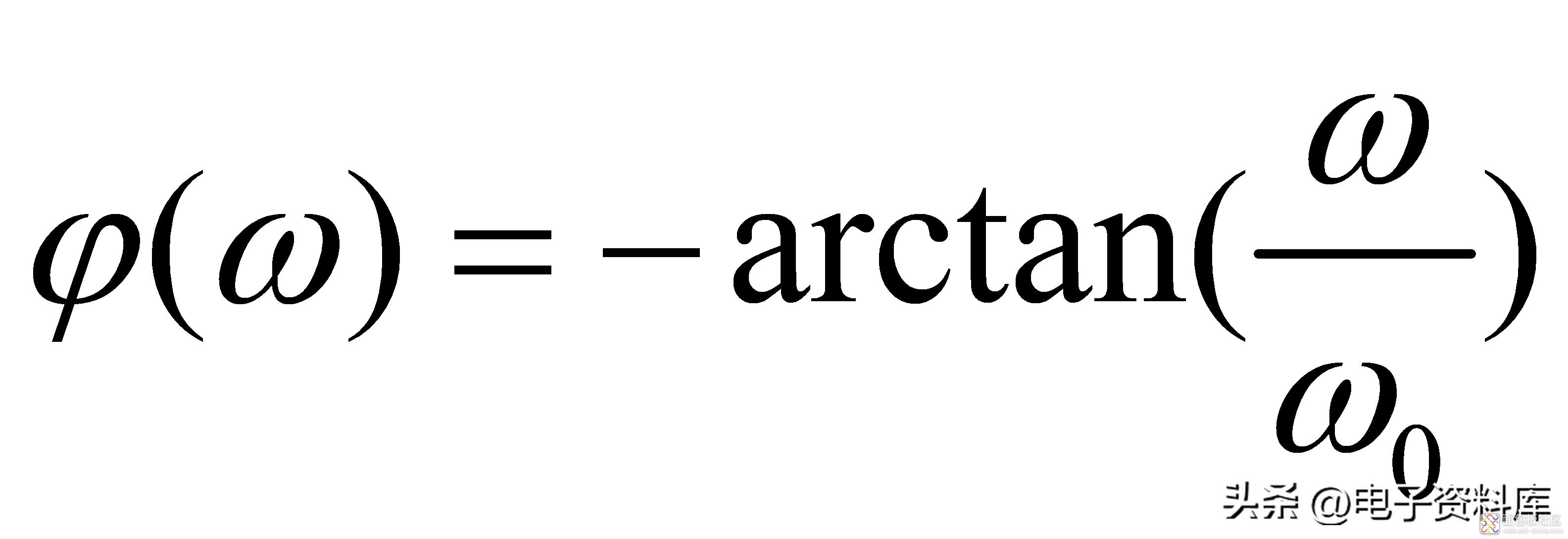
由公式(2)和(3)不难得出如下结论:
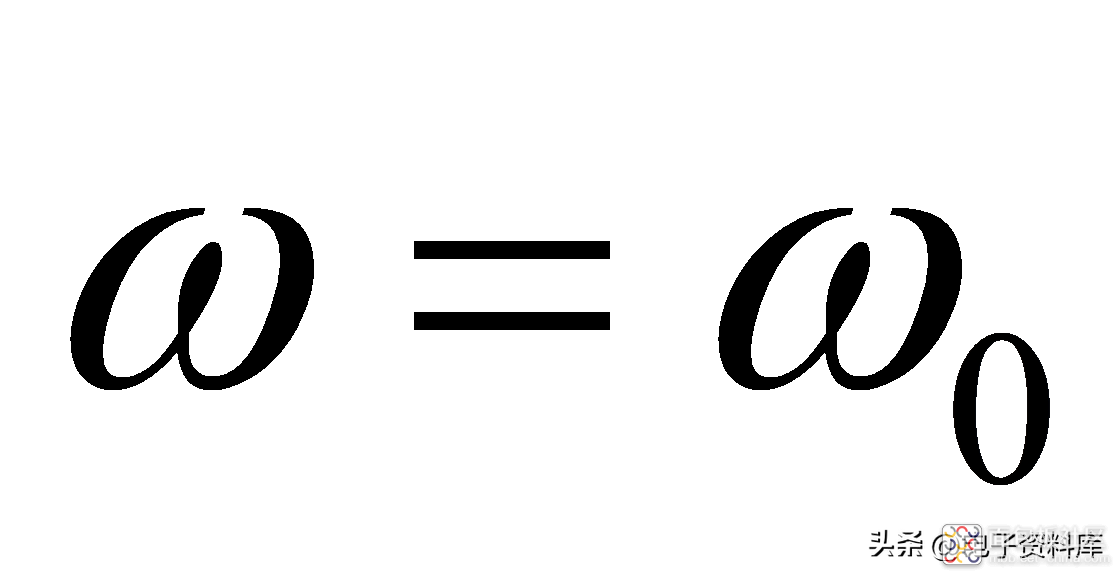
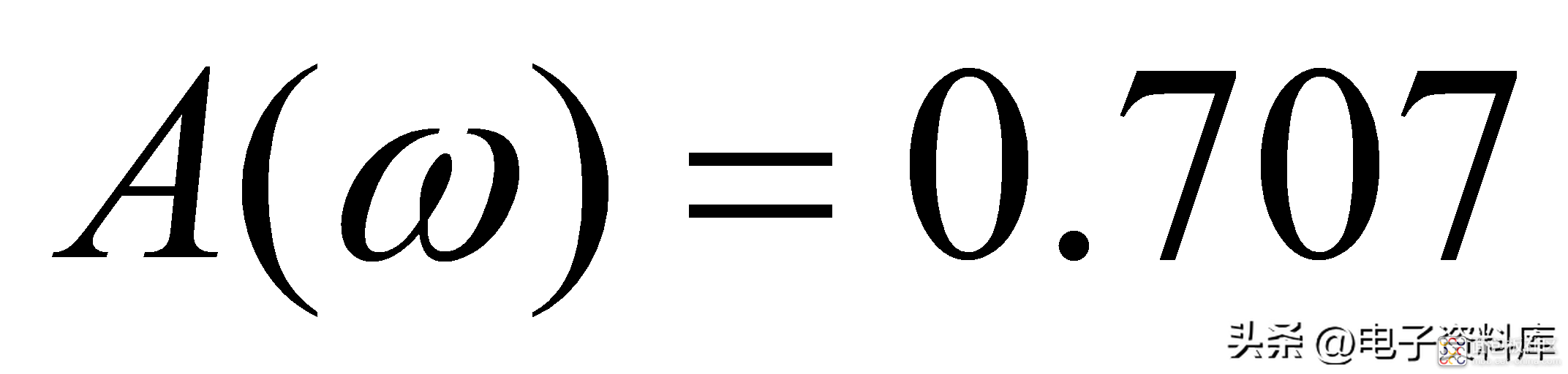
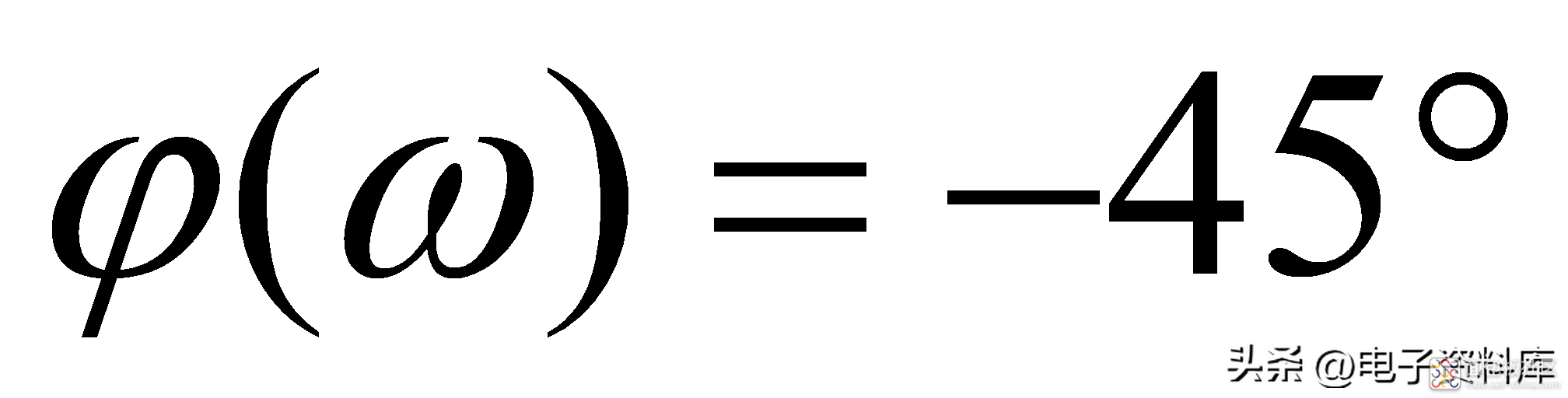
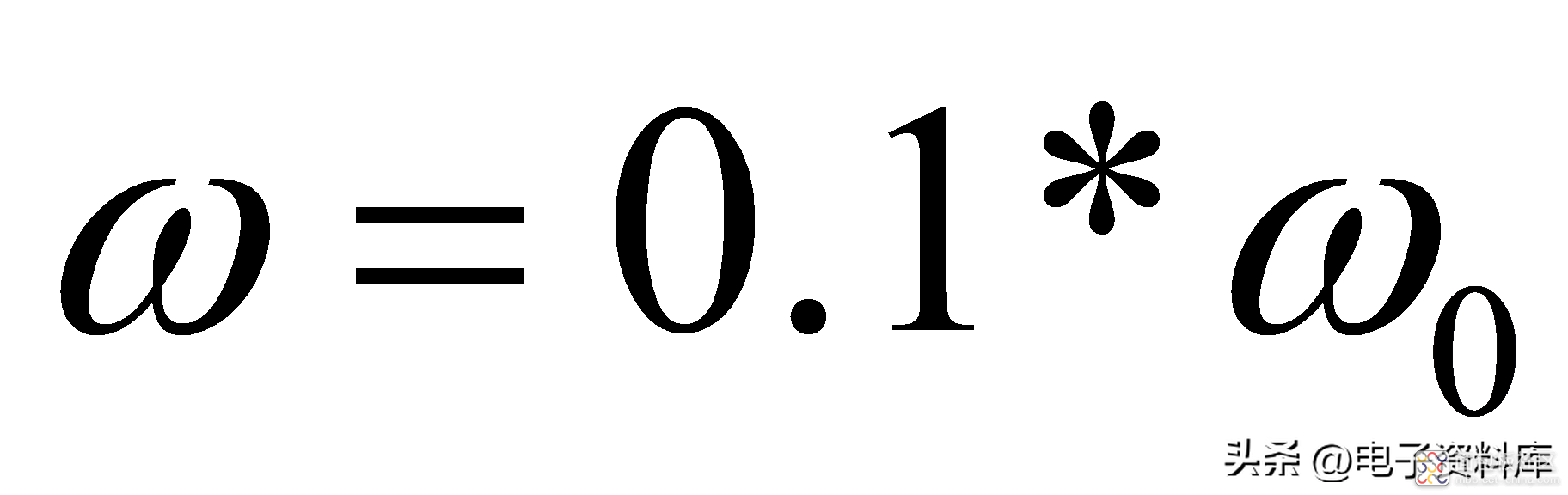
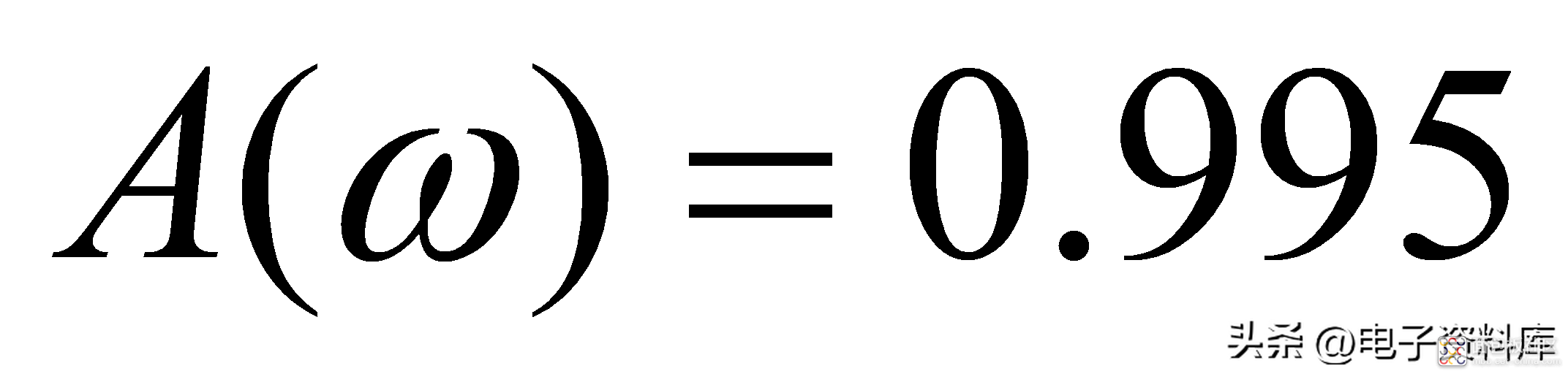
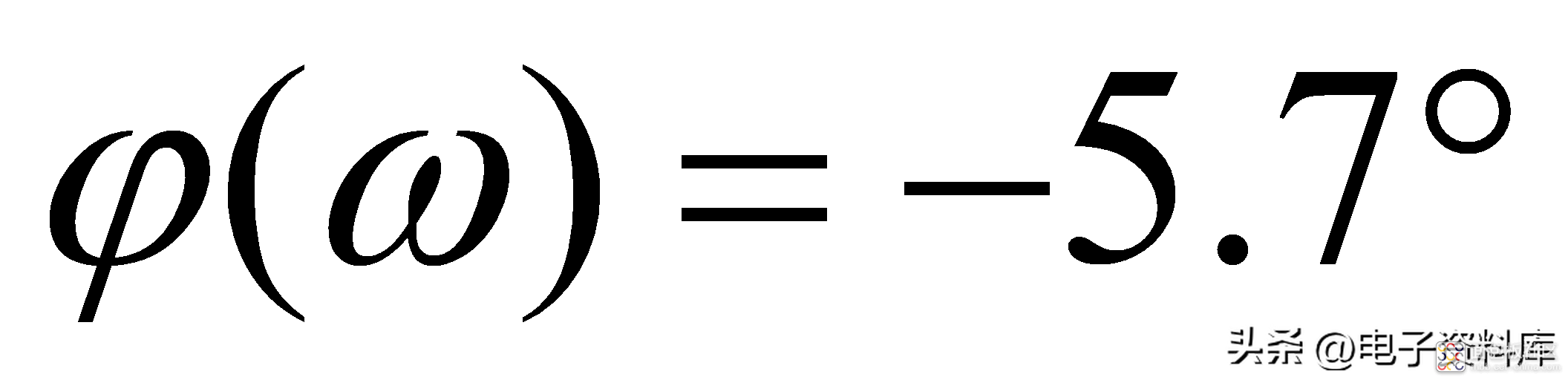
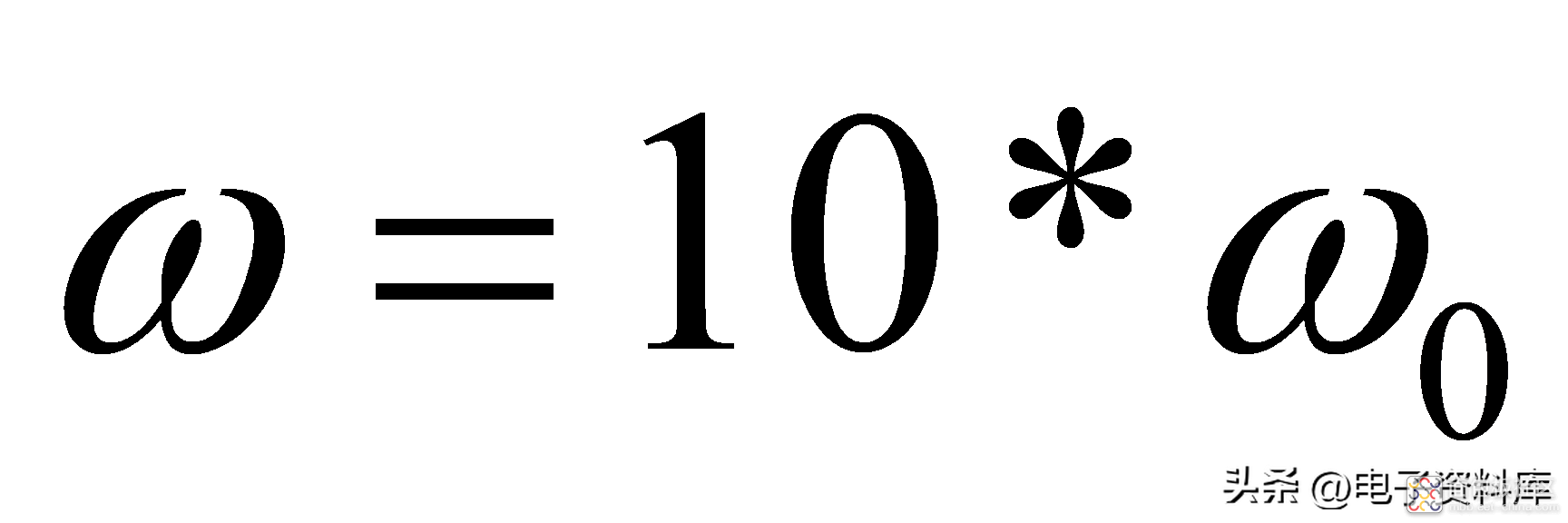
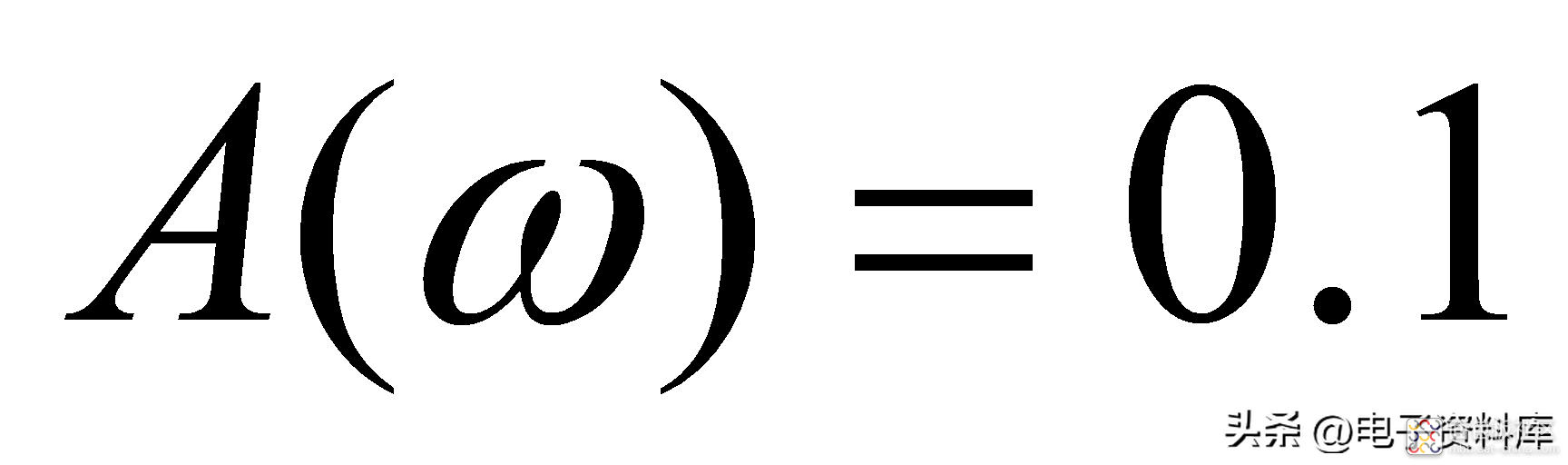
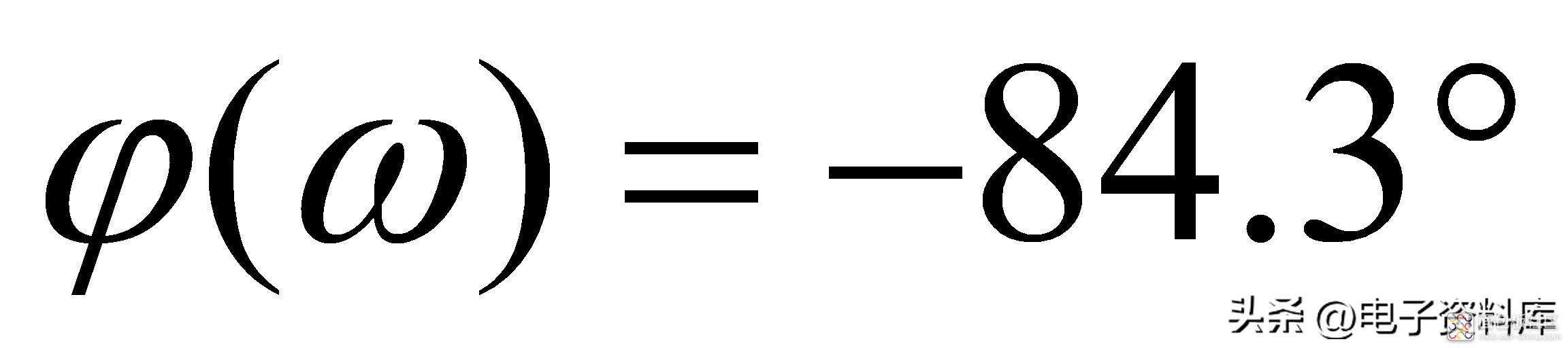
习惯上,将-3dB信号幅度衰减所对应的频率,定义为系统的带宽;以图(一)所示一阶低通滤波器为例,其带宽为
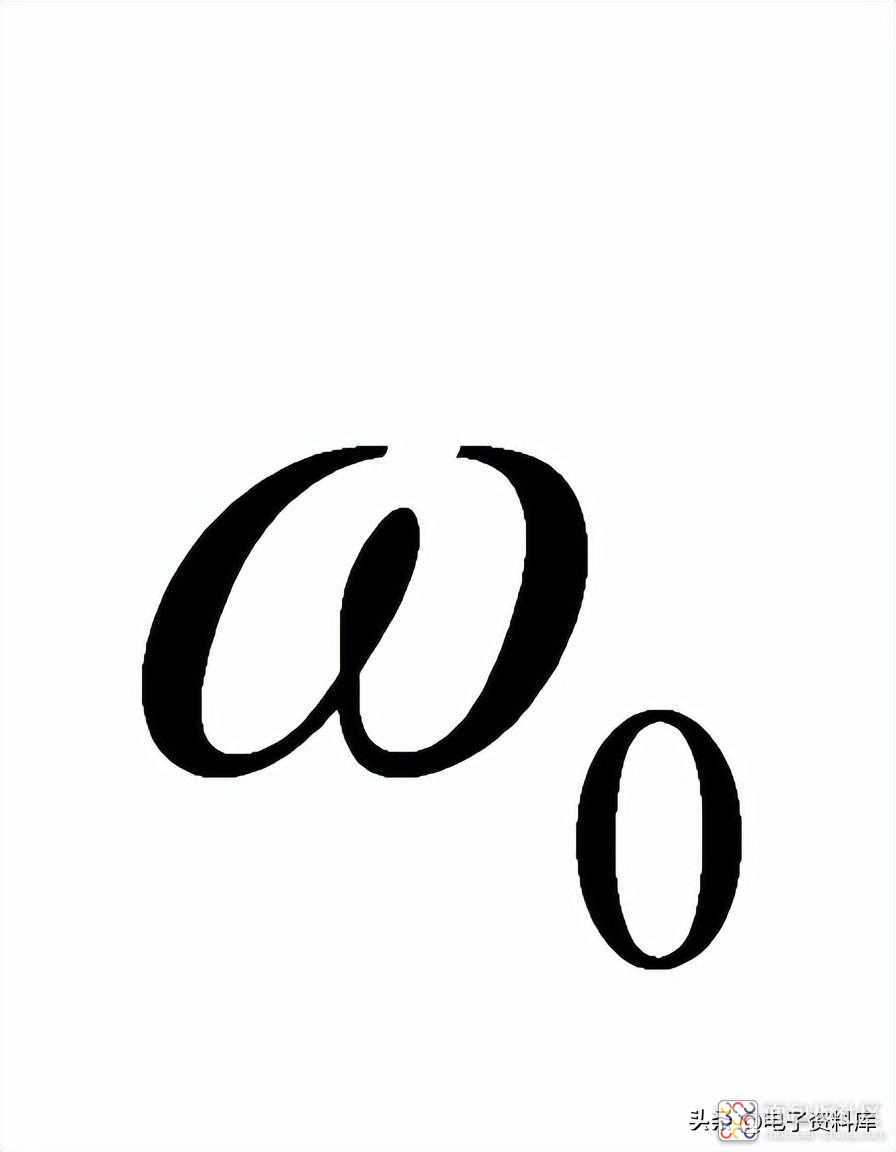
。
这里还是以一阶低通滤波器为模型进行说明(计算过程有兴趣请参考自控原理等相关书籍),当输入信号为:
即:
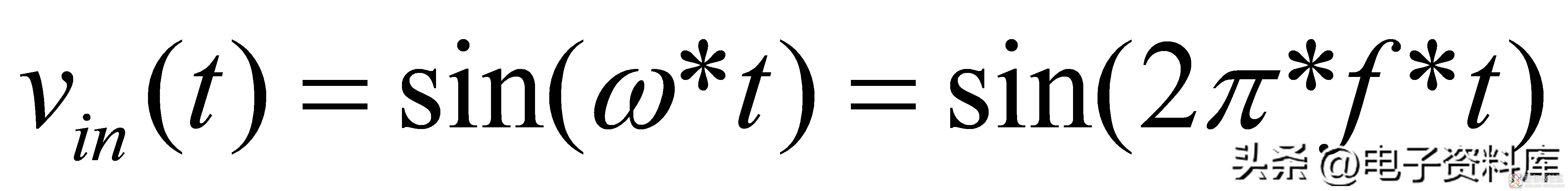
(4)
则:
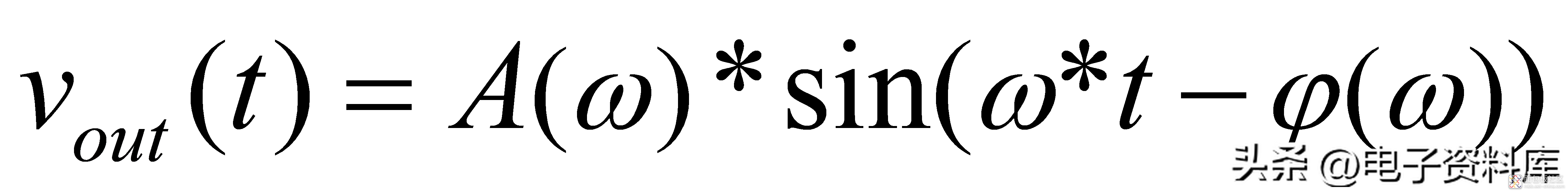
(5)
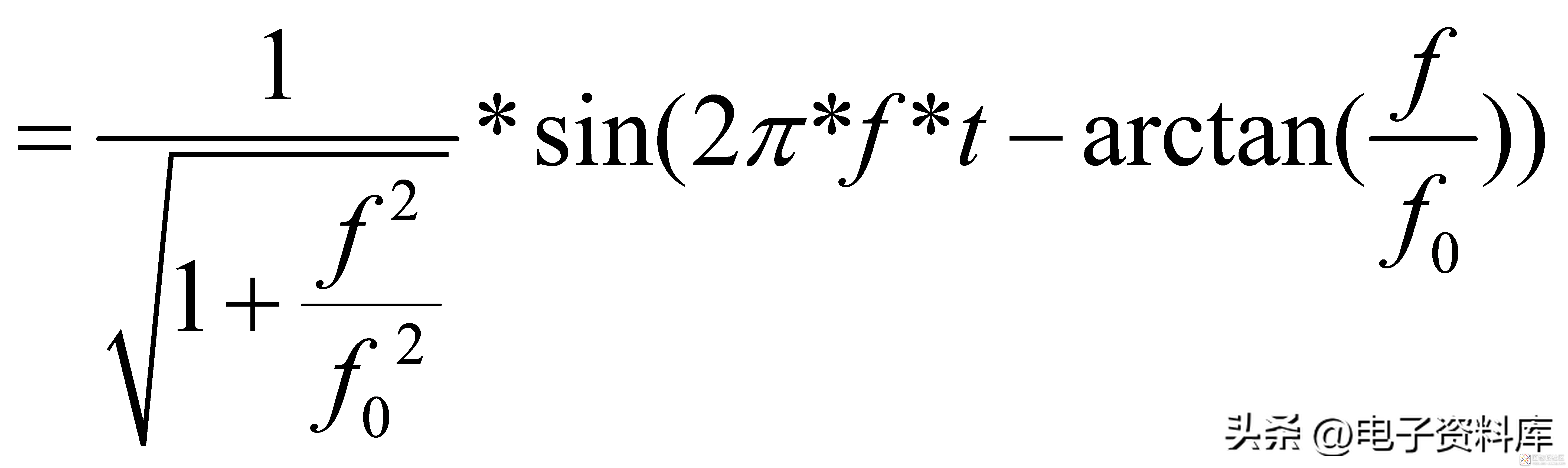
为了方便起见,将一阶低通滤波器的带宽归一化,即令
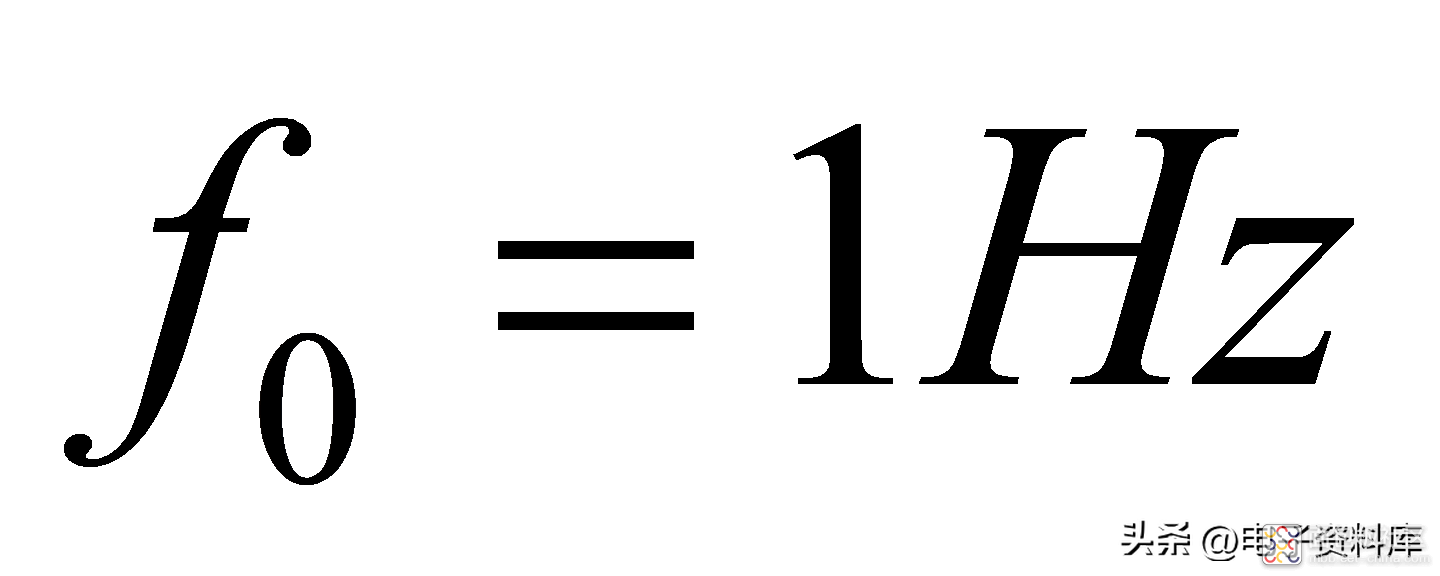
,对于相同幅度不同频率的输入信号,其输入/输出关系如图(二)所示,可以看到:随着正弦输入信号的频率越来越高,一阶低通滤波器输出的幅值越来越小,相移越来越大。
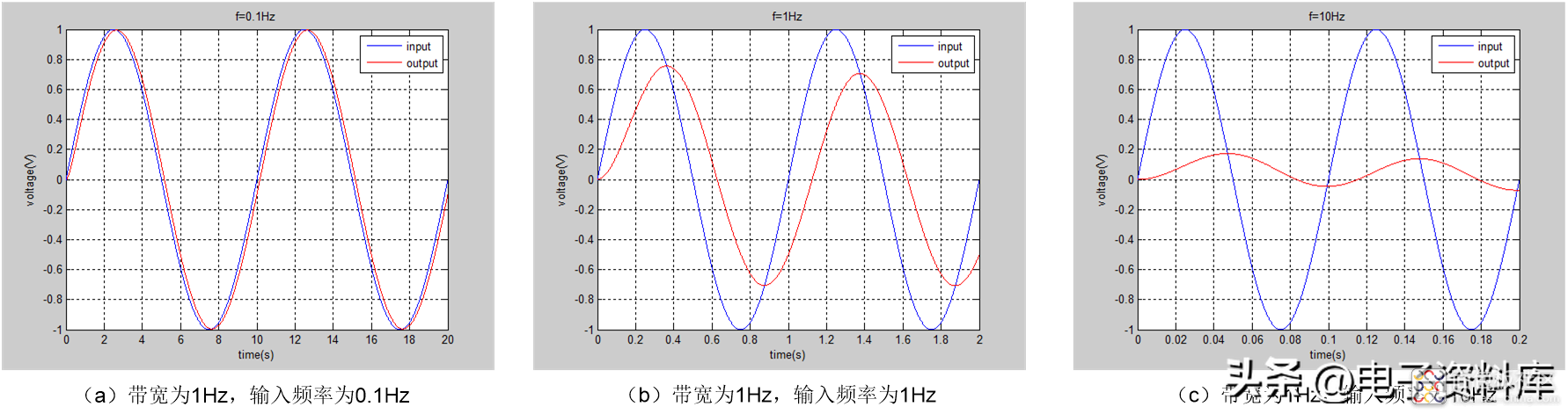
图(二) 一阶低通滤波器对不同频率正弦输入信号的响应
即
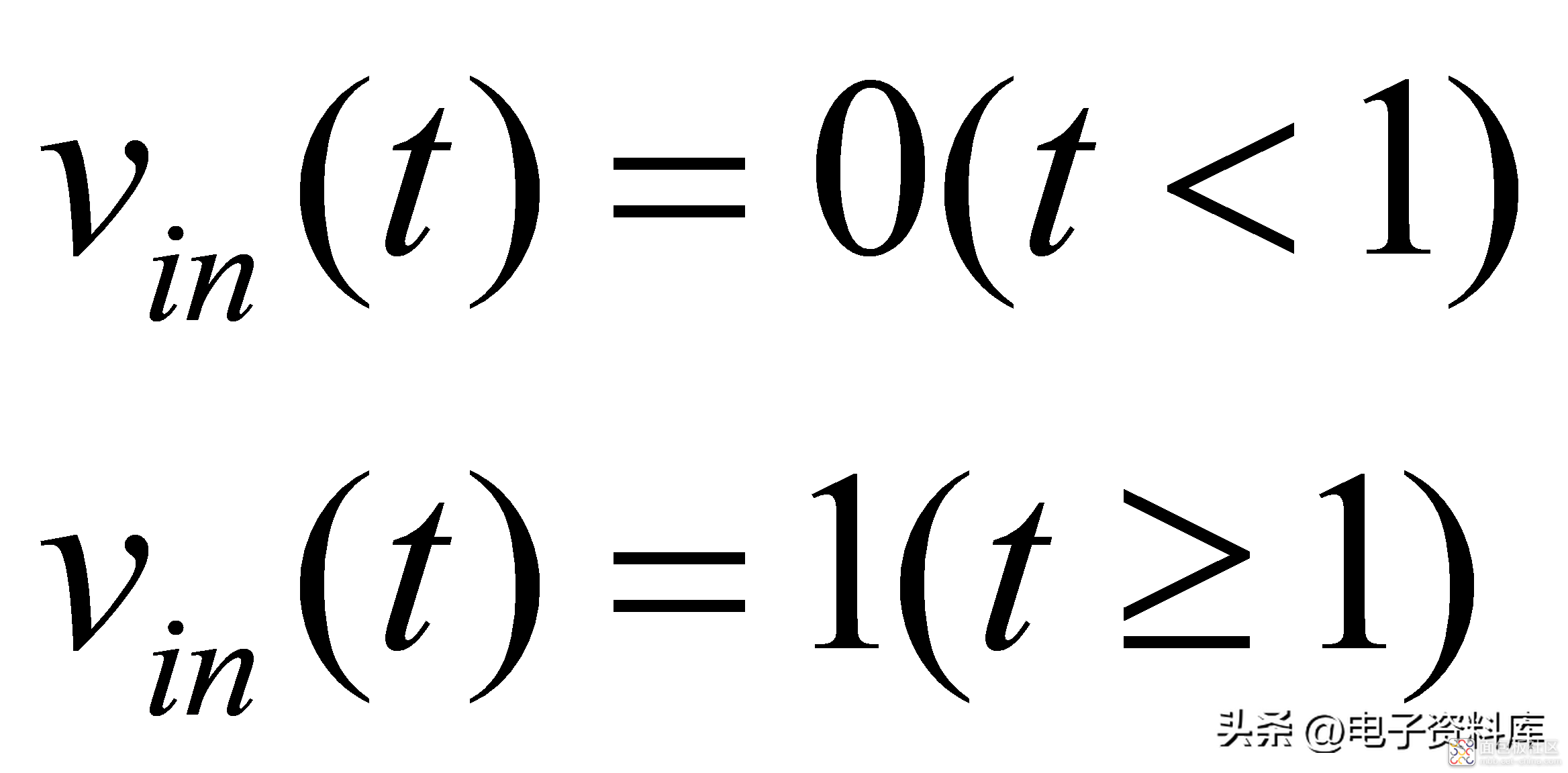
(6)
则
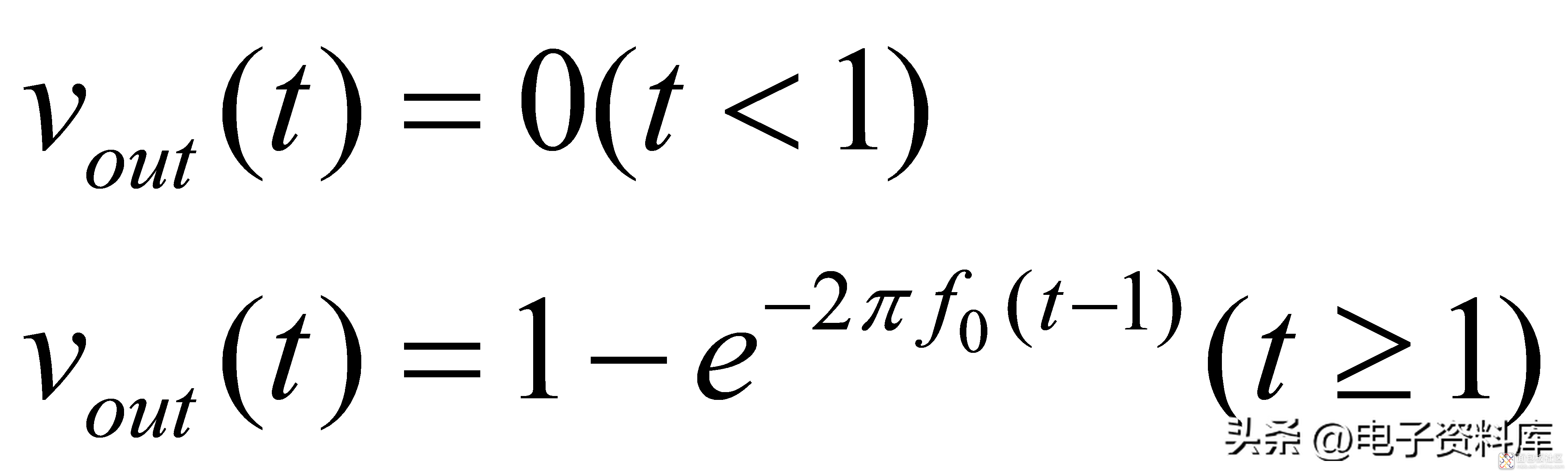
(7)
从公式(7)可以看出,
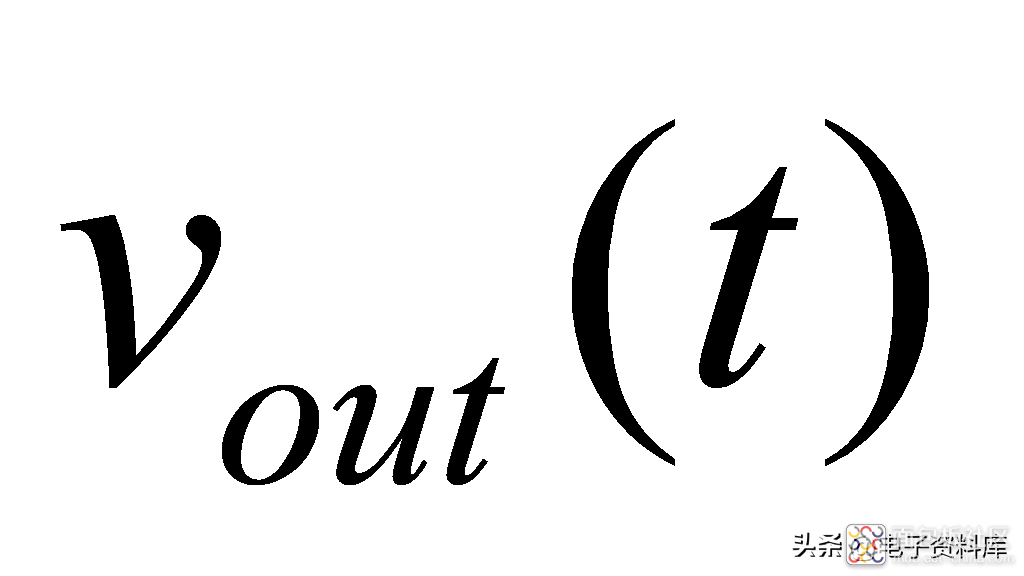
settle到90%的幅值所需的时间是:
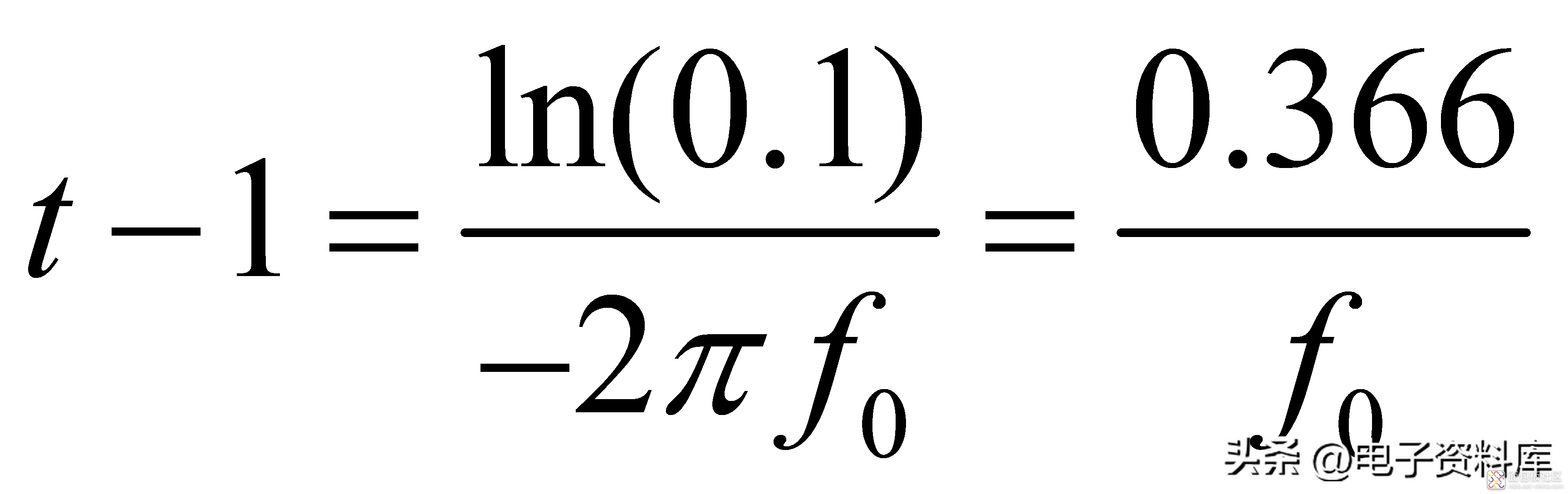
(8)
因此一阶低通滤波器的带宽
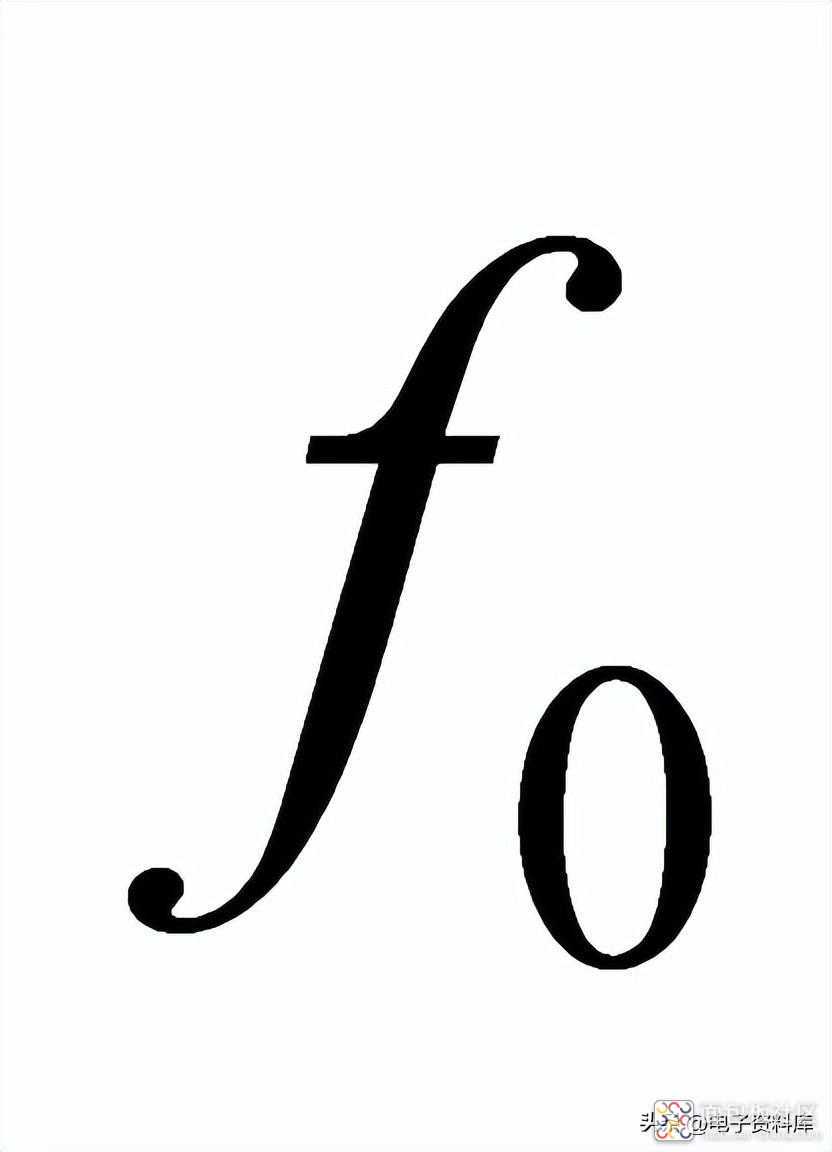
越大,则系统对输入信号的响应越快,其输入/输出关系如图(三)所示,
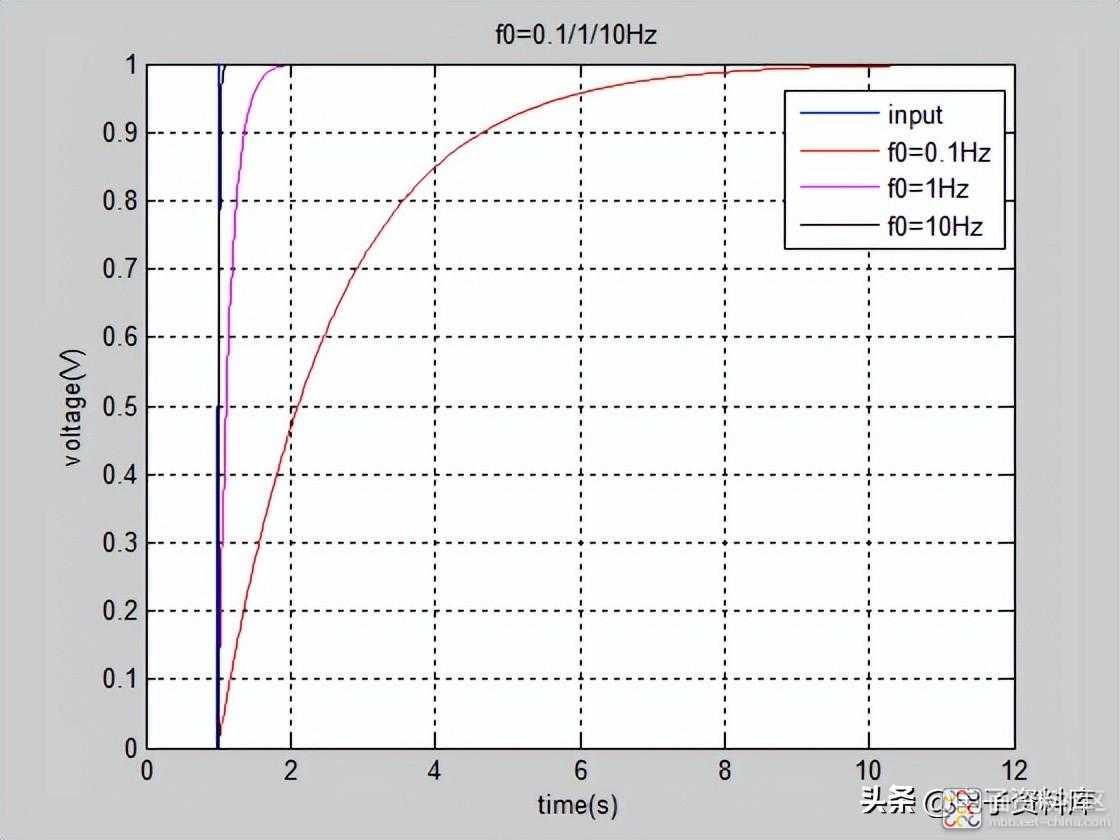
以上分析均基于一阶低通滤波器模型,对于高阶滤波器模型的带宽及其响应,有兴趣的读者可以参考自控原理相关教材,这里不做赘述。
MagnTek公司MT910x系列线性霍尔产品,可以用一阶低通滤波器模型来近似,如图(四)所示为典型应用框图:MT910x检测外界磁场信号
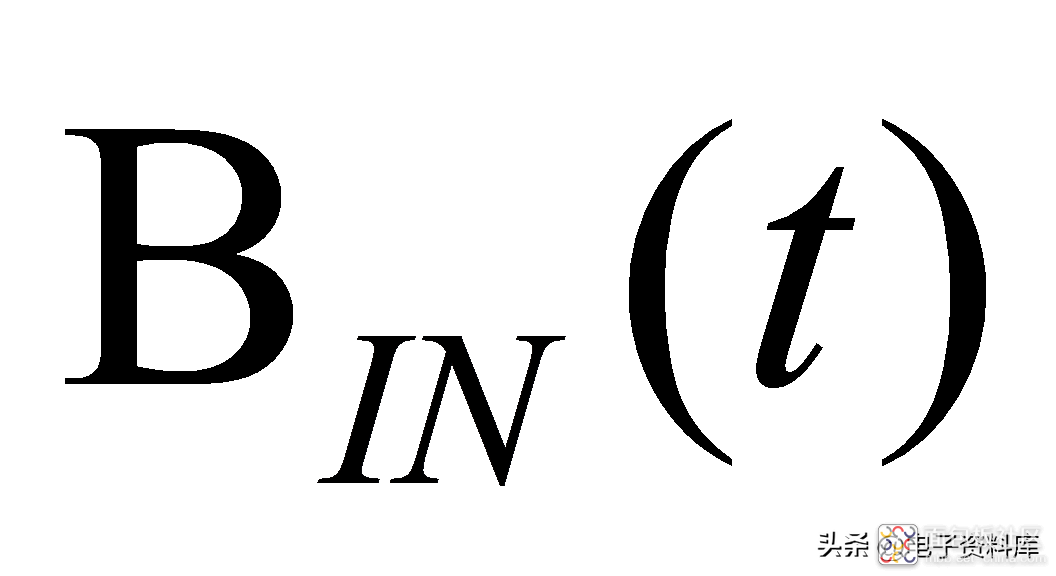
,并将其转化为电压信号
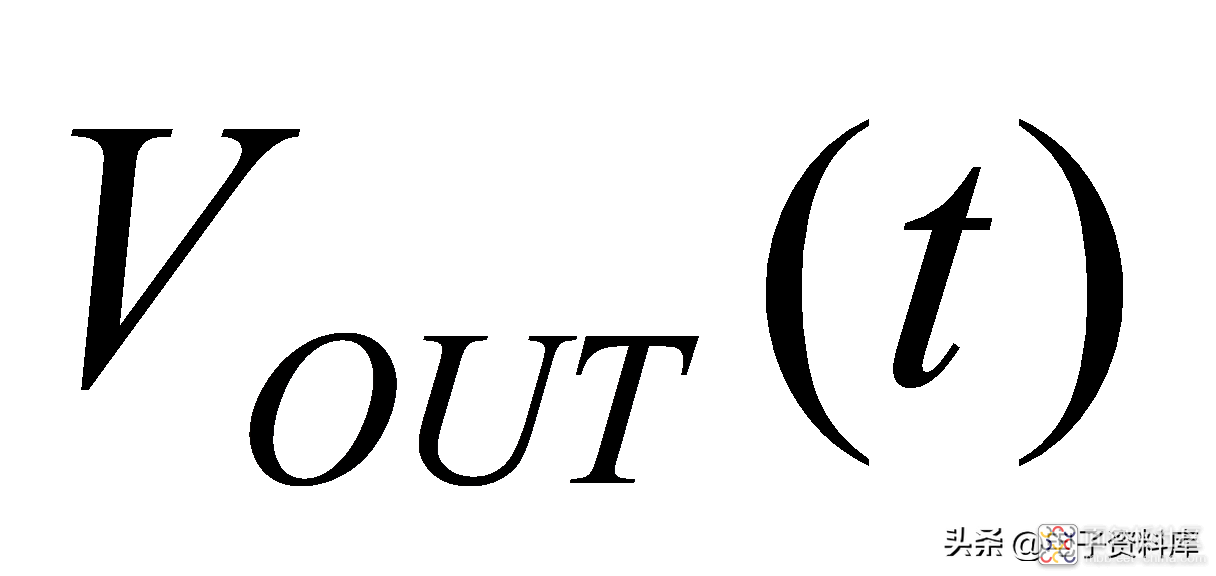
,客户可以用ADC对输出电压信号
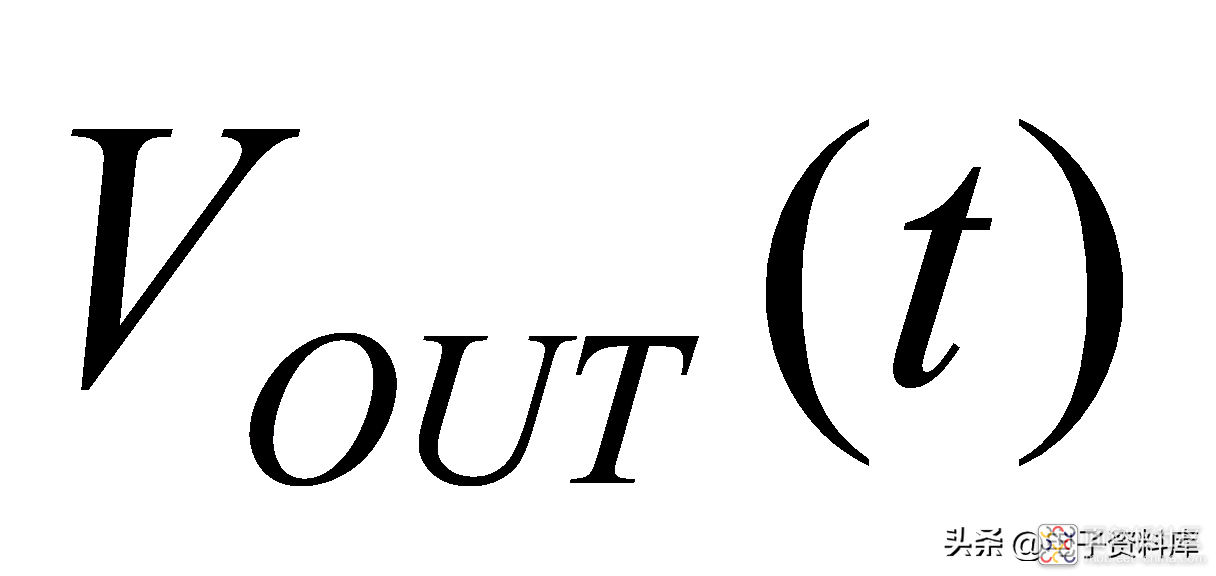
进行采样并将其转化为数字信号
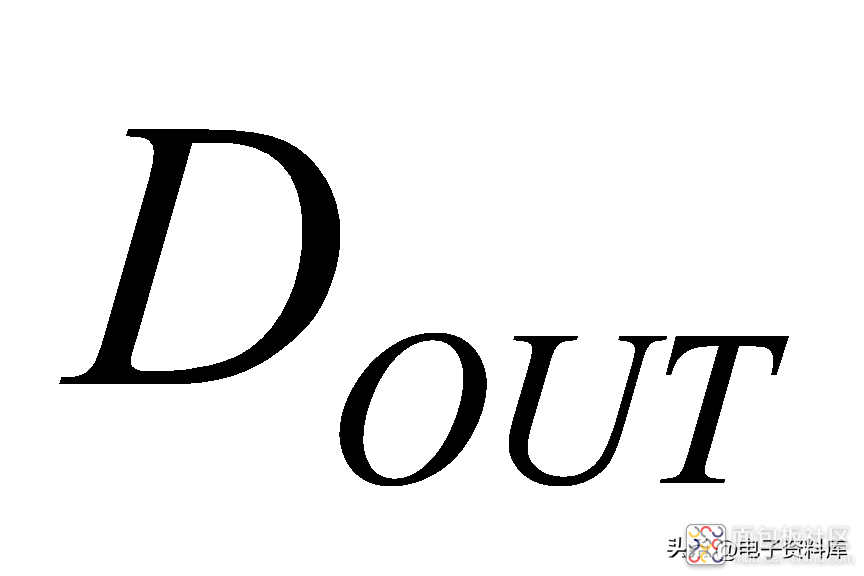
,以便后续进行更为复杂的数字信号处理。
这里,从
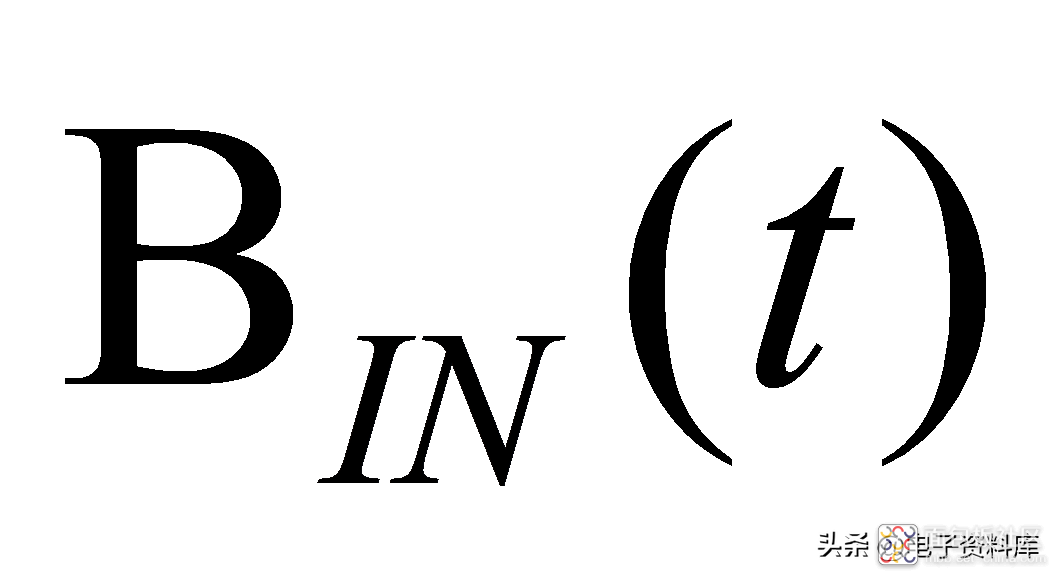
到
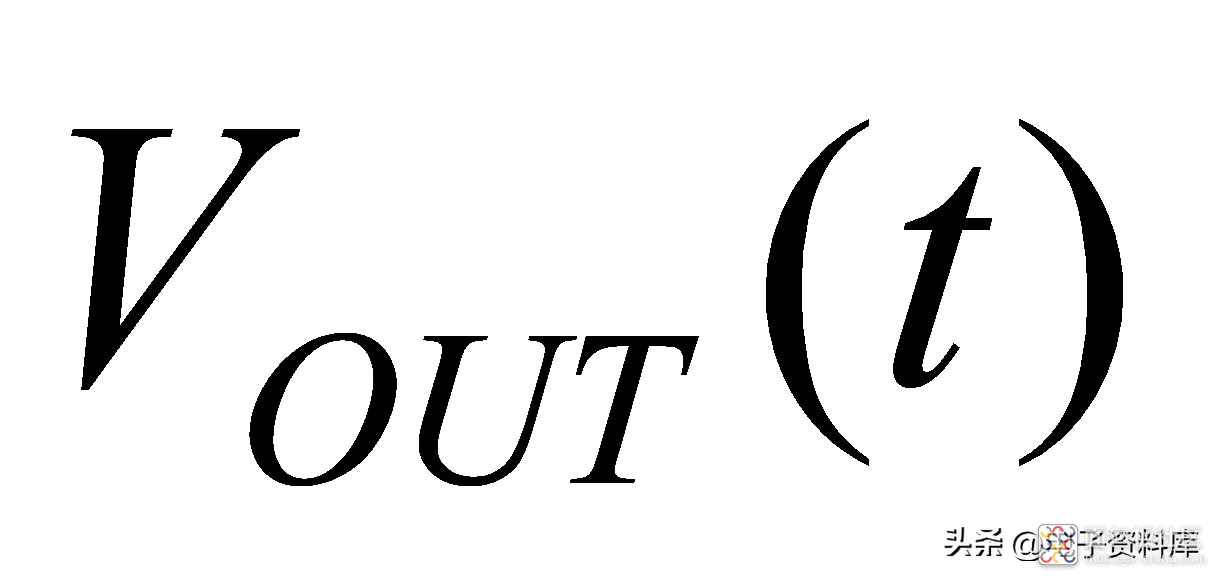
之间便可以用一个带宽为30KHz的一阶低通滤波器模型来近似(需要在公式(1)的分母上乘以MT910x的灵敏度)。有兴趣的读者可以推导下针对不同外界输入磁场
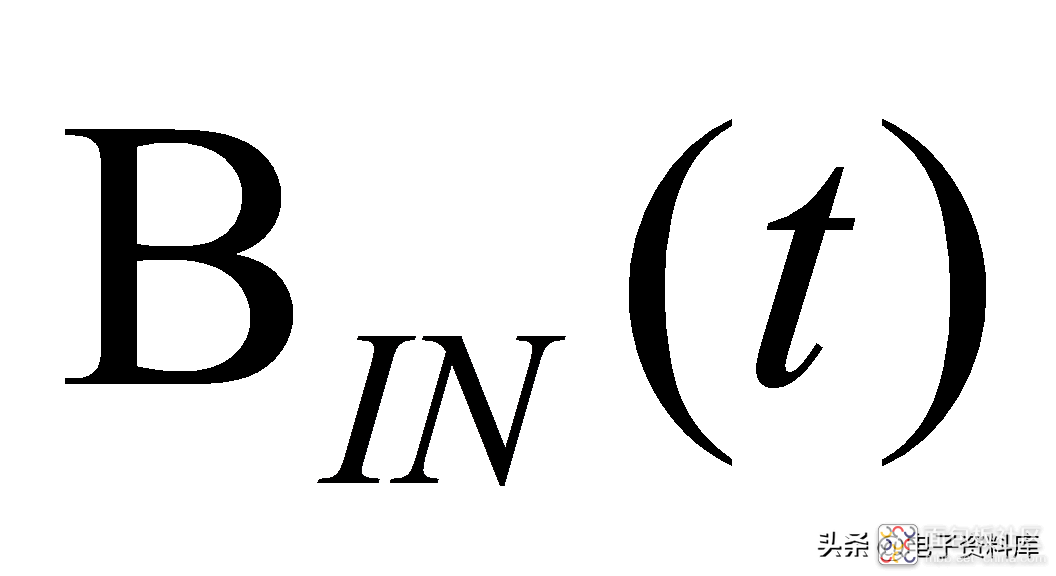
,MT910x的响应
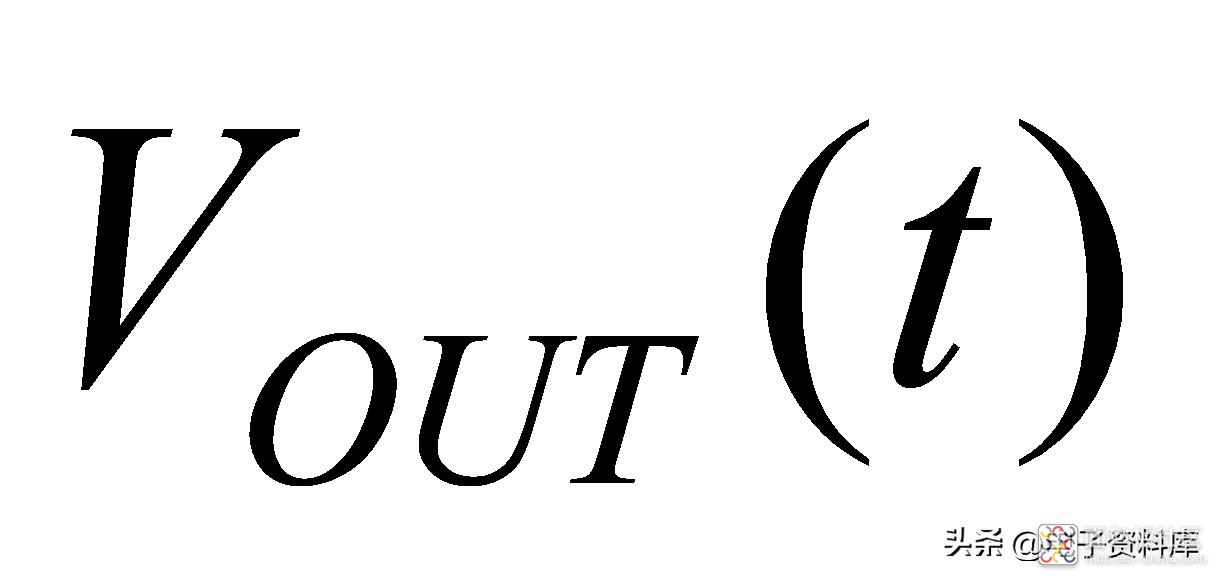
。

如图(五)所示为一个典型的采样系统:模拟输入电压信号Vin经过模数转换器(ADC)采样/量化得到Dout,Dout经过数模转换器(DAC)得到模拟输出电压信号Aout,Aout经过理想低通滤波器(LPF)滤波,便可以得到平滑后的模拟电压信号Fout。采样定律描述的便是满足什么样的条件,Fout 100%等于Vin。

根据采样定律的理论可知,要想不失真地对模拟信号进行采样,需要满足条件:采样频率Fs大于等于信号带宽的2倍。
下面就来定性的分析一下采样定律。在此之前先明确一个概念:根据信号与系统的相关理论,任何一个信号都有时域和频域两种表示方式,这两种表示方式完全等价,并可以运用傅里叶变换和反傅里叶变换相互转化。也就是说,一个信号时域波形确定了,其频谱图也就确定了,反之亦然。
如图(六)所示为采样率大于信号带宽2倍时,图(五)所示采样系统各个节点处的信号,左边的图横坐标是时间,纵坐标是幅值,表示该信号的时域波形;右边的图横坐标是频率,纵坐标是幅值,表示该信号的频谱图。
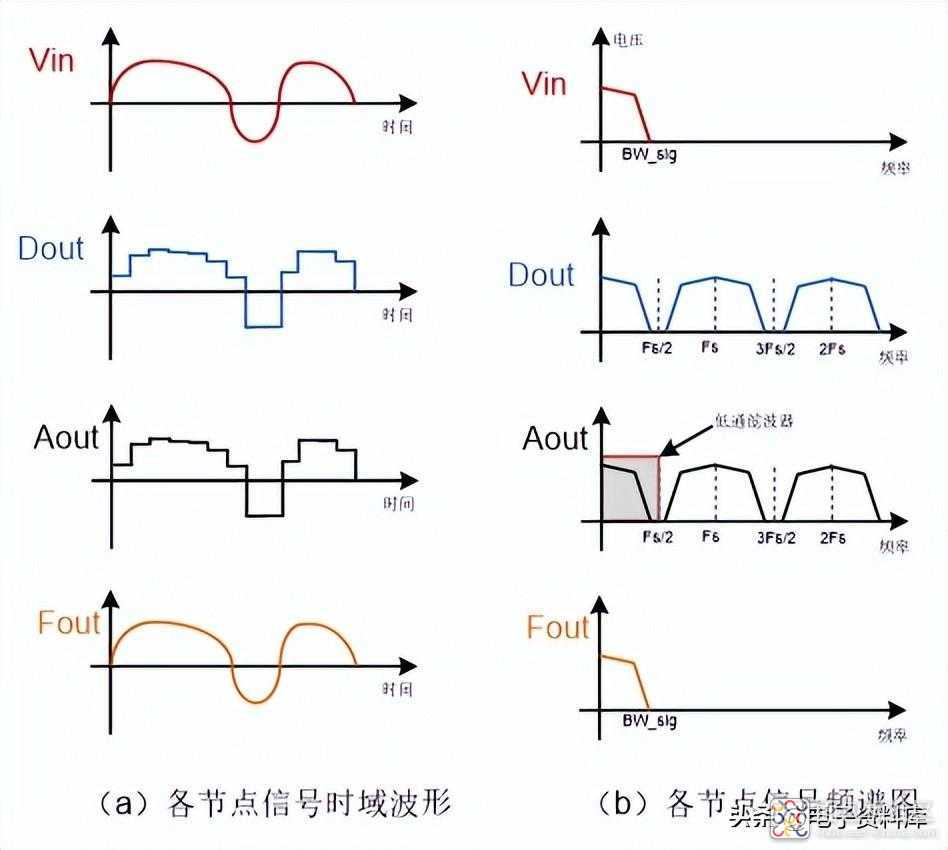
如图(七)所示为采样率小于信号带宽2倍时,图(五)所示采样系统各个节点处的信号。区别在于:
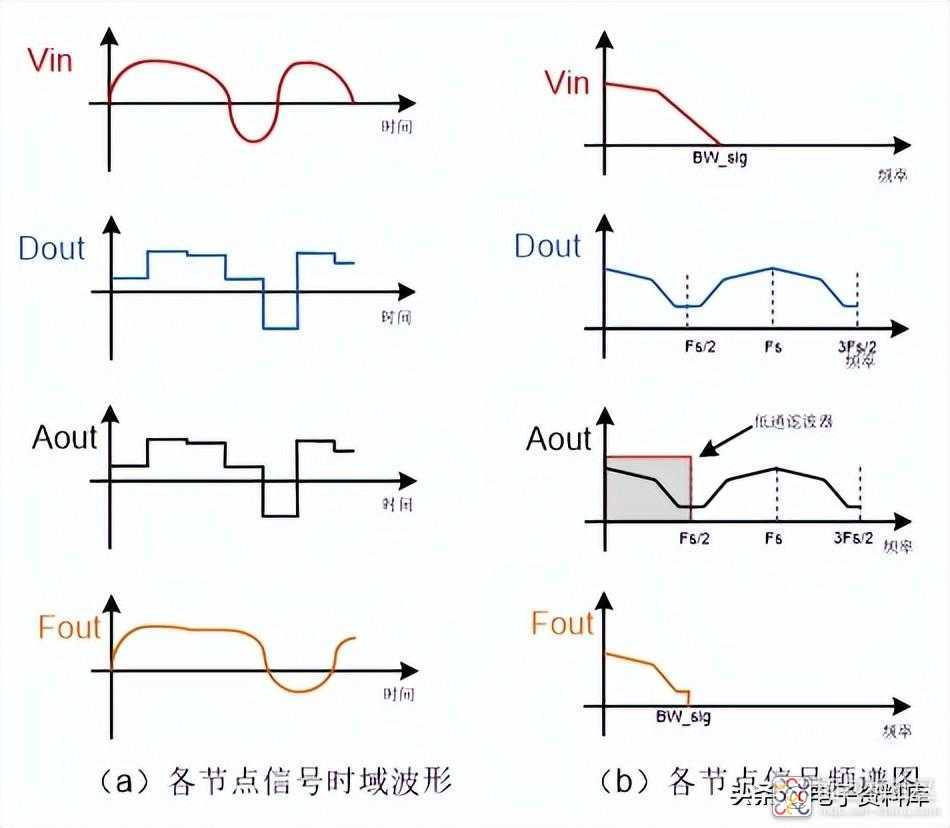
从上面分析可知:当采样率小于信号带宽的2倍时,输入信号Vin经过采样系统后无法100%还原,即信息发生丢失。
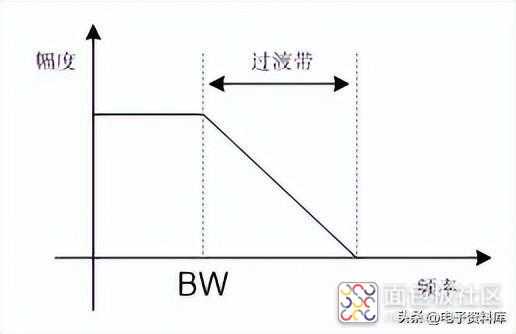
在现实中,理想的低通滤波器是无法实现的,由于实际的低通滤波器过渡带无法做到无限窄,如图(八)所示,因此为了保证不发生混频,采样率一般会远远高于2倍信号带宽。







 /5
/5 

