引言:
控制器是有源降噪系统的核心。ANC耳机的控制器可由固定控制器或自适应控制器实现,或二者兼而有之。预设计的固定控制器稳定可靠,ANC降噪量大部分由其提供。因此固定控制器设计是ANC耳机研发的关键环节,具有重要理论及实践意义。在本文中,21dB首先介绍了控制器分类、水床效应等基础知识,然后从反馈、前馈固定控制器设计两个方面分别展开,梳理了主要的研究工作。
一、控制器分类
(1)按控制结构,控制器可分为前馈及反馈控制器,两者同时存在为混馈控制器。反馈控制器又可分为内模反馈控制器与直接反馈控制器。
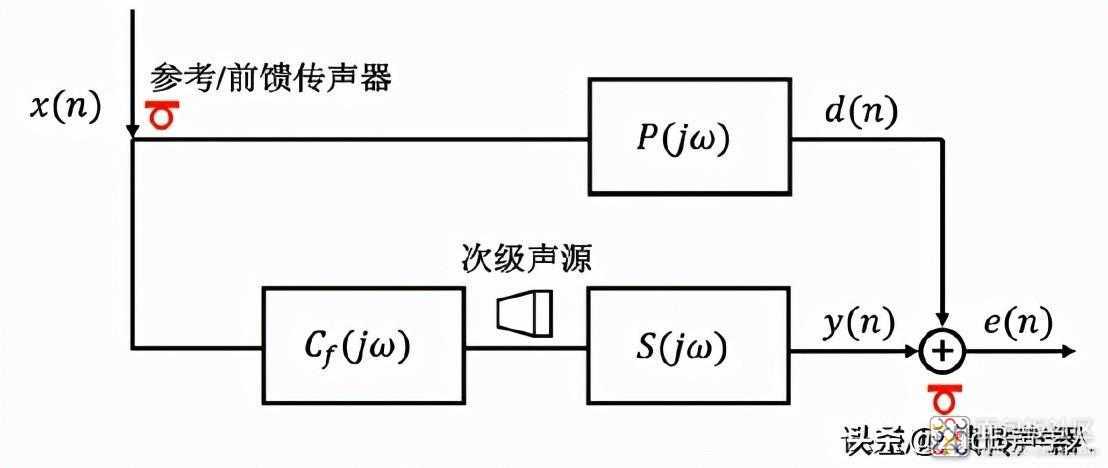
图1前馈控制结构
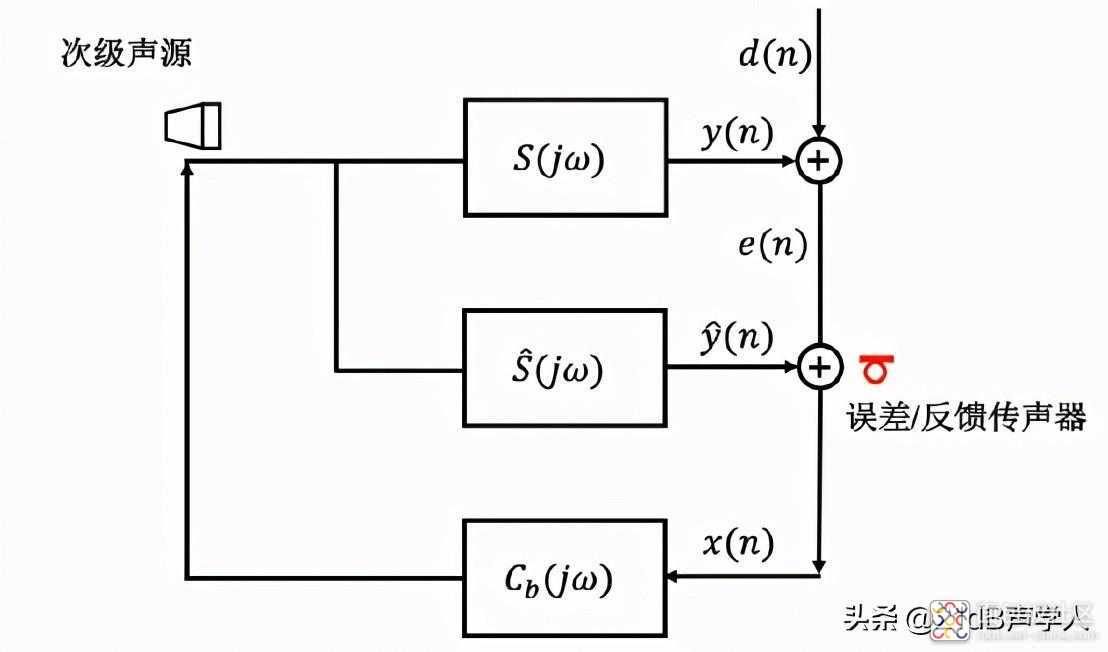
图2内模反馈结构
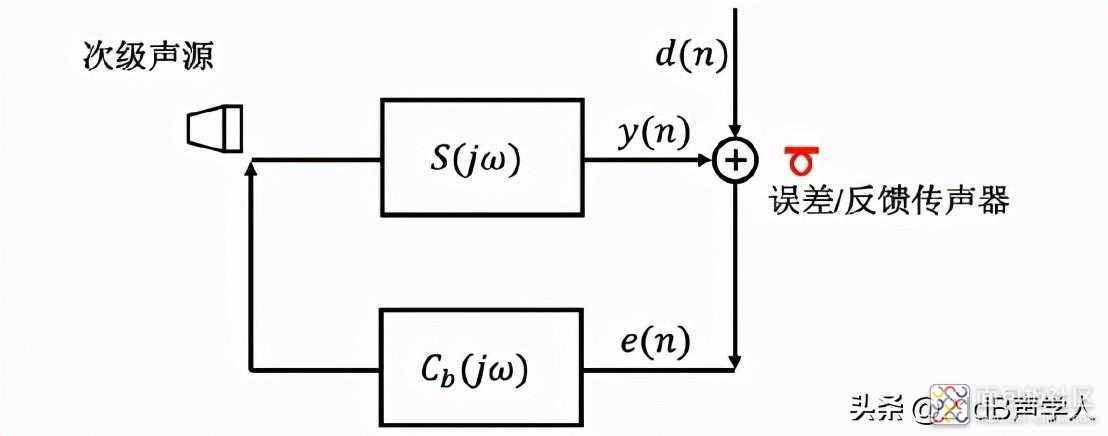
图3直接反馈结构
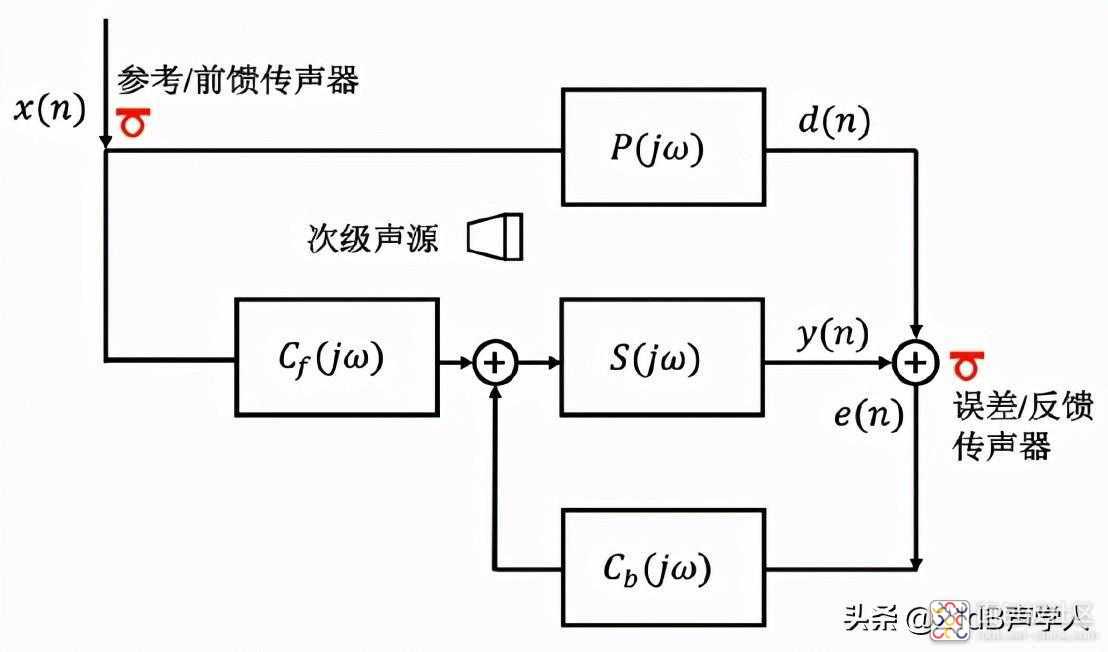
图4混馈控制结构
(2)按滤波形式,控制器可分为有限冲激响应控制器和无限冲激响应控制器,前者对当前系统输出值的预测仅受历史及当前输入的影响,不受历史输出的影响。后者对当前系统输出值的预测不仅受历史及当前输入的影响,也受历史输出的影响。
(3)按硬件实现方式,控制器可分为模拟控制器和数字控制器。在1980年以前,受电子工业发展水平的限制,控制器采用模拟电路实现,即以参数值不同的电容、电感、电阻搭配使用完成滤波。因此一旦固化定型,滤波系数便不能改变,不仅结构复杂、灵活性差、修改和升级难度大,且无法适应次级通道和外界噪声的变化。自1980年以来,随着高性能数字信号处理器(Digital signal processor, DSP)的迅速发展,其相比于模拟控制器具有灵活性高,且可自适应改变控制参数的优点,可采用模块化设计,方便调试与后续功能升级。在主动降噪耳机的应用中,控制器越来越多地采用数字控制器。
(4)按控制参数,也即滤波系数是否实时更新,控制器可分为固定控制器和自适应控制器。固定控制器的控制参数固定不变,省却因参数更新引入的频繁运算,可节省电能从而提升耳机的续航时间。自适应控制器的滤波系数可跟踪环境噪声的变化并调整,达到对时变环境噪声的良好控制。但实时更新参数,增加了计算操作数,不利于节省电能、提升续航。

二、水床效应
反馈控制系统受伯特灵敏度积分定理(Bode’s Sensitivity Integral Theorem)的限制,灵敏度函数在正频率轴的积分值等于与s右半平面极点的个数之和乘π,若反馈系统稳定,则右半平面极点个数为零。也即在反馈控制系统中,全频段的降噪量守恒且为零。若目标降噪频段在20∼1000Hz,则20Hz以下的甚低频以及1000Hz以上的中、高频均有可能取得负降噪量。
从曲线角度观察,在降噪频段正降噪量曲线越深,两侧负降噪量曲线便抬升越高。此现象仿佛水池中有一床垫,压下越深,两边水位便抬升越高一般。因此伯特灵敏度积分定理也被形象地称为“水床效应”。理想反馈固定控制器应当在降噪深度及带宽、水床抬升及鲁棒性之间取得精巧的平衡,其设计任务十分具有挑战性,但也兼具理论和商业价值,因此在过去数十年间受到了许多研究者的关注。

三、反馈控制器设计
早期对反馈控制器的设计多采用内模控制结构,内模控制也被称为Q参数模型。当内模控制器Q由FIR滤波器实现时,对滤波系数的寻优在理论上[1,2]可被证明是一个凸优化问题,因此包括序列二次规划(Sequential Quadratic Programming, SQP)在内的凸优化算法均可被应用于寻优[3,4]中。Zhang L等人[5]试图略去内模支路,以最小均方准则对反馈直接FIR控制器寻优。上述工作均能在取得一定降噪量的同时确保系统的鲁棒性。然而优化所得的FIR控制器阶数较长,致使运算操作数及寄存器空间占用均较大,限制了实际应用的前景。
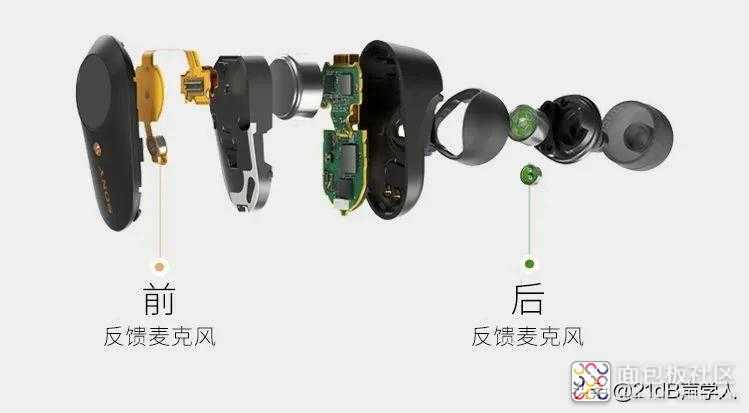
在物理上,耳机与人耳形成的腔体,可由数个级联的弱阻尼亥姆霍兹共鸣器建模。在此场景下,IIR滤波器相比于FIR滤波器更适合作为控制器[6],因为差分方程中的回归项可以高效率地对腔体中的回声信号建模,从而以较低的参数量获得高性能的控制器。且反馈控制器可采用直接控制器,结构简单无内模支路,不必计算次级噪声信号的估计值,节省运算操作数与寄存器空间占用,具有实际应用价值,因此以模拟电路[7-10]或数字电路的形式,被广泛应用于主动降噪耳机的设计实践中。然而,IIR控制器的稳定性难以保证,且因略去了内模支路,致使凸优化问题转为非凸优化问题[11],因此仅能获得次优解。若反馈控制器是通过自适应算法收敛所得,若省略内模支路、径以误差传声器拾取的信号送入控制器,最终仅能取得10dB左右的降噪量[12]。
Bai M和Lee D[7]将反馈控制器设计的次优解条件表达为线性分式变换的形式(Linear Fraction Transformation, LFT),并使用基于双Riccati方程[13]的转换矩阵方法[14]来得到兼具性能与鲁棒性的∞控制器的Riccati解。再将所得控制器的传递函数转换为单阶与二阶节级联的形式,在调整零极点位置拟合所得控制器的频响。因此这是间接优化方法,且需要细致地选取合适的权矢量来确保鲁棒性,但在设计实践中难度较大。
Yu S H和Hu S J[15]曾使用递归二次规划(Recursive Quadratic Programming,RQP)搜索IIR控制器的滤波矢量, 的次优解。然而对于直接型IIR滤波器,需要提取其极点半径并施加约束,因此Lienard-Chipart准则被用于确保控制器的稳定,这增加了优化问题的复杂性。Seo J H等人[16]尝试先设计高阶的内模FIR控制器,再使用平衡模型截断(Balanced Model Truncation, BMT)近似和频率弯折(Frequency Warping)技术,用级联双二阶IIR滤波器来替换FIR控制器。这也是间接的设计方法,虽然回避了直接设计方法引入的非凸优化难题,但不完美的转换致使降噪量产生了一定程度的损失。

作为生物/自然启发式群体智能算法的典型代表,遗传算法(Genetic Algorithm, GA)[17]已被应用在非线性有源噪声控制中,代替滤波X算法(Filtered-X Algorithms)来实时更新控制器的滤波系数,且不需要针对次级通道进行预先建模,同时可以避免滤波X算法可能导致的局部最优问题。使用遗传算法的代价是,参数量和计算量均很大。Nelder-Mead单纯形算法(Nelder-Mead Simplex Method)[18]凭借其较好的无梯度局部优化能力,已被应用在有源噪声控制中,根据设定的性能准则调整控制器参数。Kataja J等人[19]曾使用遗传算法和NM算法来分别优化固定反馈控制器中二阶节的参数。由于NM优化器的优化结果高度依赖初始解,因此它需要以随机生成的初始解运行数次求解。遗憾的是,遗传算法本可以为NM优化器提供初始解,但仅被用来做对比。类似的两阶段组合优化策略已被应用在有源噪声控制中[20]。然而,Kataja J等人的工作中并未针对鲁棒性给出约束条件,可能会致使所得优化结果幅度及相位裕度不足。
Wang J J等人[21]提出了一种综合优化框架,反馈控制器由恒稳定的参数化二阶节(低架滤波器、峰化滤波器)级联而成,基于传统的2/∞优化思想,以自设计的惩罚函数将水床抬升及系统鲁棒性作为惩罚项,与灵敏度函数(降噪量的逆)合并构成总的目标函数,并使用遗传算法加单纯形算法组合而成的两阶段优化算法搜索控制器的全局次优解,以遗传算法克服优化问题非凸性,再以单纯形算法精调控制器参数。其仿真及实验结果表明,该优化框架可取得优异反馈降噪量,同时保证系统的鲁棒性。
四、前馈控制器设计
不同于反馈控制器设计,前馈控制器存在理论最优解[22],为主噪声路径与次噪声路径的比的负值。因此其设计问题可被转化为控制器拟合问题,即以控制器的滤波系数为输入变量,以最小化某种准则下对生成的控制器与理想控制器频响之间的误差为目标。但这种目标函数的构建方式没有与降噪量直接关联起来,是间接设计方法。因此需推导出前馈灵敏度函数以预测理论降噪量,据此调节前馈控制器参数,来最小化前馈灵敏度函数(最大化前馈降噪量),并压制由于生成的前馈控制器与理想控制器频响失配导致的降噪量反抬(在反馈中被称为水床抬升)。Wang J J在其硕士毕业论文中在分析同频不等幅信号干涉原理的基础上,推导出了前馈灵敏度函数,并给出了目标函数的设计准则及理论与实验结果。
五、讨论
1.反馈控制中控制点与目标降噪量不匹配的问题
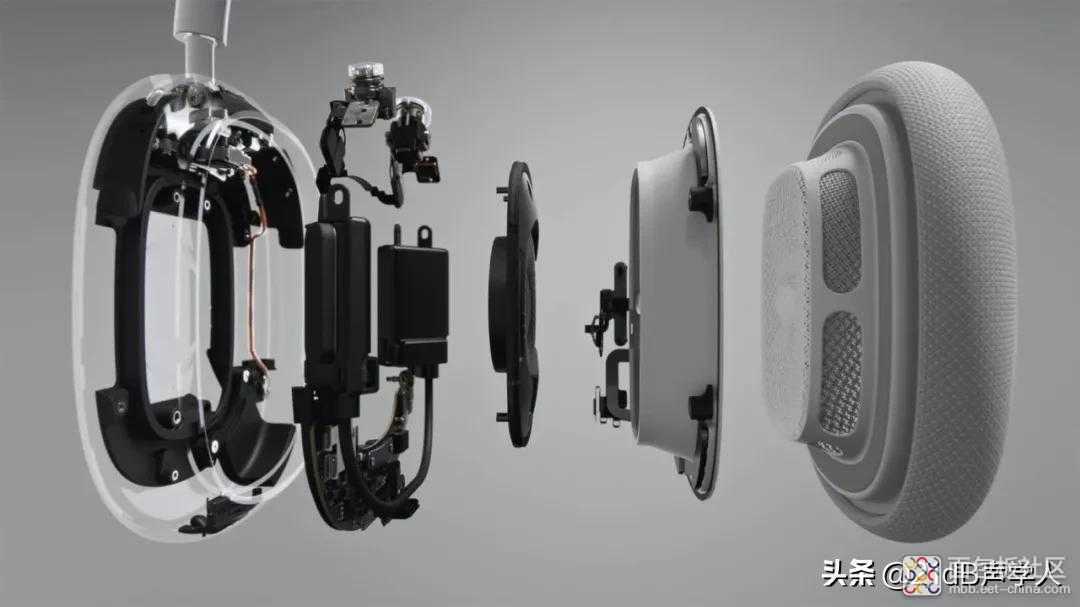
前馈灵敏度函数的观察点在虚拟误差传声器(也即鼓膜)处,前馈降噪量即是鼓膜处的降噪量。但在所有历史工作中,反馈灵敏度函数的观察点都是物理误差传声器(也即耳机的反馈传声器)处,并非在鼓膜处。于耳塞式耳机而言,耳机反馈麦与鼓膜相距较近,且都在耳道内,物理次级通道(耳机扬声器至物理误差传声器)与虚拟次级通道(耳机扬声器至虚拟误差传声器)频响差异不大,因此反馈灵敏度函数在反馈麦与鼓膜处的差异不大,反馈麦处取得的降噪量可大体表征鼓膜处的降噪量,但是对于耳罩式耳机,物理次级通道与虚拟次级通道的差异较大,不便用反馈麦处取得的降噪量来表征鼓膜处的降噪量,必须对原来的灵敏度函数加入修正,Wang J J在其硕士毕业论文中给出了相关推导与修正之后的目标函数。
2.次级通道(无论物理还是虚拟)频响随佩戴松紧度变化的问题
在真实使用时,由于人头大小、耳道口形状因人而异,因此无论对于耳塞式还是耳罩式耳机,次级通道频响都会发生变化。从而影响实际使用时的反馈及前馈降噪量。如图5,展示了耳机佩戴在16名受试者头上时所测次级通道频响的差异,幅频响应曲线的差异主要体现在400Hz以下的低频,幅度差异可达10dB,相频响应曲线的差异主要体现在 700 Hz 以下的低频,相频差异可达50°。频响曲线分化出差异的原因在于受试者头的大小、宽窄各不相同,当受试者佩戴头带式耳机时,头带长度各不相同,耳罩对耳周的压力也各不相同,因此所形成的共振腔共振强度也不同。图中红色箭头指明了随幅频曲线变化,相位曲线的变化趋势:在低频,随幅频曲线降低,共振强度变弱,相频响应曲线的平直度变好,控制器拉高增益即可取得降噪量,而不需要修正相位来达到完美的相消干涉条件,这有利于反馈固定控制器的设计。
对此一种解决方案是预设计多组前、反馈控制器,在实际佩戴时通过发射辨识音效声确定佩戴状况,从而在预设计的控制器组中挑选针对此种佩戴状况降噪量最佳的那一组控制参数,从而达到应对不同人、应对同一人的多次佩戴等多种因素下也能降噪量始终优秀的控制效果。这被称为自适应泄露补偿(Adaptive Leakage Compensation, ALC)技术。实际上,恒玄科技童伟峰等人在2020年初即有相关专利公布[23]。辨识可以佩戴上后立即发一声音效声(许多厂家都这么做),也可以在耳机播放音乐时利用音乐本身来在线辨识次级通道频响(即是苹果所谓的200Hz在线自适应均衡)。辨识共振腔强度仅需获知400 Hz以下低频的回声强度,并不需要做全频段的次级通道辨识,因此选取能量主要集中在低频的音效声即可满足实际应用需求。
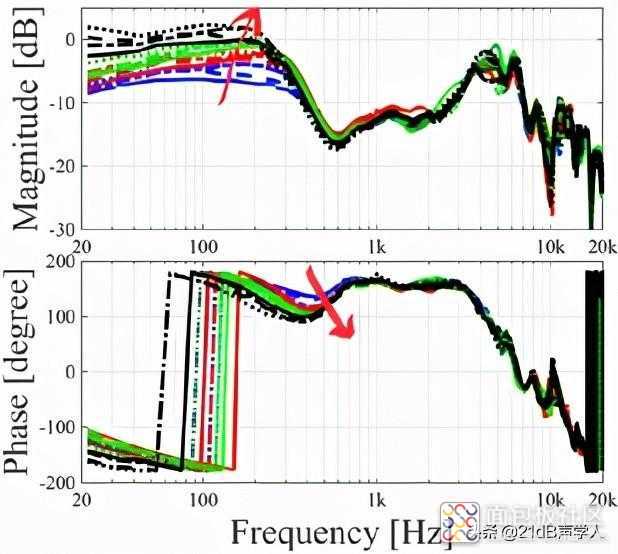
图5不同受试者佩戴同一耳罩时的物理次级通道频响
参考文献:
[1] Boyd S P, Balakrishnan V, Barratt C H, et al. A new cad method and associated architectures for linear controllers [J]. IEEE Transactions on Automatic Control, 1988, 33(3): 268-283.
[2] Helton J W, Sideris A. Frequency response algorithms for ∞ optimization with time domain constraints [J]. IEEE Transactions on Automatic Control, 1989, 34(4): 427-434.
[3] Rafaely B, Elliott S J. 2/∞ active control of sound in a headrest: design and implementation [J]. IEEE Transactions on Control Systems Technology, 1999, 7(1): 79-84.
[4] Bai M R, Zeung P. Synthesis of a robust broadband duct anc system using convex programming approach [J]. The Journal of the Acoustical Society of America, 2002, 111(4): 1751-1757.
[5] Zhang L, Wu L, Qiu X. An intuitive approach for feedback active noise controller design [J].
Applied Acoustics, 2013, 74(1): 160-168.
[6] Elliott S J. Signal processing for active control [M]. Elsevier, 2000.
[7] Bai M, Lee D. Implementation of an active headset by using the ∞ robust control theory [J]. The Journal of the Acoustical Society of America, 1997, 102(4): 2184-2190.
[8] Pawełczyk M. Analogue active noise control [J]. Applied Acoustics, 2002, 63(11): 11931213
[9] Pawelczyk M. Analog active control of acoustic noise at a virtual location [J]. IEEE Transactions on Control Systems Technology, 2008, 17(2): 465-472.
[10] Liang K W, Hu J S. An open-loop pole–zero placement method for active noise control headphones [J]. IEEE Transactions on Control Systems Technology, 2016, 25(4): 1278-1283.
[11] Boyd S P, Barratt C H. Linear controller design: limits of performance [M]. Prentice Hall Englewood Cliffs, NJ, 1991.
[12] Wu L, Qiu X, Guo Y. A simplified adaptive feedback active noise control system [J]. Applied Acoustics, 2014, 81: 40-46.
[13] Doyle J, Glover K, Khargonekar P, et al. State-space solutions to standard 2 and ∞ control problems [C]//1988 American Control Conference. IEEE, 1988: 1691-1696.
[14] Tsai M C, Tsai C S. A transfer matrix framework approach to the synthesis of ∞ controllers [J]. International Journal of Robust and Nonlinear Control, 1995, 5(3): 155-173.
[15] Yu S H, Hu J S. Controller design for active noise cancellation headphones using experimental raw data [J]. IEEE/ASME Transactions on Mechatronics, 2001, 6(4): 483-490.
[16] Seo J H, Youn D H, Park Y C. A method of designing low-power feedback active noise control filter for headphones/earphones [J]. The Journal of Korea Institute of Information, Electronics, and Communication Technology, 2017, 10(1): 57-65.
[17] Bagley J D. The behavior of adaptive systems which employ genetic and correlation algorithms: technical report [R]. 1967.
[18] Nelder J A, Mead R. A simplex method for function minimization [J]. The Computer Journal, 1965, 7(4): 308-313.
[19] Kataja J, Kääriä A, Antila M. Optimisation of digitally adjustable analogue biquad filters in feedback active control [C]//Proc. Forum Acusticum. 2005: 861-864.
[20] Raja M A Z, Aslam M S, Chaudhary N I, et al. Design of hybrid nature–inspired heuristics with application to active noise control systems [J]. Neural Computing and Applications, 2019, 31(7): 2563-2591.
[21] Wang J , Zhang J , Xu J , et al. An optimization framework for designing robust cascade biquad feedback controllers on active noise cancellation headphones[J]. Applied Acoustics, 2021, 179(3):108081.
[22] Latos M, PAWEŁCZYK M. Feedforward vs. feedback fixed-parameter 2 control of nonstationary noise [J]. Archives of Acoustics, 2009, 34(4): 521-535.
[23] https://wenku.baidu.com/view/8d4e0f03acaad1f34693daef5ef7ba0d4b736ddb.html
来源:21dB声学人 中科院声学所苏州电声产业化基地旗下科技媒体 





 /5
/5 


