什么是开关电容
我们之前说到的滤波器,他们的特征是 和 都受控于元件比值,而 同时受控于元件的乘积,虽然可以通过采用温度和时间有良好跟踪能力的器件使比值保持住,但是却很难对乘积进行控制。
如果要在一块芯片上同时实现滤波器功能和数字功能,那么构建滤波器的元件就必须使用MOS晶体管和小MOS电容。这种限制条件就促使了开关电容(SC)滤波器的发展。该滤波器通过MOSFET开关周期性地作用于MOS电容来模仿电阻。而它的时间常数依赖于电容的比值而不是RC乘积。
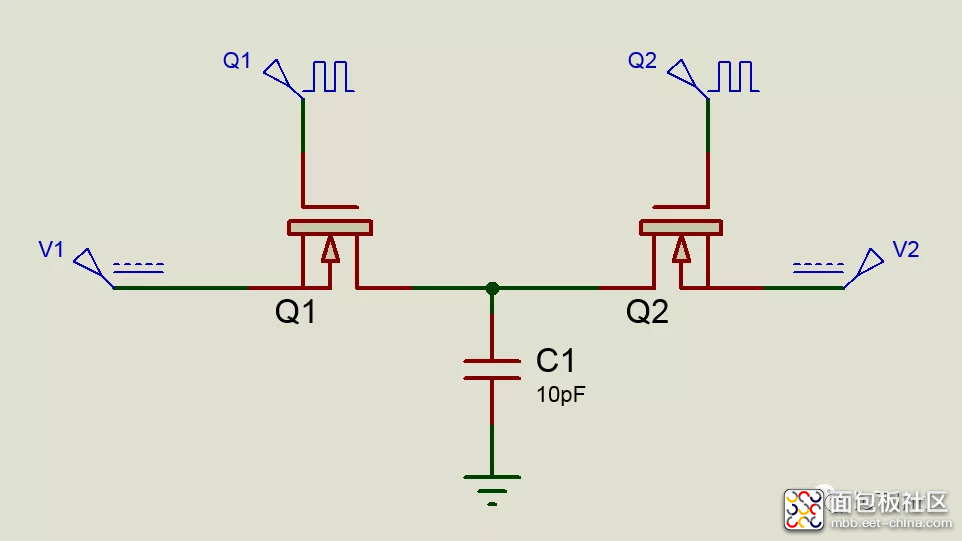
如上图所示的MOSFET电容电路来说,图中的晶体管属于N沟道晶体管,晶体管在导通的时候内阻很低,而没导通的时候内阻很高,因此MOSFET常常作为开关来使用,试想下,如果在两个mosfet的G极分别以半个周期交替导通,如此可以实现单刀双掷SPDT开关函数。
假设V1>V2,同时Q1导通,可以将电容C充电到V1,然后将Q2导通,电容C放电到V2,那么这个过程从V1到V2转移的总电荷为 ,如果Q1和Q2交替导通的频率为f,那么可以由在1秒内从V1到V2转移的电荷量来定义平均电流
假设V1>V2,同时Q1导通,可以将电容C充电到V1,然后将Q2导通,电容C放电到V2,那么这个过程从V1到V2转移的总电荷为 ,如果Q1和Q2交替导通的频率为f,那么可以由在1秒内从V1到V2转移的电荷量来定义平均电流
如果进一步变换这个等式
可以看出,开关电容组合可以用一等效电阻来表示。
SC积分器
前面又说到RC积分器基于OP放大器的有源模拟滤波器设计--一阶有源滤波器有说到传递函数 ,其中
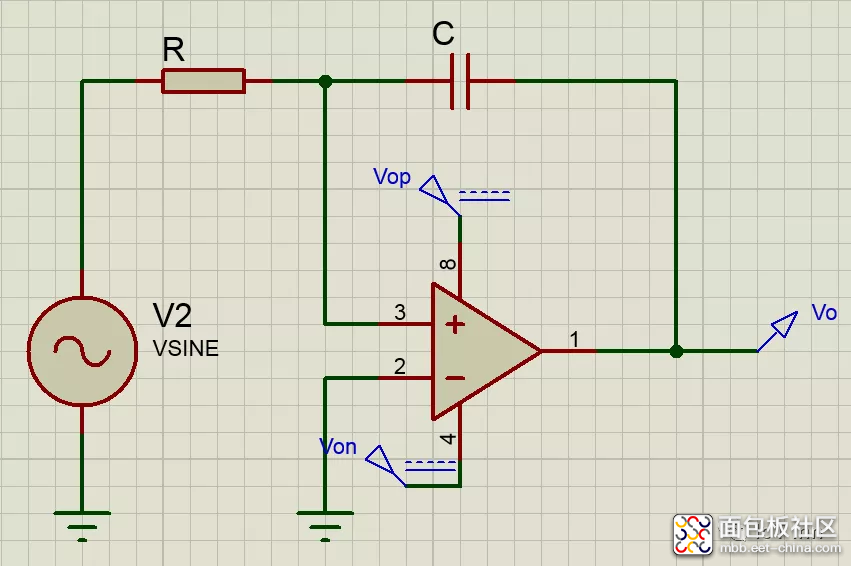
如果用一个SC电阻代替R,同时输入频率 满足 ,结合上面说的等效电阻的公式可以得出:
其中C1为等效的开关电容。从上面的表达式可以得出如下结论:
1、电路中没有电阻,这就避免了电阻的容差和热漂移带来的困扰。另外实现开关功能的MOSFET使用的基本元件占用的面积比单片电阻占用的面积小
2、特性频率 取决于电容的比值。这种形式随着温度和时间变化进行控制和保持, 比RC的乘积形式容易的多
3、特性频率 与时钟频率 成比例,表明SC滤波器必然是可编程类型。改变时钟频率会在频谱图上使响应上移或下移。另一方面,如果需要一个固定和稳定的特性频率,则可以用一石英晶体振荡器来产生时钟频率。
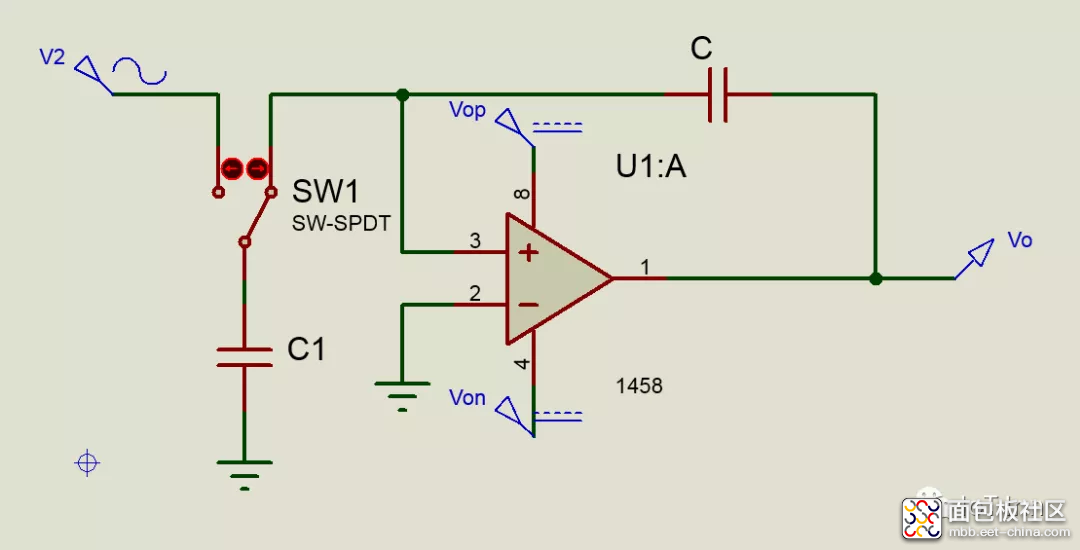
为了减小分布电容的影响以及增加电路的通用性,可以用SPDT开关对来组成实际的SC积分器,下图中,将开关拨到下方是C1放电至零,而使开关拨到上方则会对C1充电至Vi,如果Vi>0,电流因此会流到放大器的求和节点,如果Vi<0,则会流出,这表明该积分器是反相器。
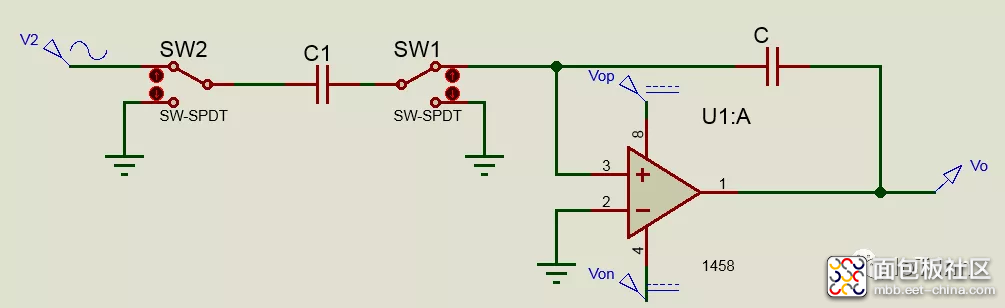
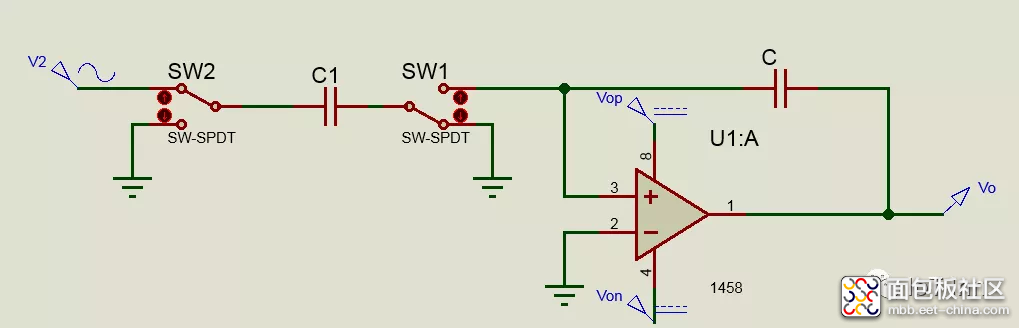
SC双二阶滤波器
双积分环路滤波器
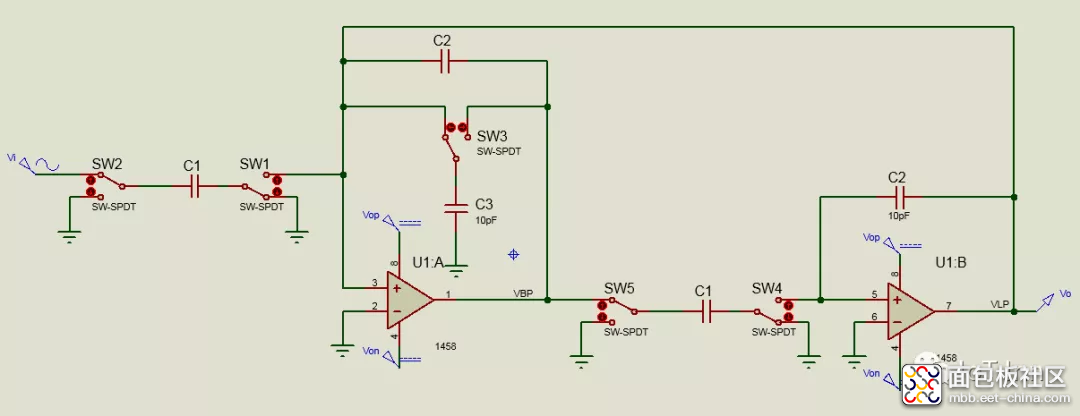
通过U1:A同相节点,在 的情况下,电流求和可得:
其中 ,整理可得 :和
其中 和 是标准的二阶低通和带通响应。且
假设电路中 ,如果要实现f0=1KHZ的巴特沃兹低通响应,且满足总电容值等于或小于100pF。计算如下,由已知可得C2/C1=fsc/(2πf0)=15.9和C3/C1=1/Q= ,选择C1=1pF,C2=15.9pF和C3=1.41pF,即可实现。
上面的电路会随着Q值的增加使得电容分布增加,直至这种电路不可行。为了改善这种情况,可以使用一个积分器或者加法器和一个同相积分器来产生带通和高通响应。
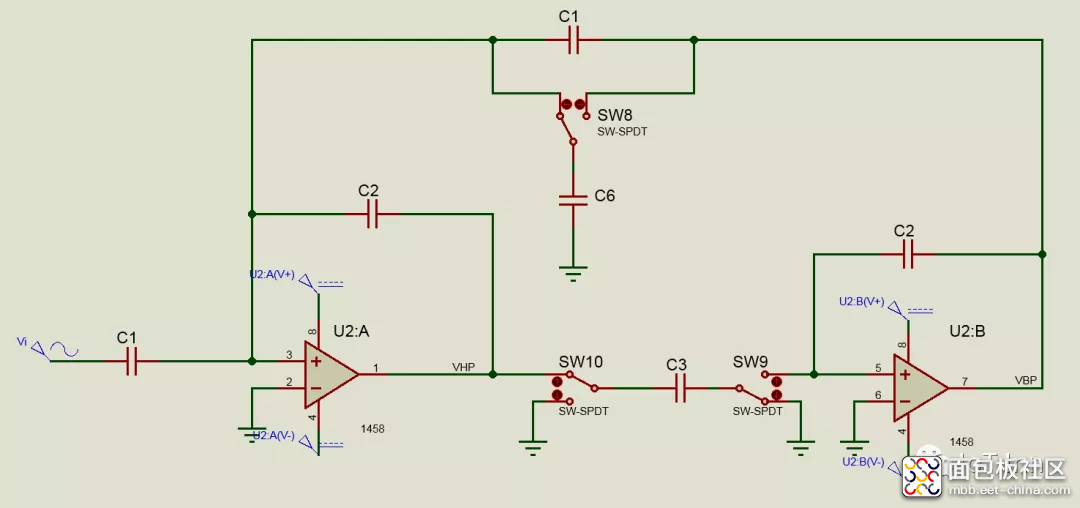
同理,在节点电流求和可得:
可以看出改善后的电路对电容比值有所改善。
内容转载自 网络,仅供学习交流使用,如有侵权,请联系删除。






 /4
/4 

