拉氏变换是一个线性变换,可将一个有参数实数t(t≥ 0)的函数转换为一个参数为复数s的函数。
拉普拉斯变换在许多工程技术和科学研究领域中有着广泛的应用,特别是在力学系统、电学系统、自动控制系统、可靠性系统以及随机服务系统等系统科学中都起着重要作用。
拉普拉斯变换的公式
拉普拉斯变换是对于t≥0函数值不为零的连续时间函数x(t)通过关系式
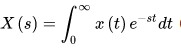
(式中-st为自然对数底e的指数)变换为复变量s的函数X(s)。它也是时间函数x(t)的“复频域”表示方式。
电路分析实例
据此,在“电路分析”中,元件的伏安关系可以在复频域中进行表示,即电阻元件:V=RI,电感元件:V=sLI,电容元件:I=sCV。如果用电阻R与电容C串联,并在电容两端引出电压作为输出,那么就可用“分压公式”得出该系统的传递函数为H(s)=(1/RC)/(s+(1/RC)),于是响应的拉普拉斯变换Y(s)就等于激励的拉普拉斯变换X(s)与传递函数H(s)的乘积,即Y(s)=X(s)H(s)
如果定义:f(t)是一个关于t的函数,使得当t<0时候,f(t)=0;s是一个复变量;
则 f(t)的拉普拉斯变换由下列式子给出:
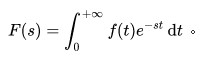
拉普拉斯逆变换
拉普拉斯逆变换是已知F(s) 求解 f(t) 的过程。用符号
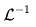
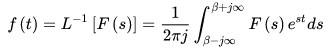
我们在实际中进行拉氏逆变换的时候,一般的做法是,通过列表的方式给出了一些像函数所对应的原函数,我们通过部分分式展开法将像函数化作几个分解为若干个表中所有或者容易查到的简单变换式之和。









 /2
/2 

