电路有数字和模拟之分,信号同样也有。模拟即为连续,数字则是离散,这里的连续和离散包括两方面:一为取值离散/连续,一为时间离散/连续。我们知道计算机的数据是由0和1组成的数字信号,而我们生活的世界是模拟的,我们眼睛看到的运动、气味的扩散、声音的传播等都是连续的、模拟的。电脑要捕捉实际环境中的模拟信号,而转化成数字信号,最后加工处理。这个过程把模拟信号变成数字信号,实现这个过程的器件即为ADC。
在应用中,我们通常见不到独立的ADC芯片,多数都集成在处理器、平台或者模块内。也因此,硬件工程师似乎对ADC的关注度似乎并没有其他那么高。但作为一个采集信息的硬件电路,并不应该被我们所忽略。
一、信号采样与量化
之前提到过,模拟就是在时间和值上边的连续信号。图1的系统曲线即为一段模拟信号,横坐标t为时间,纵坐标表示幅度。我们可以看到,这段曲线不论在时间上还是在取值上边都是连续变化的模拟信号。
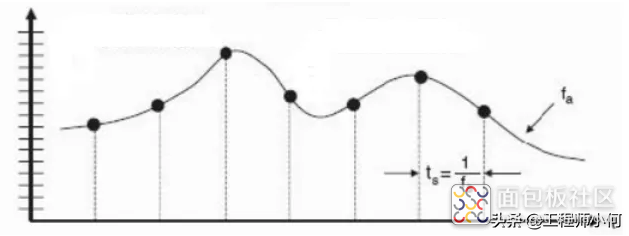
图1 系统曲线及采样
我们知道,处理器处理的是离散信号,因此就要对这段连续的模拟信号进行采样,在每一个固定的时间间隔ts内取点,读取该点在该时刻的值,于是就形成了一组离散数据。这时,固定的时间间隔ts称为采样周期。把连续时间通过采样周期分隔开的过程叫做采样过程。通过采样周期,把连续数据变成离散数据的过程,叫做信号的量化。
图1中,每间隔ts时间取到的线上的黑点,即为量化后该信号的离散信号。整个过程,则是模拟信号转为数字信号的过程,即为A/D转换。如此,ADC的结构图大体可以总结如下:

图2 ADC结构示意图
不难发现,随着采样周期ts的不同,量化后的信号则会不同。ts越小,即采样频率越高,则被采样本越多,相应的信号变形越小,越逼近于实际的模拟信号。ts越大,采样频率越低,采样样本越少,就会出现重要数据的丢失。我们看一个例子:
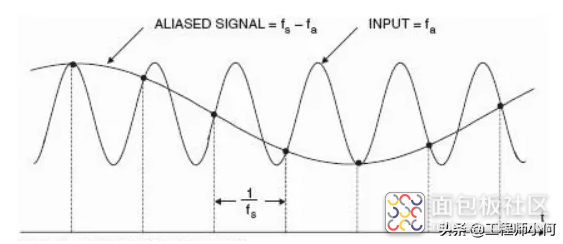
图3 采样周期
如图3,我们需要采样的INPUT信号为频率为fa的正弦信号,当我们选取采样周期为1/fs时,可以得到一组量化的数据信号。当我们把这组数据信号进行连线表示出来后,则得到ALIASED的信号。我们发现经过量化再现的信号跟原来的模拟信号比完全不同,出现了另外一种形式的信号。
因此采样周期的选取决定了信号是否会失真。经典的奈奎斯特定律,又为香农采样定律被提出。简单地说,要求采样频率至少是被采信号频率(带宽)的两倍以上,否则就会出现信息丢失。
二、ADC的类型
根据ADC转换原理,可以分为并行比较型ADC、双积分型ADC、逐次逼近型ADC以及∑-Δ型ADC。
来源:《硬件女工程师的日常》手机射频驿站







 /5
/5 


