蒙特卡洛(Monte Carlo)模拟是以概率统计原理为基础,
模拟自变量的随机变化,算出由这些自变量所导致的其它因变量的数值,
并对结果进行统计分析,研究其分布规律,以达到认识事物特征及其变化规律的方法。
在对一些复杂电子电路进行分析计算时,
我们通常很难根据电子、电路理论得到电压、电流、功率等电气参数的解析解。
即使得到了解析解,我们很难分析因变量与自变量的极值关系,
因而无法得到各电气参数的最大、最小值,无法对其可靠性进行有效评估;
根据中心极限定理,一个由多个随机变量组成的整体分布为高斯分布,与多个随机变量的分布形式无关。
蒙特卡洛采用随机行走的方法,以某种概率分布(一般以均匀分布即可)的方式在一定范围内随机设定各元器件的性能参数,并计算出分析参量值。
尽可能多得重复该随机过程,对得到的分析参量进行统计分析,得到参量的分布情况,
以3倍的标准差所对应的分析参量值(相对为97.3%的概率分布),并将此值当作最坏情况对应的参量值。
圆周率的计算
如下图所示,一个圆位于正方形内部,并与正方形相切;
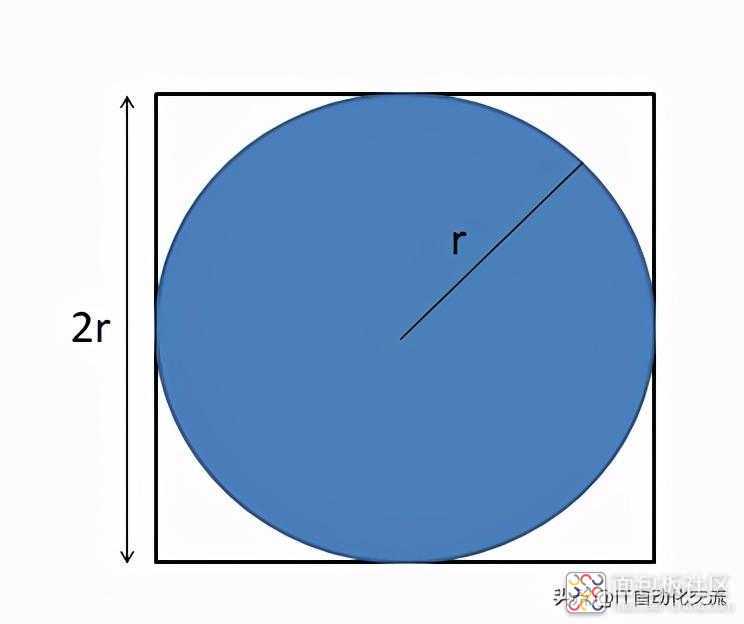
圆与正方形相切
圆和正方形的面积之比是π/4。
在这个正方形内部,随机产生n个点(这些点服从均匀分布),
计算它们与中心点的距离是否大于圆的半径,
以此判断是否落在圆的内部。统计圆内的点数,
与n的比值乘以4,就是π的值。
理论上,n越大,计算的π值越准。
PS: 自几年前起,matlab6.5不能在64位系统上安装,matlab2010R需要license,
我就失去了matlab这一科研利器,对复杂计算就累觉不爱了。
没有了matlab,我用excel采用蒙特卡洛来计算圆周率,步骤如下:1) 采用rand函数产生两组N个随机数,分别放于A列单元格以及B列单元格,一组计为x,另一组计为y;
2) 在c列单元格中,以公式sqrt(power(a2-0.5,2)+power(b2-0.5,2)),计算每一个(x,y)与圆心(0.5,0.5)的距离;
3)在d列单元格中,以公式if(c2<=0.5,1,0)对位于圆内的点进行映射,位于圆内的映射为数值1,否则映射为0。
4)对d列进行求和,得到的值就是位于圆内的点的个数M,
5)圆内的点数/总的点数=圆的面积/正方形的面积=π/4,得到π=4*圆内的点数/总的点数。

利用excel进行蒙特卡洛模拟
当N取5000时,算出π=3.127826
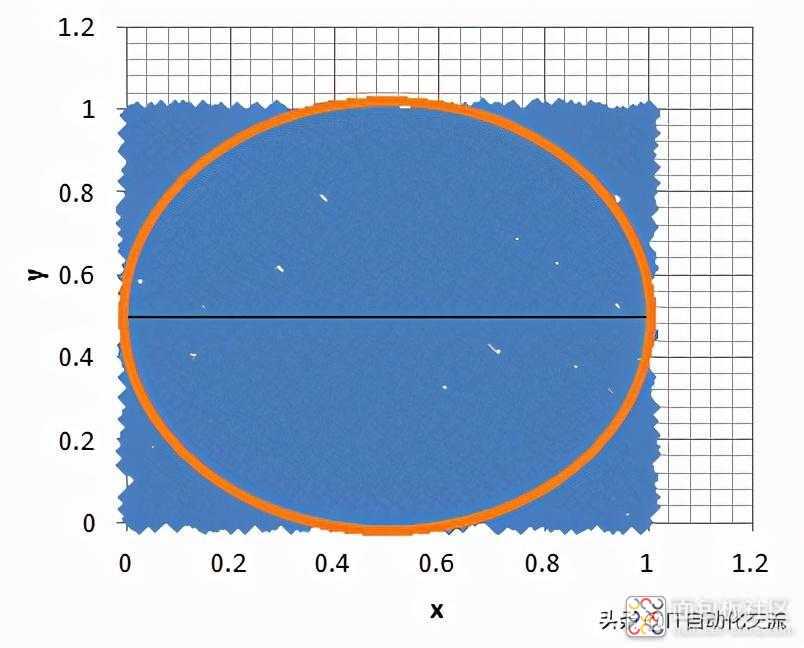
5000个随机点得到的x,y分布
当N取100000时,算出出π=3.14248。
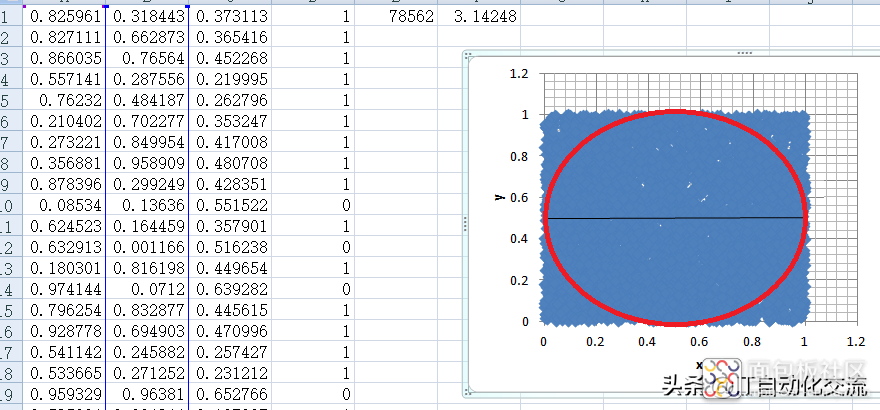
N=100000
随机点数越多,计算得到的π越准确。
电路可靠性分析在上一篇文章中,我分析了一个用于数码管LED驱动的电路,如下图:
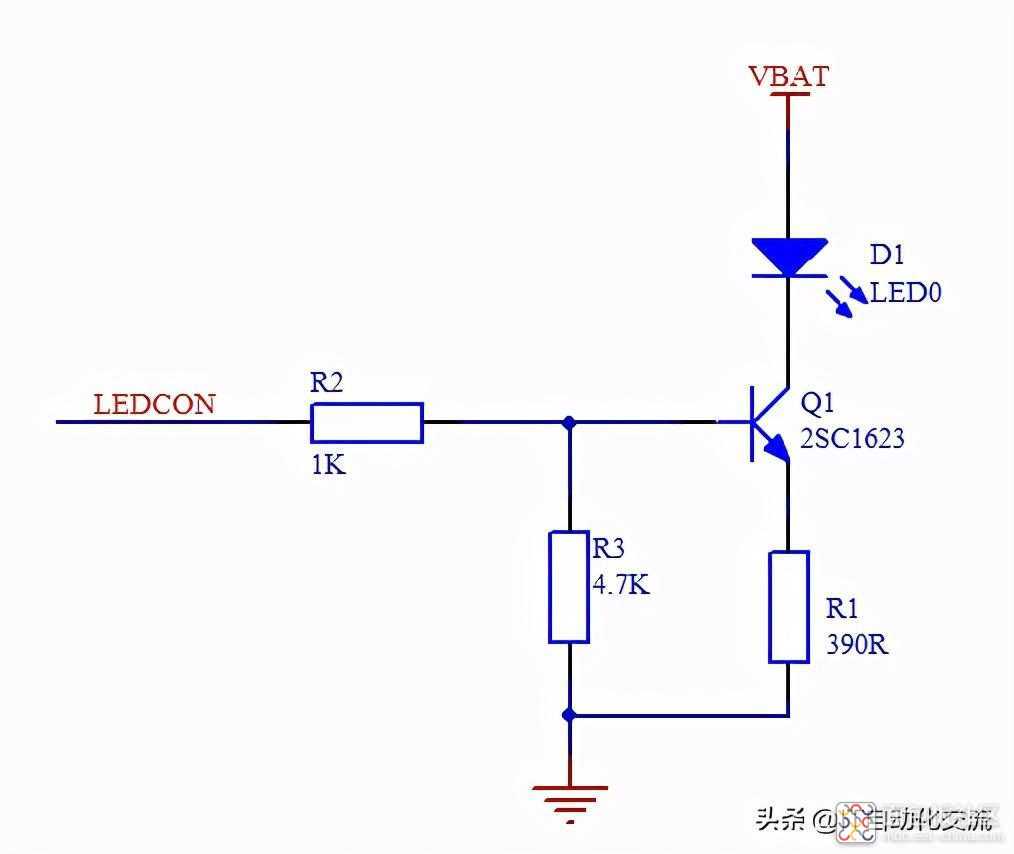
用于数码管驱动的射极跟随电路
分析得到三极管Q1的基极的电流计算公式:
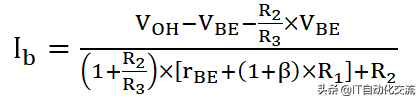
Q1的基极电流公式
式中,VOH是5.0V供电的单片机的输出高电压;
VBE是三极管Q1的B、E极导通电压;
β三极管Q1的电流放大倍数;
通过一些简化,算出流过LED的电流是一个恒定值,典型值大概为10mA。
但是并没有算出一些极限参数,不知道在其它电参数变化时,是否还保持恒定。
另外,未能三极管最大功率,不知道其是否能稳定工作,等等。
进一步计算,我们还可以得到流过LED的电流为:
Ic=β*Ib;
Q1的功耗为:P=(VBat-(β+1)*Ib*R1-VLed)*β*Ib。
其中,VBat为电池电压,VLed为LED的导通电压;
我们接下来在两个方面对I和P进行可靠性分析:
1) 流过LED的电流最大值、最小值,确认其能保持恒定;
2) 三极管Q1在极限情况下的最大功耗,确保其不超过允许的最大功耗。
在上述分析时,根据规格书,我们知道与之相关的参数的取值范围:
VOH:4.8V-5.2V;
VBE:0.3V-0.9V;
R1:351Ω-429Ω;
R2:0.9kΩ-1.1kΩ;
R3:4.23kΩ-5.15kΩ;
β:30-150;
VLED:1.8V-2.5V;
VBat:9V-16V;
假设,这些变量都是独立不相关,而且其取值都在规格范围内随机分布的。采用excel生成N组各变量的随机数,计算Ic和P:
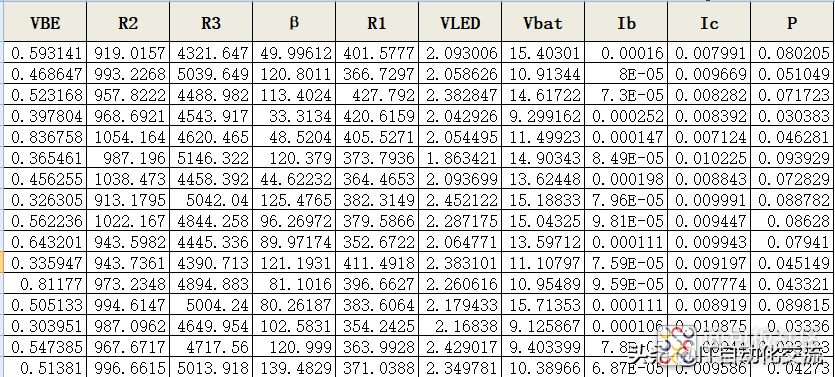
采用excel进行电路monte carlo分析
取N=100000,得到流过LED的电流最大值为11.11mA,最小值为6.46mA。
三极管Q1的功耗最大值为112mW,最小值为24mW。
利用frequency函数对结果进行分区间统计,并绘制分布图,如下:
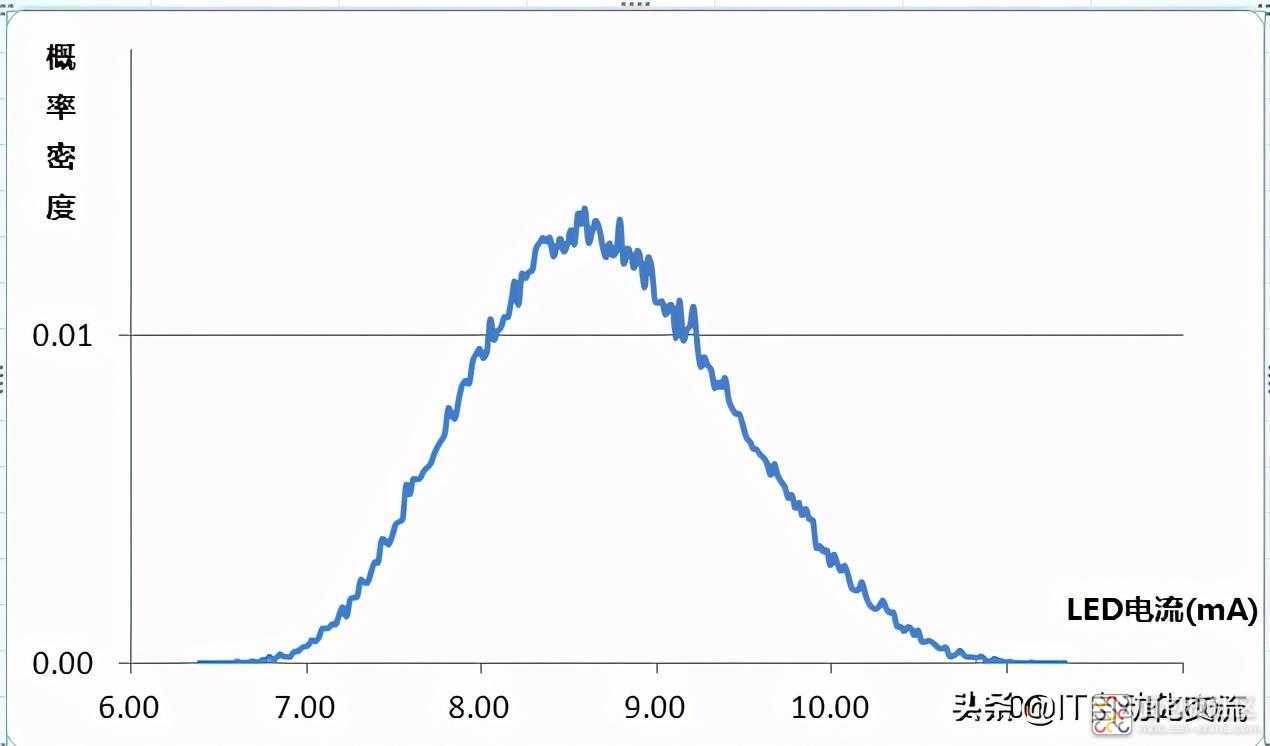
LED电流的概率密度曲线
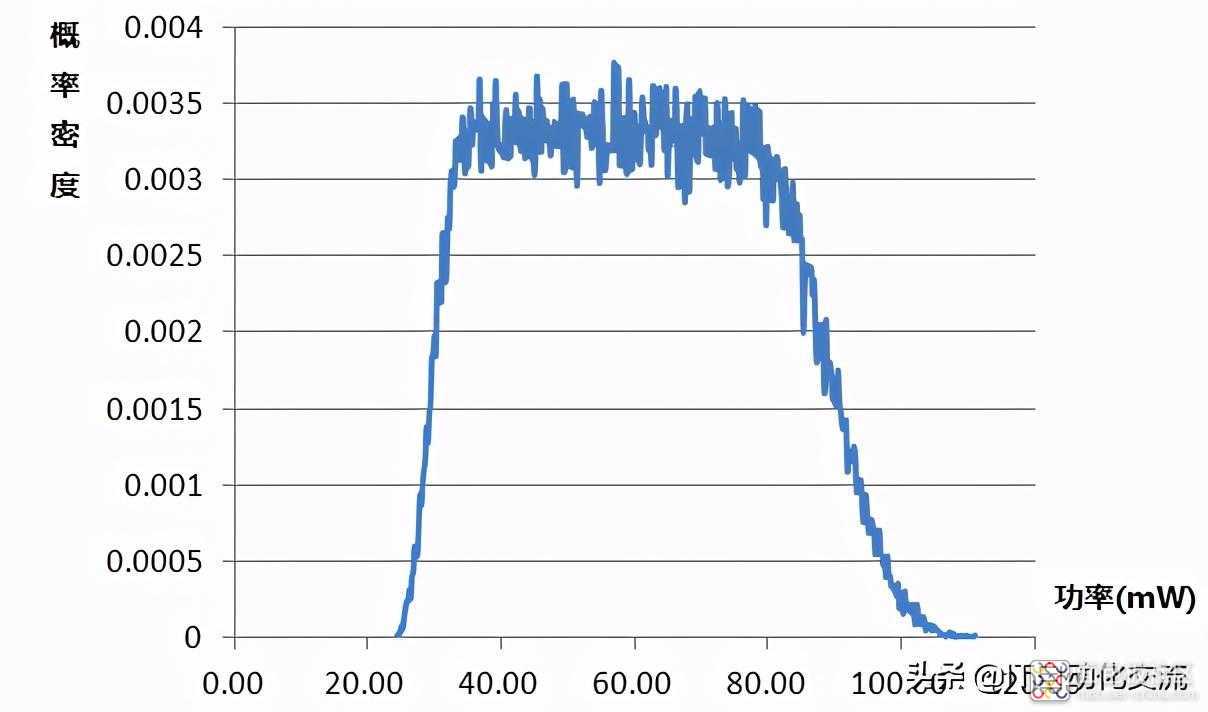
三极管功率的概率密度曲线
从数值结果来看,
LED的平均电流为:8.70mA,标准差σ为0.73mA;
取+/-3σ为最小、最大值,得到最小电流为:6.51mA,最大电流为:10.89mA;
波动范围比较小。
三极管功耗的平均值为:60.1mW,标准差σ为18.2mW,
取+/-3σ为最小、最大值,得到最小功率为:5.2mW,最大功率为:115mW。
在其允许最大功耗200mW范围内,所以在最坏情况下,三极管的功耗仍能满足规格要求;
来源:物联网全栈开发






 /4
/4 

