我们知道,OFDM技术的推出其实是为了提高载波的频谱利用率,或者是为了改进对多载波的调制,它的特点是各子载波相互正交,使扩频调制后的频谱可以相互重叠,从而减小了子载波间的相互干扰。
在对每个载波完成调制以后,为了增加数据的吞吐量、提高数据传输的速度,它又采用了一种叫作HomePlug的处理技术,来对所有将要被发送数据信号位的载波进行合并处理,把众多的单个信号合并成一个独立的传输信号进行发送。另外OFDM之所以备受关注,其中一条重要的原因是它可以利用离散傅立叶反变换/离散傅立叶变换(IDFT/DFT)代替多载波调制和解调。
OFDM的基本原理是将高速信息数据编码后分配到并行的N个相互正交的载波上,每个载波上的调制速率很低(1/N),调制符号的持续间隔远大于信道的时间扩散,从而能够在具有较大失真和突发性脉冲干扰环境下对传输的数字信号提供有效地保护。OFDM对多径时延扩散不敏感,若信号占用带宽大于信道相干带宽,则多径效应使信号的某些频率分量增强,某些频率分量减弱(频率选择性衰落)。
OFDM的基本原理是将高速信息数据编码后分配到并行的N个相互正交的载波上,每个载波上的调制速率很低(1/N),调制符号的持续间隔远大于信道的时间扩散,从而能够在具有较大失真和突发性脉冲干扰环境下对传输的数字信号提供有效地保护。OFDM对多径时延扩散不敏感,若信号占用带宽大于信道相干带宽,则多径效应使信号的某些频率分量增强,某些频率分量减弱(频率选择性衰落)。
OFDM的频域编码和交织在分散并行的数据之间建立了联系。这样,由部分衰落或干扰而遭到破坏的数据,可以通过频率分量增强部分的接收的数据得以恢复,即实现频率分集。
OFDM增强了抗频率选择性衰落和抗窄带干扰的能力。
OFDM增强了抗频率选择性衰落和抗窄带干扰的能力。
在单载波系统中,单个衰落或者干扰可能导致整个链路不可用,但在多载波的OFDM系统中,只会有一小部分载波受影响。此外,纠错码的使用还可以帮助其恢复一些载波上的信息。通过合理地挑选子载波位置,可以使OFDM的频谱波形保持平坦,同时保证了各载波之间的正交。
时域上的波形分析
OFDM的"O"代表着"正交",那么就先说说正交吧。
首先说说最简单的情况,sin(t)和sin(2t)是正交的。
如下证明sin(t)·sin(2t)在区间[0,2π]上的积分
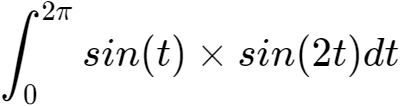
为0,
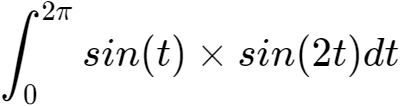
根据积化和差公式,
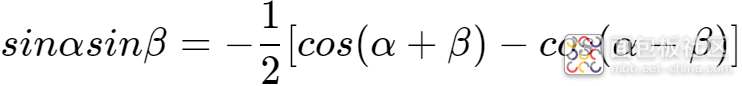
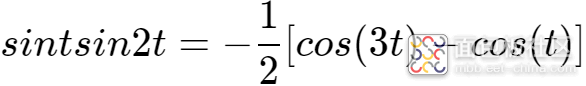
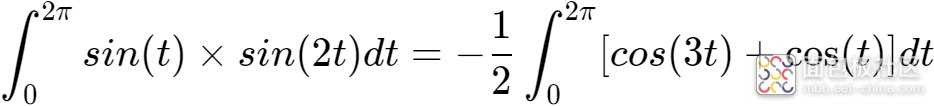
根据三角函数积分公式,
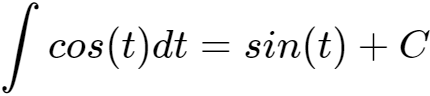
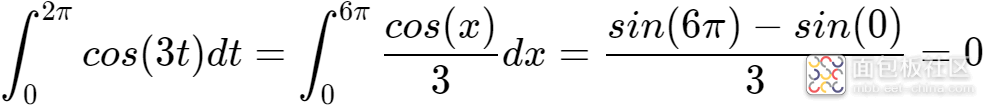
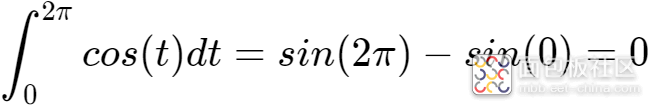
所以:
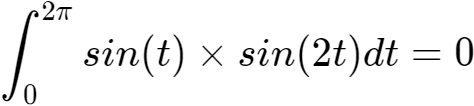
用图形的方式理解正交性,
在下面的图示中,在[0,2π]的时长内,采用最易懂的幅度调制方式传送信号:
sin(t)传送信号a,因此发送a·sin(t),
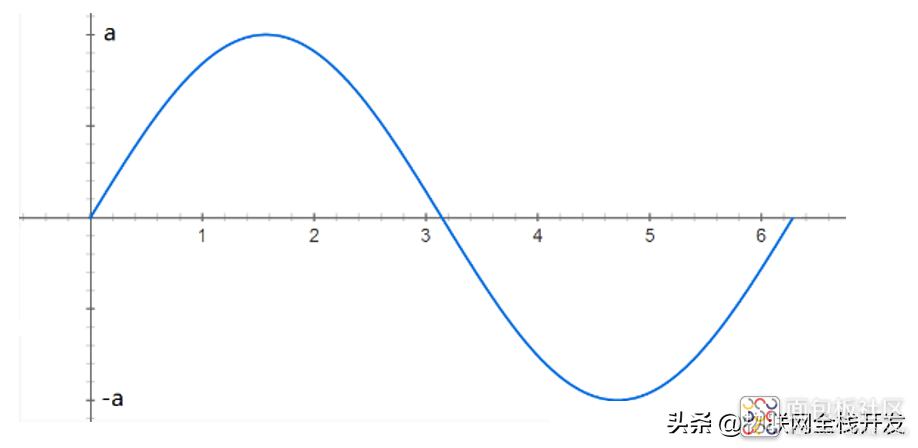
发送a信号的sin(t)
sin(2t)传送信号b,因此发送b·sin(2t)。
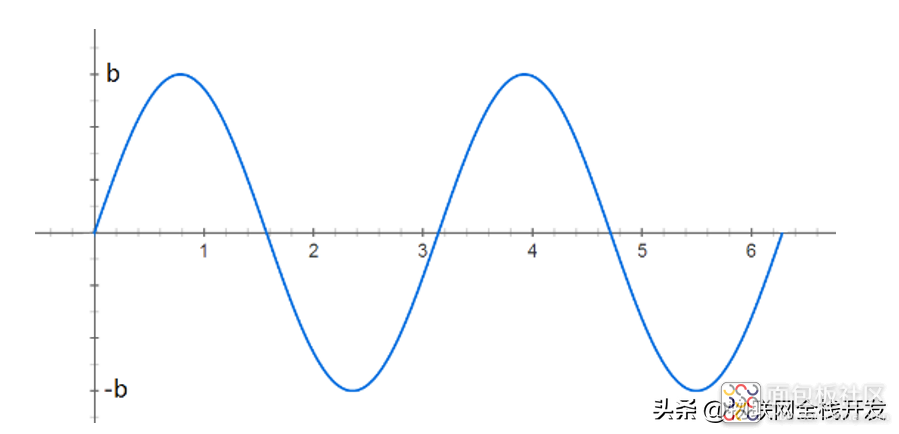
发送b信号的sin(2t)
其中,sin(t)和sin(2t)的用处是用来承载信号,是收发端预先规定好的信息,在本文中一律称为子载波;
调制在子载波上的幅度信号a和b,才是需要发送的信息。
因此在信道中传送的信号为a·sin(t)+b·sin(2t)。
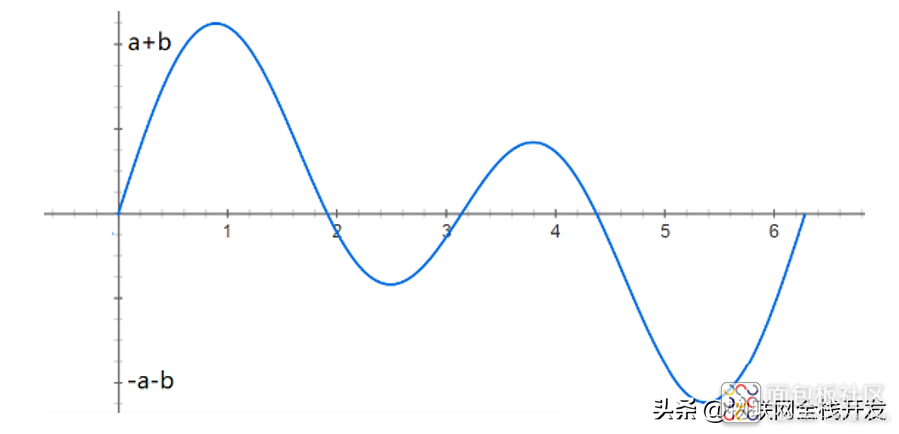
在信道中传送的叠加信号a·sin(t)+b·sin(2t)
在接收端,分别对接收到的信号分别乘以sin(t)和sin(2t)并在[0,2π]的时长内积分,就可以得到a和b了。
假设f(t)=a·sin(t)+b·sin(2t),
f(t)·sin(t)=[a·sin(t)+b·sin(2t)]·sin(t)的波形如下:
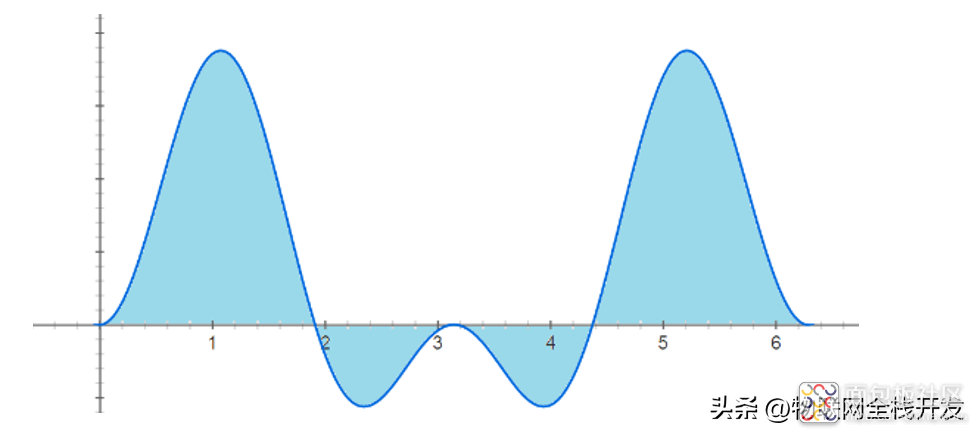
[a·sin(t)+b·sin(2t)]·sin(t)的波形
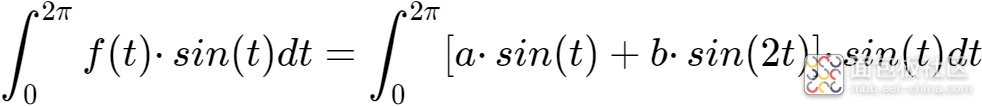
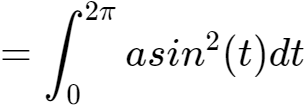
根据二倍角公式,
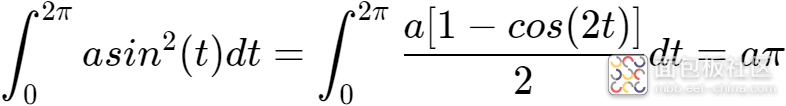
f(t)·sin(t)=[a·sin(t)+b·sin(2t)]·sin(2t)的波形如下:
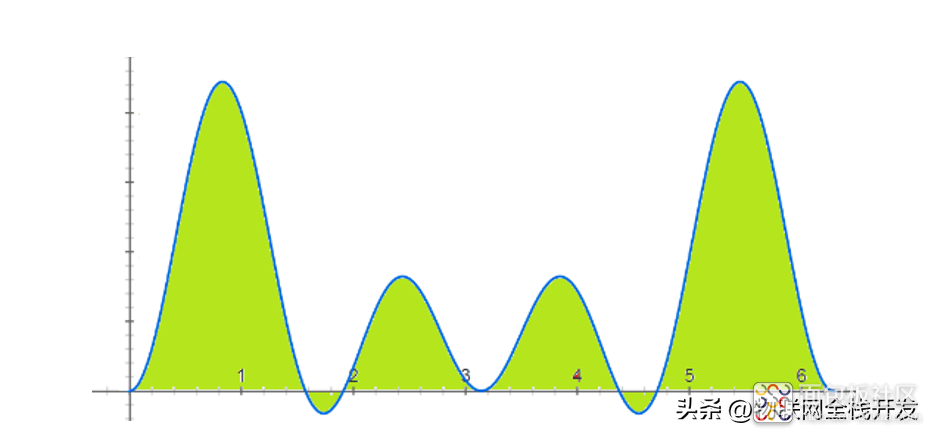
[a·sin(t)+b·sin(2t)]·sin(2t)的波形
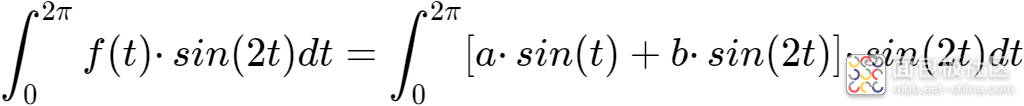
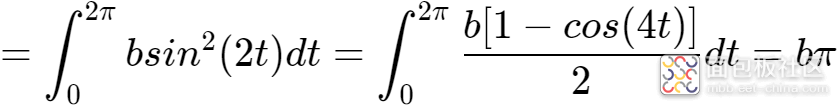
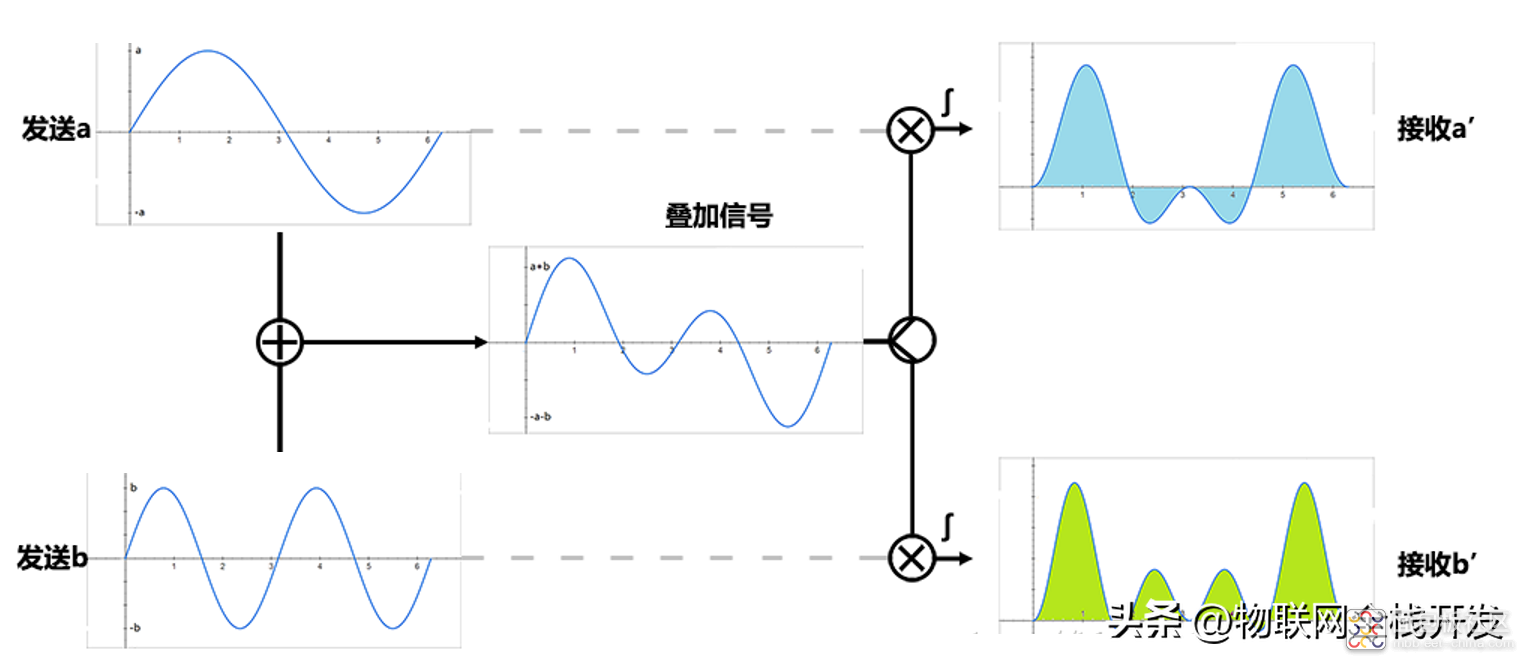
发送和接收的流程框图
上面的图示虽然简单,但是却是所有复杂的基础。
1.1 下一步,将sin(t)和sin(2t)扩展到更多的子载波序列{sin(2π·Δf·t),sin(2π·Δf·2t),sin(2π·Δf·3t),...,sin(2π·Δf·kt)} (其中k=16,256,1024等),应该是很好理解的事情。其中,2π是常量;Δf是事先选好的载频间隔,也是常量。1t,2t,3t,...,kt保证了正弦波序列的正交性。
1.2 再下一步,将cos(t)也引入。
容易证明,cos(t)与sin(t)是正交的,也与整个sin(kt)的正交族相正交。
同样,cos(kt)也与整个sin(kt)的正交族相正交。
因此发射序列扩展到{sin(2π·Δf·t),sin(2π·Δf·2t),sin(2π·Δf·3t),...,sin(2π·Δf·kt),cos(2π·Δf·t),cos(2π·Δf·2t),cos(2π·Δf·3t),...,cos(2π·Δf·kt)}也就顺理成章了。
1.3 经过前两步的扩充,选好了2组正交序列sin(kt)和cos(kt),这只是传输的"介质"。
真正要传输的信息还需要调制在这些载波上,即sin(t),sin(2t),...,sin(kt)分别幅度调制a1,a2,...,ak信号,cos(t),cos(2t),...,cos(kt)分别幅度调制b1,b2,...,bk信号。
这2n组互相正交的信号同时发送出去,在空间上会叠加出怎样的波形呢?做简单的加法如下:
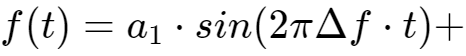
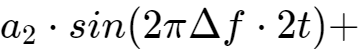
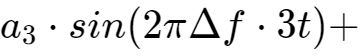
...
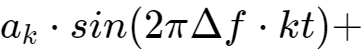
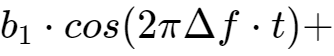
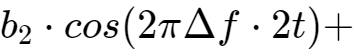
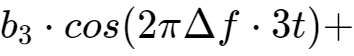
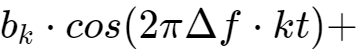
...
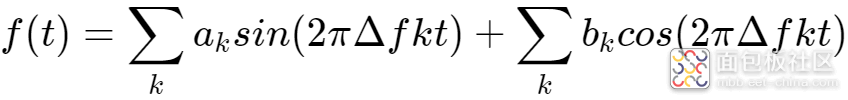
为了方便进行数学处理,上式有复数表达形式,如下:
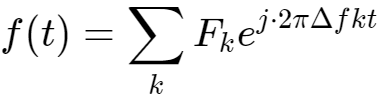
上面的公式可以这样看:
每个子载波序列都在发送自己的信号,互相交叠在空中,最终在接收端看到的信号就是f(t)。
接收端收到杂糅信号f(t)后,在每个子载波上分别作相乘后积分的操作,就可以取出每个子载波分别承载的信号了。
上面1.1-1.3的扩展,可如下图所示:
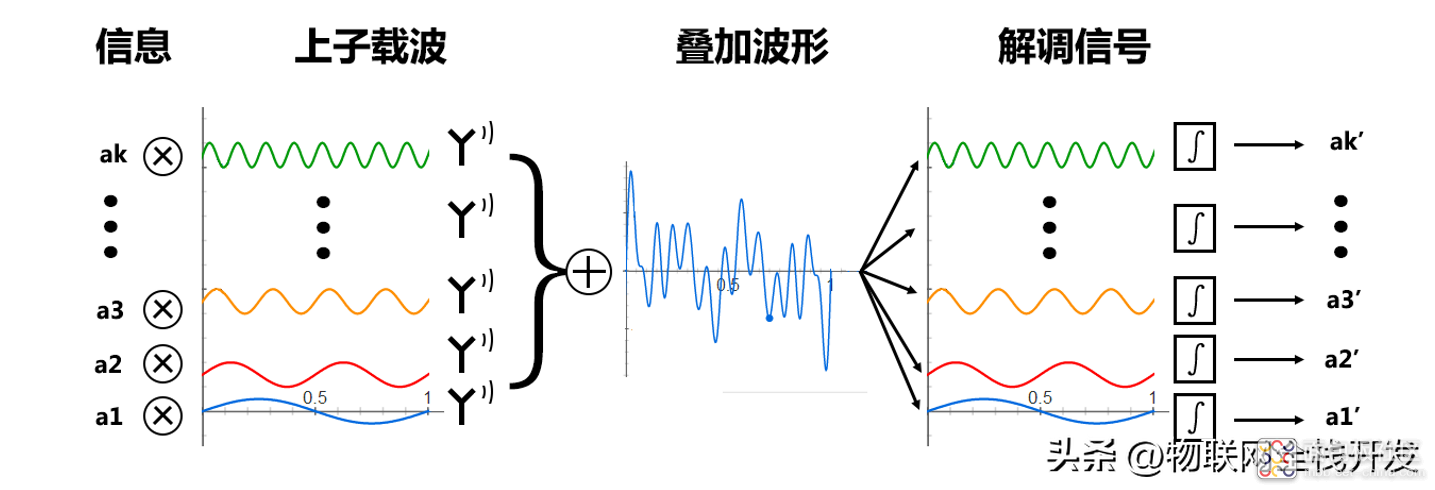
时域上的OFDM系统图
LTE子载波的间隔Δf=15kHz,一个OFDM symbol的发送时间是66.7us,可以发现,15kHz*66.67us=1,即基带上一个OFDM symbol的发送时间正好发送一个一次谐波的完整波形。
对于10M的LTE系统,采用的是1024个子载波,但是只有中间600个(不含最中间的直流)子载波被用于传送数据。
在一个OFDM symbol的时间内(即66.67us),靠近中间的两个一次谐波传输一个完整波形,再靠外一点的两个二次谐波传输两个完整波形,以此类推至最外面的两个300次谐波传输了300个完整的波形。
在这66.67us内,600个子载波互相正交,其上分别承载了600个复数信号。






 /3
/3 
