通过数据采集系统采样得到的振动信号数据往往叠加有不规则的随机干扰信号。由于随机干扰信号的频带较宽,有时高频成分所占比例还很大,是的采集到的数据绘成的振动曲线上呈现许多毛刺,为了消除干扰信号的影响,提高振动曲线的光滑度,常常需要对采样数据进行平滑处理。利用最小二乘法原理对离散数据进行线性平滑的方法称为直线滑动平均法。
MATLAB源程序如下:
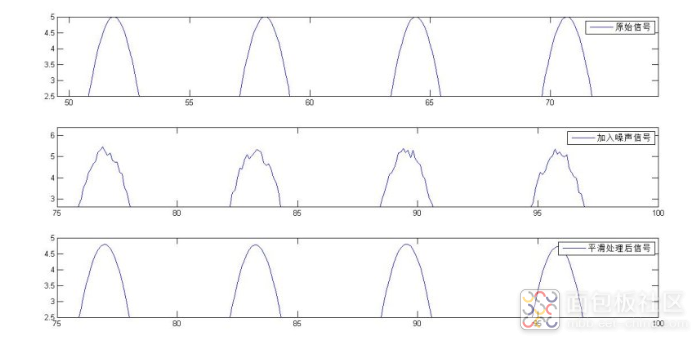
function y = mean5( x,n )%五点滑动平均分法平滑处理 % 输入 % x 待平滑信号 % n 平滑次数 % 输出 % y 平滑后信号 %exanple: % N = 1000; % t=0:0.1:(N-1)*0.1; % x = 5*sin(t); % a = rand(1,1000)*0.5; % y = x+a; % subplot(311) % plot(t,x); % legend('原始信号') % subplot(312) % plot(t,y) % legend('加入噪声信号') % z = mean5(y,10); % subplot(313) % plot(t,z) % legend('平滑处理后信号') L = length(x);%信号长度 a = x; for k = 1:n b(1) = (3*a(1)+2*a(2)+a(3)-a(4))/5; b(2) = (4*a(1)+3*a(2)+2*a(3)+a(4))/10; for j = 3:L-2 b(j) = mean(a(j-2:j+2)); end b(L-1) = (a(L-3)+2*a(L-2)+3*a(L-1)+4*a(L))/10; b(L) = (-a(L-3)+a(L-2)+2*a(L-1)+3*a(L))/5; a = b; end y = a'; end
复制代码




 /5
/5 


