和其他时候一样,为了起草这篇文章,我使用了 3Blue1Brown 的一个公共视频,标题为“但是什么是卷积?” 只停在开头部分,因为我的目的是以尽可能简单的方式介绍这个主题。
数字和操作列表给定两个数字列表,可以通过多少种方式获得第三个列表?当然很多,或者无限,你会说。如果我们排列这两个列表,我们称它们为 “a” 和 “b”,在并排的两列中,我们得到一个表,其中的行数与每个列表中的数字一样多(前提是它们包含相同数量的项,但如果数量不同则没有任何变化,因为我们总是可以在缺失的部分添加零地方)。这是通常使用 Excel 完成的操作。然后可以在第三列中将同一行的两项相加,或者将它们相乘;例如“数量”和“单价”来计算您购买一系列“每公斤很多”的产品所花费的费用,就像在某种程度上具有分析性的购物清单中一样。跳进数学,这两个列表也可以从同一变量的两个函数中获得,离散的或连续的, f(x) 和 g(x)。
卷积
但是还有另一个稍微复杂的操作可以在两个列表上完成,这个操作被证明是非常重要的并且有一个有点吓人的名字“卷积”。它是一个与“进化”和“退化”一样的名称,源自“volgere”,转向,弯曲。
两个序列或两个函数之间的卷积用星号表示:
a*b, f(x)*g(x) 或 [f*g](x) ,
这可能与简单的乘法相混淆,实际上我最初使用的是 x。
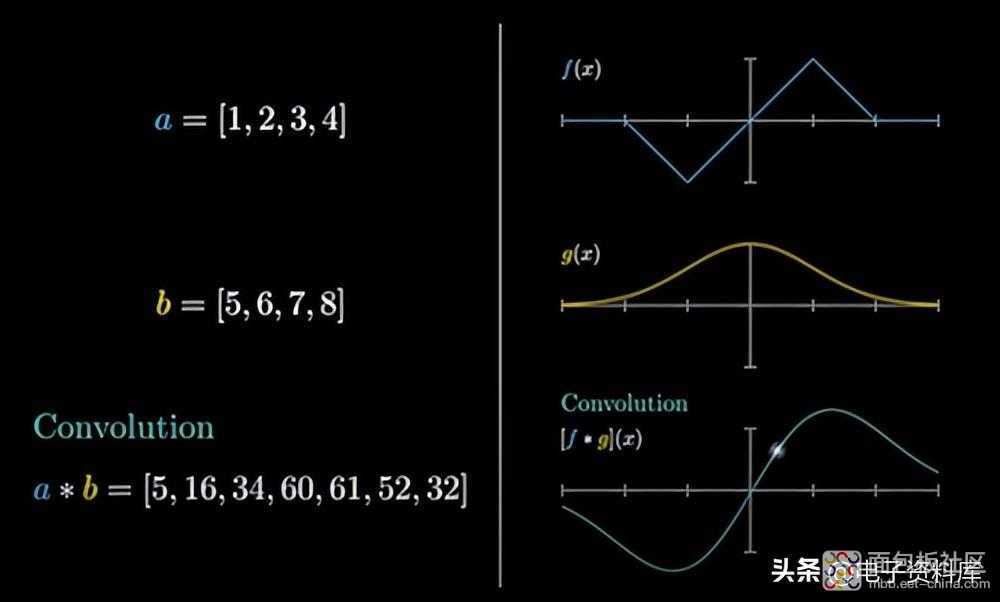
卷积 在人类活动或技术的各个领域都有应用 ,例如电气工程和电信,它在其中非常普遍,但也可能是隐藏的或没有意识到的。它没有 加法或 乘法那么直接,因为它是 两者的特定组合,无论如何 是线性组合。一般来说,当可以应用它时,线性是基本的,因为它保持比例,从而大大简化了生活)。
从现在开始,我们将使用术语“序列”代替“列表”,以更具体地表示我们指的是 数字列表。
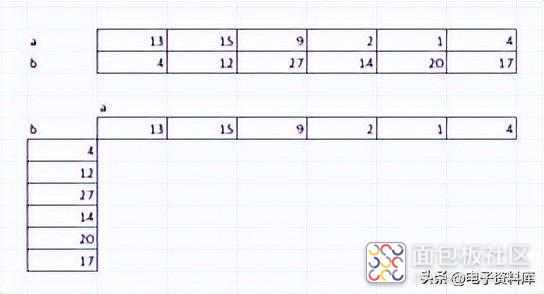
为了获得两个序列a 和 b之间的卷积, 将它们排列在 两条线 (而不是两列)或 两条垂直线上会在视觉上更具表现力 ,这会产生 类似于“乘法表”的表格,那些学到的在小学能够做乘法。
骰子
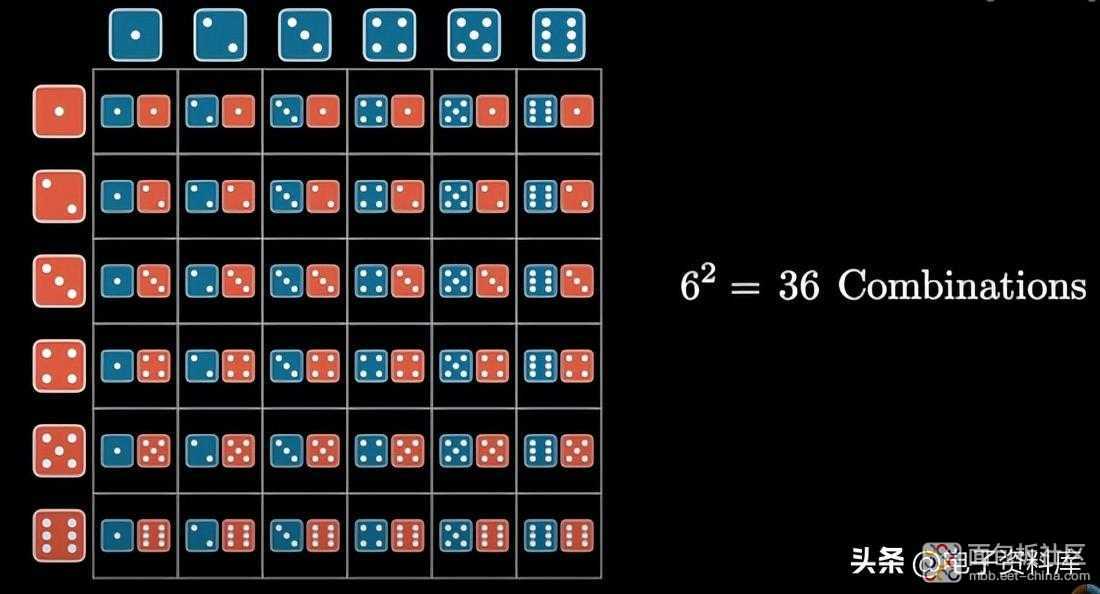
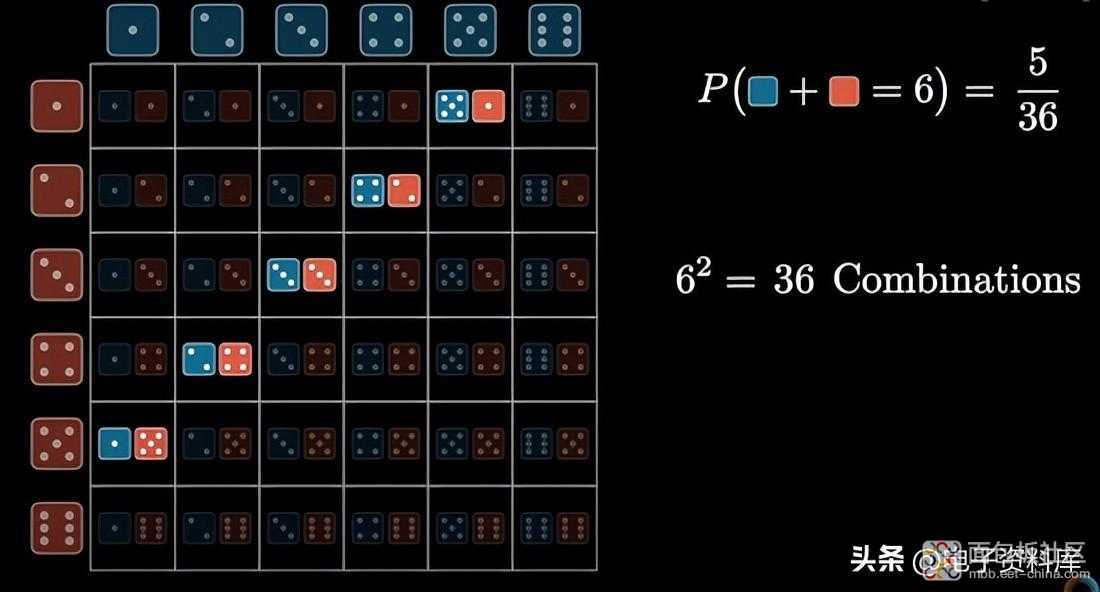
让我们从一个熟悉的实验开始:反复掷两个骰子。

有 36 种可能的结果,即“产品集”。假设我们想知道从抛掷中获得总和 S的概率。一次抛掷可以通过多少种方式获得这个总和?例如 S = 4 获得 2+ 2 or with 3 + 1 or with 1 + 3.出现任何骰子组合的概率(这里使用的术语“组合”是一般意义上的)是两侧概率的乘积,即 1 / 6x1/6 = 1/36;在这种情况下,有 3 种 组合给出 S=4,它的概率是 1/6x1/6 + 1/6x1/6 + 1/6x1/6 = 3/36。

4TAB
从图中我们可以看出和 S的每个给定值如何 驻留在 表的对角线上。
如果我们现在继续将 两个序列排列在两条线上, 我们就会意识到, 通过将第二个序列相对于第一个序列从左向右水平平移以便在每个位置连续叠加框,可以获得相同的结果步骤:第一个,然后两个,等等,直到完全重叠(对应于最大组合数)并继续直到没有重叠。在每个步骤中,执行相应的产品及其总和。
从下图可以推导出,这个过程正好对应于一个接一个地“展开”表格的对角线,然后添加项。
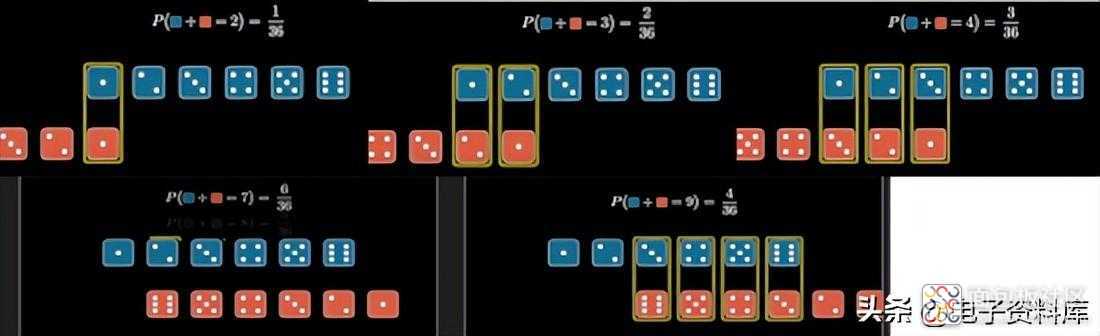
关于概率,我们假设 骰子的面 是 等概率的,即每一面都有 1/6 的概率出现。让我们考虑两个 已加载的骰子, A 和 B,其中 与 6 个 面 相关的概率都不同于1/6 ,我们称它们 为骰子 A 和 b 1的a 1, a 2,... a 6, b 2 , …, b 6坚果B 的那些 。现在 S=4 的 3 种组合 各有不同的概率,所以 S=4的概率 是 a 1 xb3 + a 2 xb 2 + a 3 xb 1。
该图显示了和 S的每个值的概率的所有组合 ,从 2 到 12。
得到的值序列各自作为乘积a i xb j 的和, 其中i+j 为常数,称为卷积a i * b j 。
由此可见, 当一个指数增加时,另一个指数下降,如图所示。

因此,仅使用 图中的索引i很方便,设置j=ni 并因此设置a i 和 b [ni],其中“ n ”是与每个步骤相关的总和,此处在2 和 12之间变化。例如,当 n=6时, i从1 变化 到 5,如图中 P(A+B=6)突出显示的情况所示。
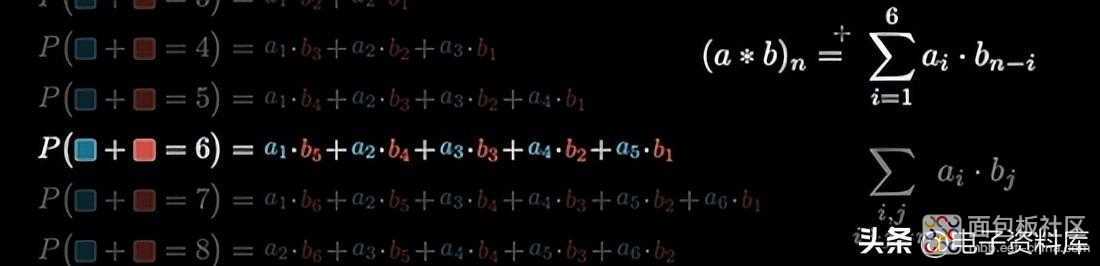
卷积采用索引 i的求和形式, 该索引会变化以覆盖除0 以外的所有项;在这个例子中,我的范围从 1 到 n-1。事实上,上图显示了11个 步骤,每个步骤代表了掷出的一对骰子具有该步骤对应的总和的概率。
需要强调的一点恰恰是 指数的倒置,在某种意义上,当 a 增加时, b 减少。为什么要强调呢?因为它通常会混淆。当我们将卷积应用于连续函数时(下一篇文章),有必要反转 两个函数之一的自变量的符号,这转化为“反转它”,以便第一个值成为最后一个值,第二个倒数第二个等等 卷积在德语中被称为Faltung并非巧合 ,意思是折叠,正如我们在上面所说的,由于意大利名称的起源。
在上面的离散概率图中也可以看到这种逆转;例如考虑 图中的P(A+B=6) ,为了形成单个加数,建议反转序列 b 1 -b 5 以便在 a a 1、 b 4 ad a 2 下找到 元素b 5等等。

除了操作程序之外,我们可以说,放弃数学严谨性,与两个独立事件(这里是两个骰子的掷骰)之和相关的概率分布是两个事件中每个事件的 概率分布的卷积。
其他继承现在让我们离开概率的上下文,考虑 两个数字序列的 一般卷积,即A = (1,2,3)和 B = (4,5,6)

该图仅显示了5 个滚动步骤中的两个 ,即第二个和最后一个。正如您所看到的,第二个序列被反转以按照正确的顺序执行操作,使用第二个序列相对于第一个序列的滑动。
为什么在面数相等的骰子示例中,第二个序列没有反转?因为作者狡猾地找到了一个索引与事件重合的例子,可以这么说。然而,一旦他介绍了加载的骰子,他就不再代表序列的翻译,而是简单地将对角线“拉直”,将桌子旋转 45 ° , 每条对角线获得一条线。
现在让我们考虑 两个多项式的乘积,其系数由上述两个序列表示,按幂递增排序:它只不过是一个等于多项式卷积的多项式。

即使多项式按降序排序,这也能很好地工作,您可以很容易地验证这一点。
当然,它适用于 两个数字之间的普通乘法:
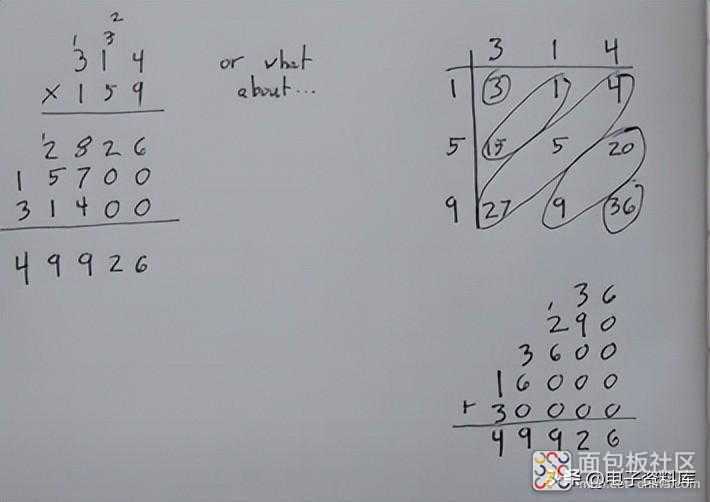
当我们“手动”执行乘法时,实际上我们执行的是卷积运算,我们不是将第二个数字(第二个序列)移动,而是将其结果向左移动。这里显示的是两个3 位数 之间的乘法 ,它产生一个方表,但当然它也适用于不同位数的数字。
总而言之,我们可以说 卷积是一种线性运算,即在水平叠加的两个数字序列(两条线)之间进行的特定线性组合 ,其中第二个序列在倒置之后,即各项已放在相反的顺序(最后一个变成第一个,倒数第二个变成第二个,等等),它从左向右流动,而第一个保持静止。对于每个滑动步骤, 都会发生两个连续的操作:上面每对项的乘积和 这些乘积的总和, 其结果是 一个新序列的一项,它恰好是前两个的卷积。
正如我们在前面的例子中看到的,序列也可以是 多项式的一组系数。在两个序列重合的特定情况下,卷积对应于 多项式的平方。然后,如果我们想对多项式进行立方,则在由此获得的平方多项式与多项式的一次幂之间执行卷积就足够了。可以针对更高的功率重复该过程。那么,在二项式的情况下,可以看到卷积和 Tartaglia 三角形之间的关系。
最终 两个序列的卷积是 第三个序列,其中的每一项由以下公式得到:

定义

在第二个公式中,可以清楚地看到两个序列如何也可以具有不同数量的项,正如已经针对“手动”执行的乘法所说的那样。
同样出于同样的原因,可以推导出卷积是可交换的,也就是说,对于上面的例子,它是 y(n) = h(n) * h(n) = h(n) * x(n)。
结论本文中所写的内容试图阐明一个概念,正如书中经常出现的那样,它并不完全直观,但它是一个具有相当广泛应用的概念。对此,我直接引用 维基百科 词条Convolution :
“卷积及其运算用于工程和数学的各种应用。
· 在统计学中,加权移动平均是一种卷积。两个独立随机变量之和的概率分布也对应于它们每个分布的卷积。
· 在光学中,许多种“模糊”都是用卷积来描述的。阴影(例如当物体放在光源前面时可以看到的桌子上的阴影)是光源形状的卷积,它投射出被照物体的影子和物体本身。散焦照片是对焦图像与光圈形状的卷积。这种效果的摄影术语是散景。
· 同样,在数字图像处理中,卷积滤波器在计算边缘和相关过程的算法中起着重要作用。
在数字信号处理中,频率滤波可以通过将两个函数(带滤波器的数据)在时域进行卷积来简化,相当于将数据乘以频域滤波器。
· 在线性声学中,回声是原始声音与描述反射声音信号的各种对象的几何函数的卷积。
· 在数字信号处理中,人工混响卷积用于将真实房间的脉冲响应编码为数字音频信号。
在电气工程和其他学科中,线性(静止)动态系统的输出(响应)是输入(输入激励)与系统脉冲响应的卷积(即,激励 d 输入时的响应是 Dirac Delta功能)。在离散域中,卷积的概念被扩展为求和,扩展为信号与脉冲响应的乘积 [4],序列 h(n) 被称为“卷积核”或“卷积掩码”。
在时间确定的荧光光谱中,激发信号可以被视为一串 delta 脉冲,测得的荧光由每个 delta 脉冲的指数衰减之和给出。”






 /5
/5 


