傅里叶变换不但广泛应用于信号处理，声学，无线电，以及热力学，而且还广泛应用于图像分析，检测，图像过滤，以及图像压缩等。
但我们为什么要进行傅里叶变换，面对枯燥的数学公式，很少有人能深入的思考这个问题，本篇我们就用形象的图形来说明这一点，浅显易懂，容易理解
傅里叶级数可以把任意一个周期函数分解成无穷多个正弦或余弦波，傅里叶把三角函数的应用推向了一个难以想象的高度。
0f7583a948934b6aa47cbc85f2050a93~noop.image?_iz=58558&from=article.jpg

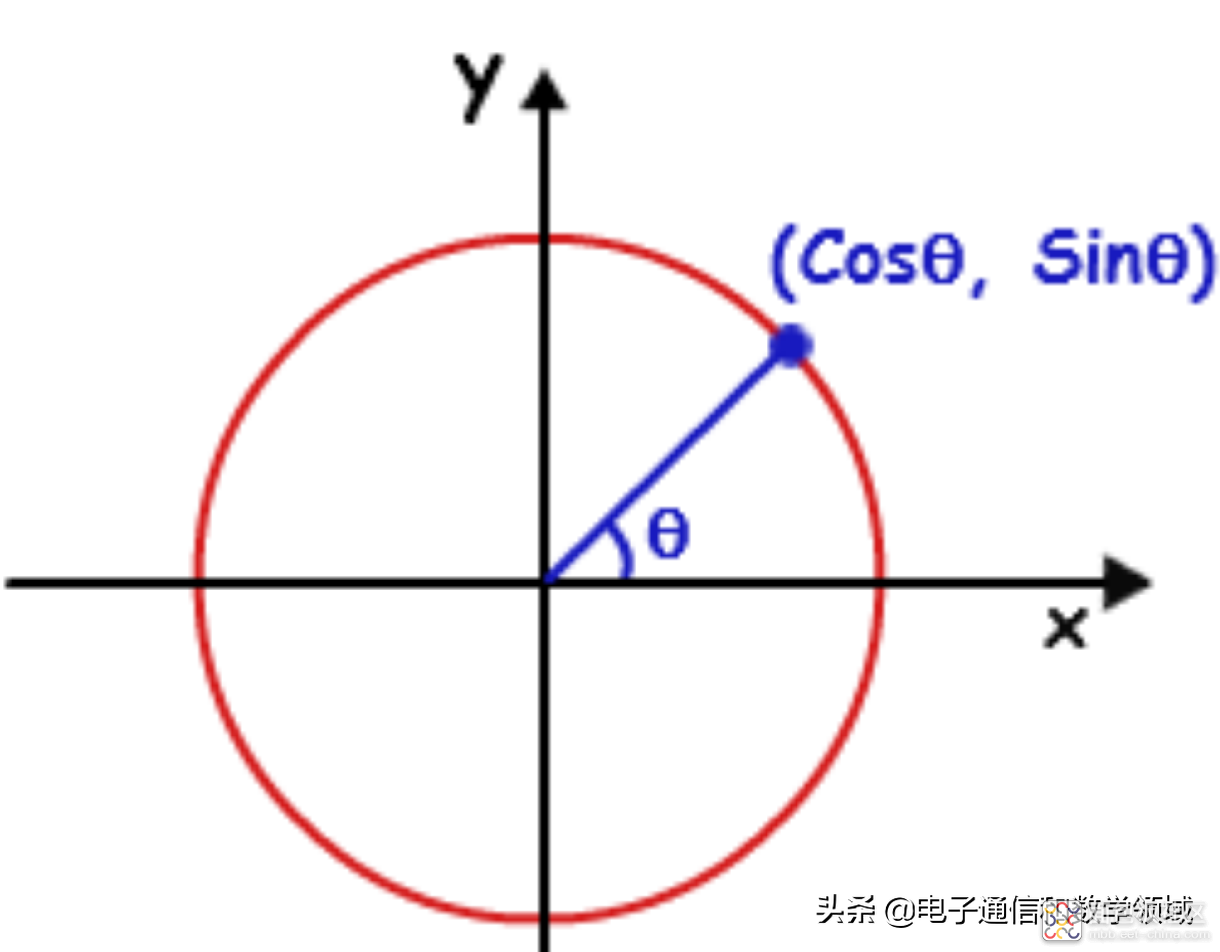
为了更加容易理解，从最熟悉的正弦和余弦波开始
62f14185d4394d66bf127559b4b4c1ea~noop.image?_iz=58558&from=article.jpg

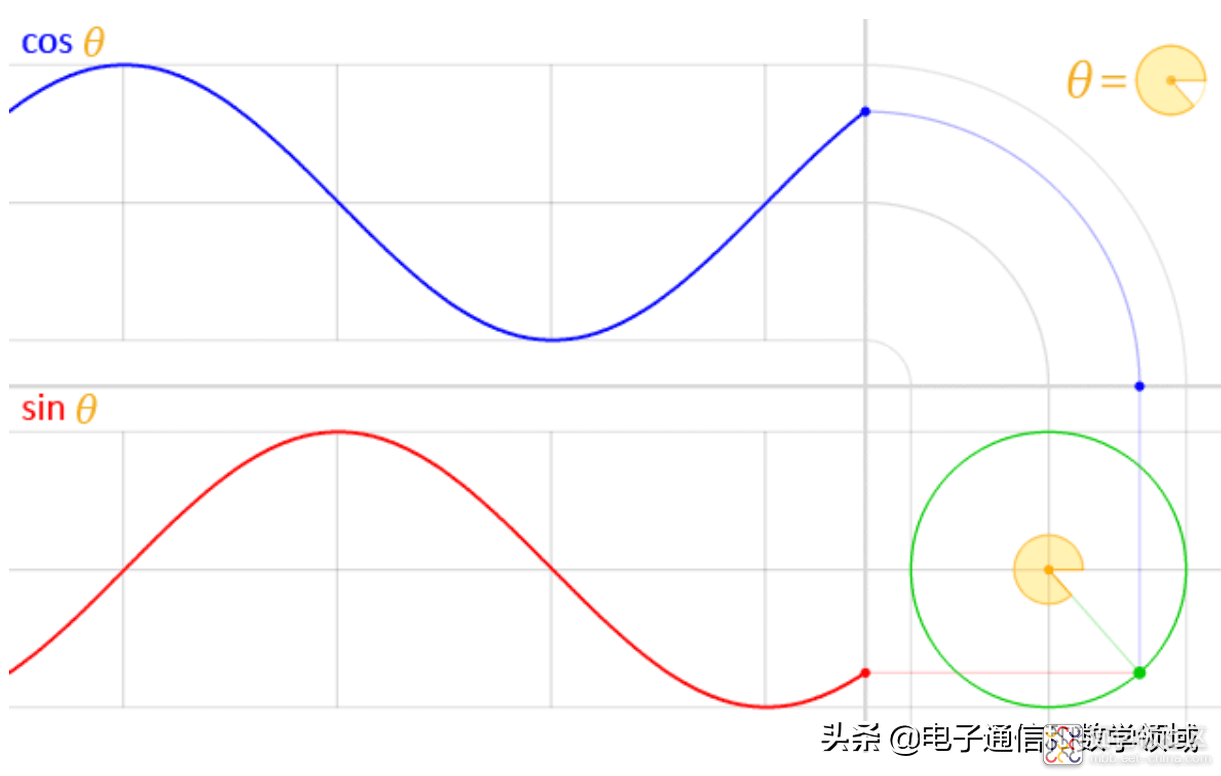
首先假设有一个信号，我们记作x(t)，如下图
6f2404512ef74fb6bef236be80382de5~noop.image?_iz=58558&from=article.jpg

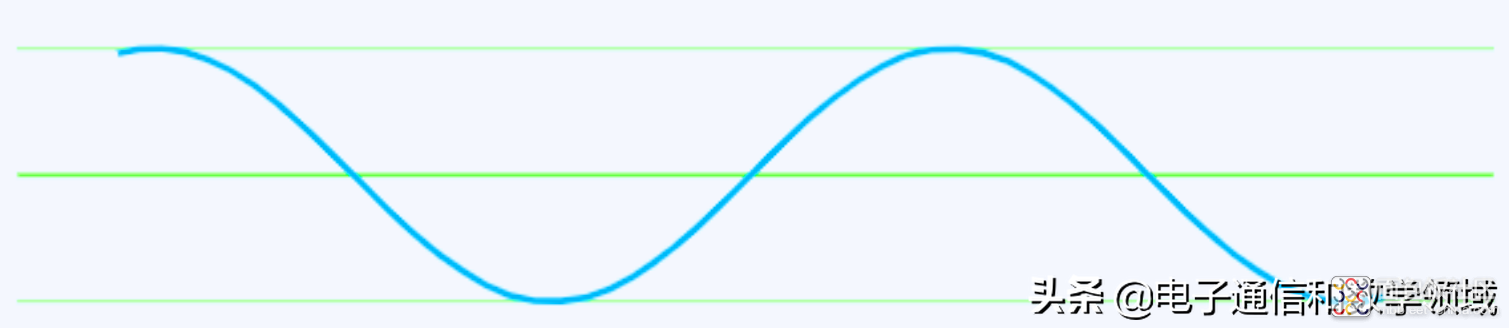
同一时间我们触发，另一个信号y(t)
b89d7597ca614be189d4aa93d84bc723~noop.image?_iz=58558&from=article.jpg

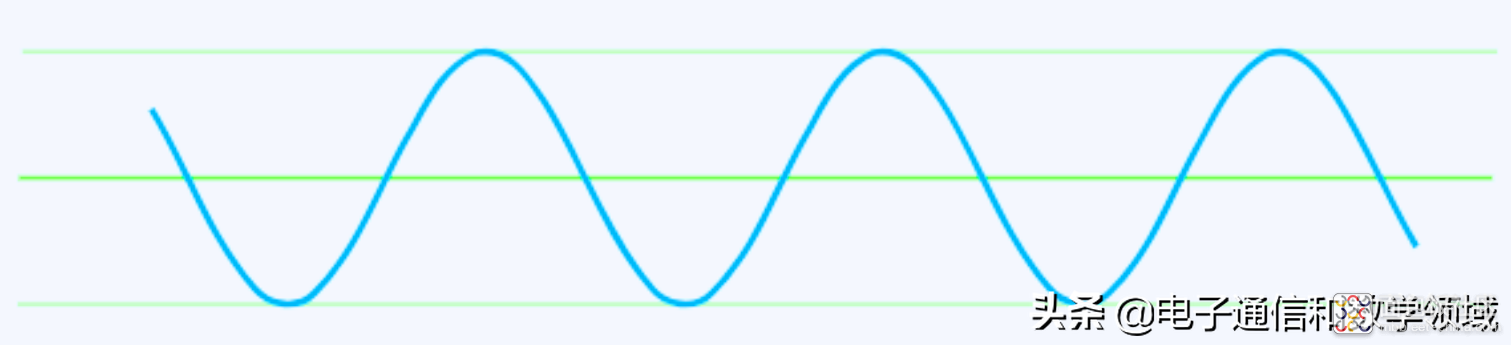
把这两个信号叠加在一起，我们就得到一个新的信号，这个新的信号的振幅，就是x(t)和y(t)两个信号振幅的叠加：即z(t)=x(t) + y(t)
803a34e3e5b748fa896ef4942d234f3c~noop.image?_iz=58558&from=article.jpg

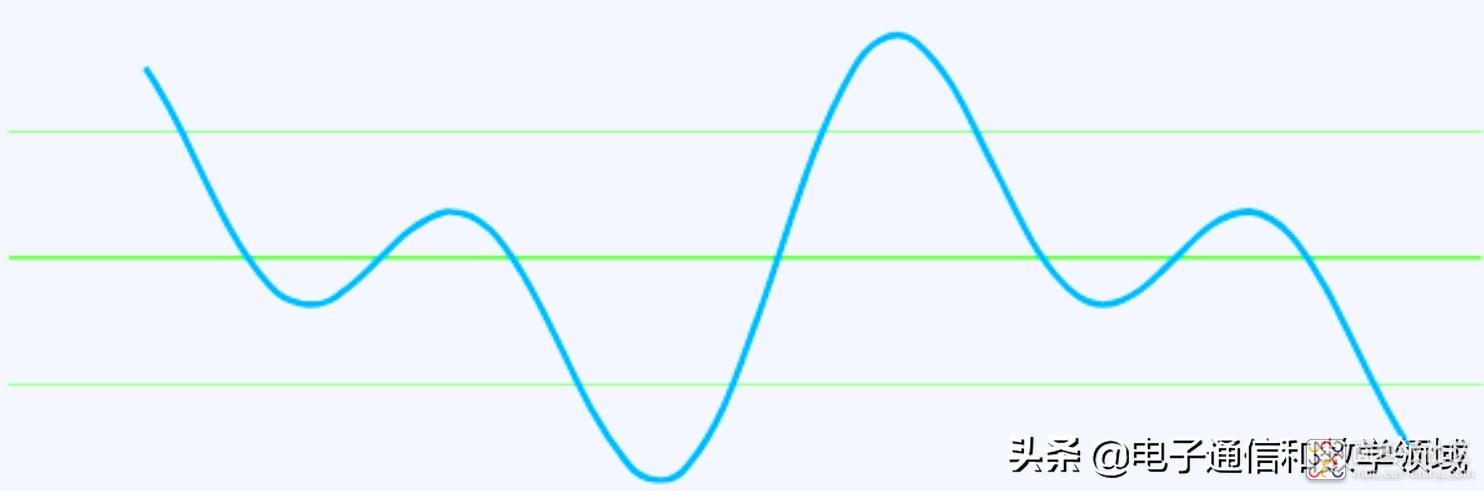
现在要思考的是：如果只有信号z(t)，你能分离出它的叠加信号x(t)和y(t)吗？
答案是肯定的，这就要用到傅里叶变换技术。它首先将信号z(t)分解成所有组成信号的频率
即：将原信号z(t)从时域转换到了频域，然后再从频域转移到时域
9cf29c955bf3494b85c424a6de1eac62~noop.image?_iz=58558&from=article.jpg

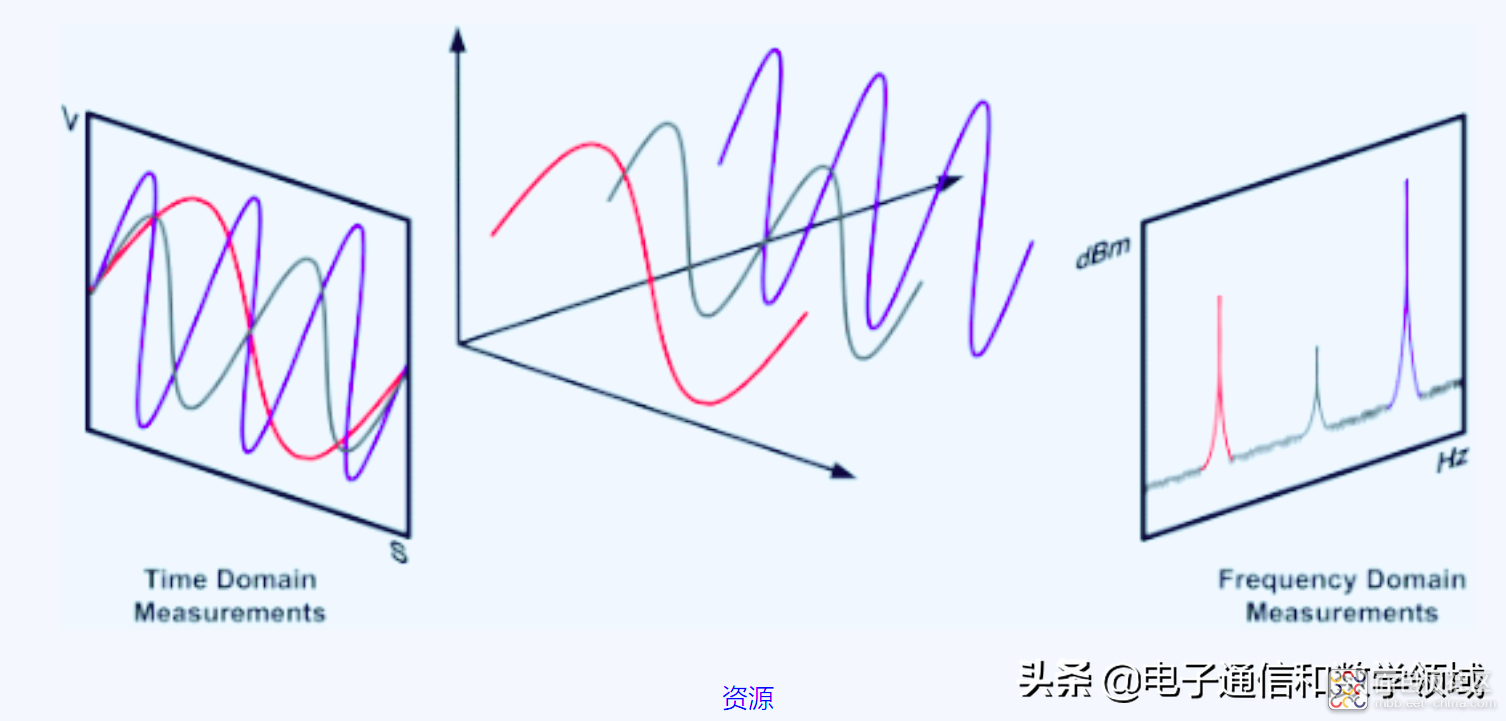
时域内的连续信号都可以用正弦信号的无穷级数形式表示出来
7a9aedd3b76c4daaaa75e7fdce802576~noop.image?_iz=58558&from=article.jpg

要从频域转换到时域，我们就要使用傅里叶反变换(IFT)

来源：电子通信和数学领域