数字控制系统是以微型计算机作为控制器,通过软件的方式来实现控制规律的一种控制系统。当我们想要改变控制器的控制规律,一般只要通过改变相应的程序或者软件参数即可以实现改变控制规律。
数字控制系统的示意图如下:
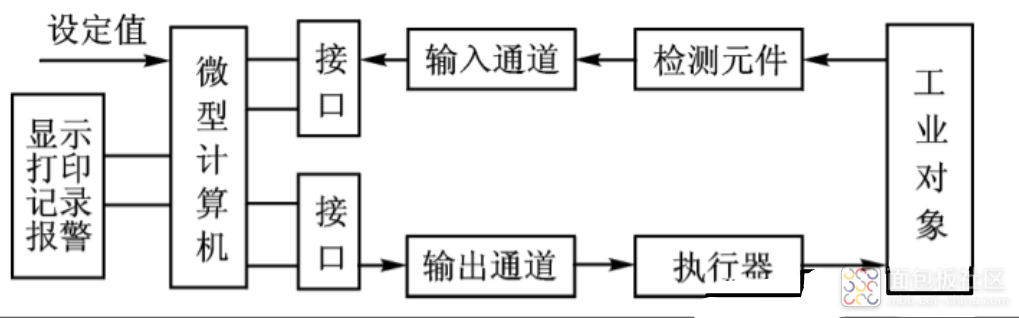
通过数字控制实现的PID的差分方程如下:

数字PID:指的是PID控制算法的实现是通过计算机软件程序实现的,计算机需要对输入的连续信号进行采集,然后通过量化作为控制器的输入参数,从而经过算法的调节实现目标对象的控制。
PID控制算法在计算机系统中,一般都是采用的数值逼近的方法进行的。因为在很多的系统中,它一般都是连续的,而计算机要进行运算就要依靠计算机的运算,计算机的运算是离散的。所以想要让计算机能够实现PID算法程序,就必须要将PID算法的连续函数进行离散化,从而能够在计算中通过软件算法的方式实现。
一般而言,计算机实现PID算法的时候,在采样周期很小的时候,积分部分可以用对误差求和的方式代替,微分部分可以用差商的方式代替,从而实现将连续的PID算法的差分方程进行离散化,能够通过计算机实现。
数字PID主要有两种:位置式PID和增量式PID
3.1、位置式PID
位置式PID:指的是PID控制器经过运算输出的Uk是被控对象的实际控制量大小。
这个概念是不是咋一看有点拗口?不理解?别急,举个例子看看就知道了。
打个比方:我要进行一个阀门的控制,从而控制流体的流量大小。假设阀门的开度位置为0~100,当前阀门的开度在位置20的地方。现在我希望加大流体的流量,通过修改设定值,PID通过调节,最终输出控制量Uk=80,即这个时候阀门的开度要到80的位置。这就是位置式PID输出的是对被控对象的实际控制量大小的理解。

再来位置式PID的离散公式。如下:
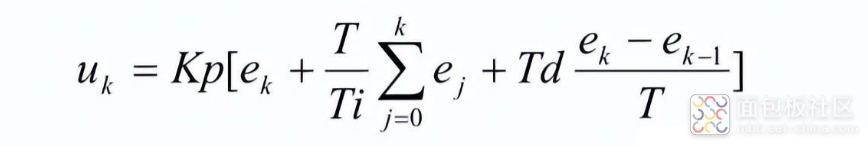
式中:

通过进一步整理,可以表示为:
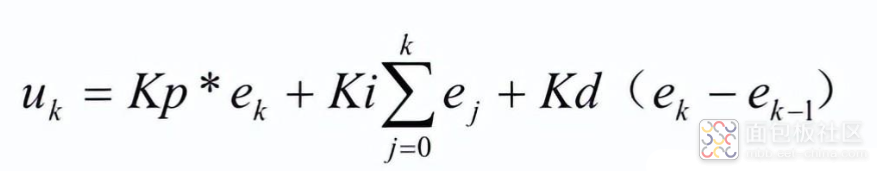
其中:
Kp - 比例系数Ki - 积分系数;Ki = Kp*T/Ti;Kd - 微分系数;Kd = Kp*Td/T;T:采样时间Ti:积分时间Td:微分时间
从上面的公式可以看出,位置式PID只需要计算第K次和K-1次的误差即可,并且控制器会对偏差进行累加,也就是控制器的每次输出Uk都和过去的状态有关。
这也会带来一些问题,因为位置pid的输出Uk和以前的状态有关,如果控制器出现异常,那么可能会导致Uk的输出大幅变化,导致执行机构的状态大幅变化,严重的话可能会导致严重的生产事故。
另外,因为位置PID要对偏差进行累积,所以会导致系统的运算量变大,这对于运算性能不够好的计算机也是一种负担。





 /5
/5 


