首先我想就二者的比较优势做一番评论——它们在您的工具箱里均有“一席之地”。下表可作为一个简便的参考:

价格、功耗这几个比较项目想必不需要再做澄清说明,但其余几项相对来说则不那么常见哦~
- 频率分辨率
- 频率捷变性
- 相位/幅度分辨率与捷变性
- 宽频谱纯度
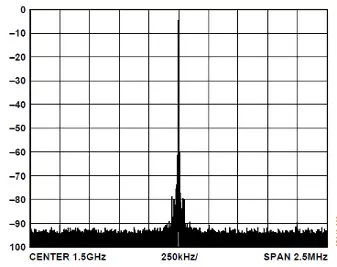
基于PLL的设计示例(摘自AD9510数据手册)
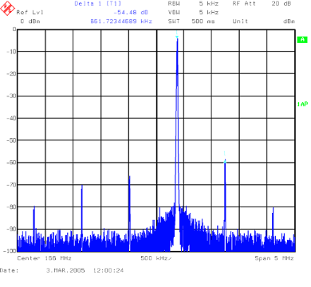
基于DDS的设计示例(在实验室利用AD9911测得的数据)
- 频率上变频
公平地说,并没有什么固定规则,这张表中几乎每一行都有一些微妙之处。
DDS与PLL的细微差别
这里先谈谈我认为更适合DDS的一些特点。
- 频率分辨率
有一款DDS运行速度为400 MSPS,使用48位调谐字(AD9956),由此得到的调谐分辨率不低于1.42 µHz,不错,其单位是微赫兹。标准PLL的分辨率受限于环路中分频器的深度,比这要差几个数量级。但有一点必须要提,小数 N分频 PLL(N为PLL中反馈分频器的分频系数)能够显著缩小该差距。但使用小数N分频PLL有弊端:输出中杂散会更多,信号抖动更厉害。
还要注意的一点是,标准DDS无法达到许多精确比率。在标准DDS频率公式中,分母总是2的幂。例如,若采样时钟为200 MHz,您可以精确地获得50 MHz频率(/4),但不能精确地获得40 MHz频率——会有一点偏差:如果使用的是AD9956,那么结果要么是比 40 MHz 少 0.142uHz,要么是比 40 MHz 多 0.568uHz。
标准PLL可以相当轻松地实现这些精密比率。因此,如果您需要精确的比率,应避免使用标准DDS。但是,这并不意味着您需要全然规避DDS,其实DDS也有其优势,比如可编程模数!
可编程模数DDS(我亲切地称之为 P-MOD)是DDS领域一项相对较近的创新。P-MOD DDS允许您改变DDS公式,使分母不再局限于2的幂。任何PLL在频率分辨率上都不及P-MOD DDS(如AD9913、AD9914、AD9915、AD9164)。我认为这是它的固有特性。我想我会在未来撰写更多有关P-MOD的博客,敬请期待~
回到上面的40 MHz例子,勤奋的工程师可能会设计一个采用跳频的系统,80%的时间位于比40 MHz低一点的频率,20%的时间位于比40 MHz高一点的频率,这样不仅能得到一个平均频率为40 MHz的信号,而且模仿了P-MOD的内部工作机制。
- 频率捷变性
跳频可利用两个并行PLL和一个开关实现(称为乒乓式PLL——无需桌子、球拍或网),但要么您需要为每个可能希望调到的频率使用一个完整PLL,要么您需要留出一定的建立时间以便改变旁路PLL的频率。
您也可以利用环路中的可变分频器扫频,但这样做的可控性或可重复性远不如DDS扫频。
- 相位分辨率与灵活性
- 幅度分辨率与灵活性
来源:本文由ADI时钟和信号部市场经理JLKeip撰写




 /4
/4 

