磁学基本定律
(1):均匀恒定磁场中,与磁场同方向的两点之间的磁动势为:
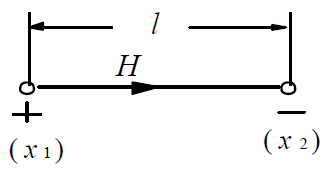
F = Hl
其中,H :为磁场强度;
l :为两点间的距离。
(2):均匀恒定磁场中,垂直穿过某一面积的总磁通为:
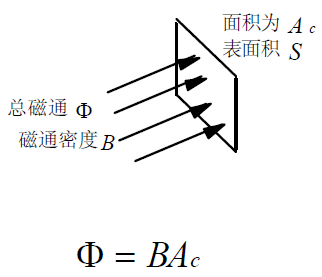
其中,B :为磁通强度;
Ac:包围所穿过磁通的面积。
(3):铁芯中的磁通密度与磁场强度之间的关系:
B = μH
其中,μ= μrμo:为铁芯材料的导磁率, μo 为真空的导磁率, μr 为铁芯材料的相对导磁率, μo = 4Π ×10-7 H /m,μr= 103 ~ 106
(4):法拉第电磁感应定律:

变化的磁通会在线圈中感应电压,大小满足上述公式,其中n 为线圈的匝数,方向由棱次定律判断。
(5):棱次定律:
由磁通感应的电压,企图产生一个电流,此电流产生的磁通将使穿过线圈的总磁通减小。具体是伸出左手,用拇指对准磁通的方向,则四指所指的方向即为感应电流的方向。
(6):安培定律:
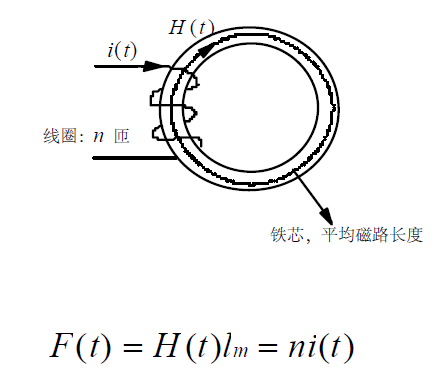
铁芯内的磁场是由外加线圈中的电流所产生的,其大小满足上述公式。
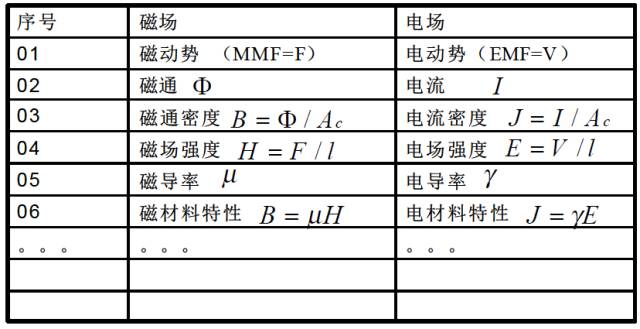
磁学与电学的相似性
磁学与电学的相似性总结成下表:
磁学的基本单位
磁学的基本单位总结成下表:

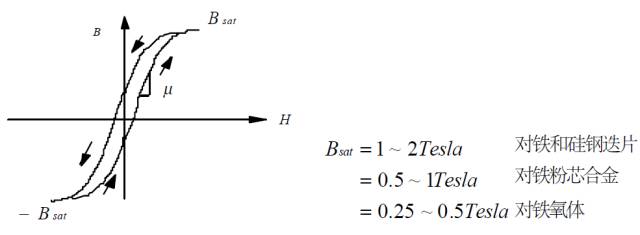
磁芯材料的BH 曲线
典型磁芯材料的 BH 曲线为:
磁路的基本元件—磁阻
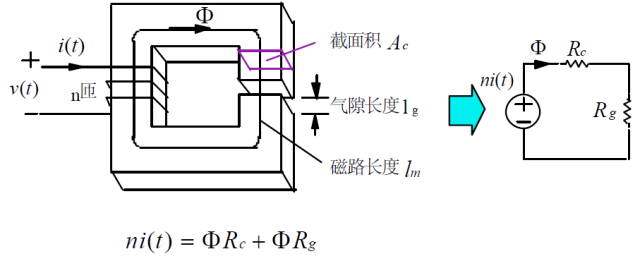
(1):物理结构:
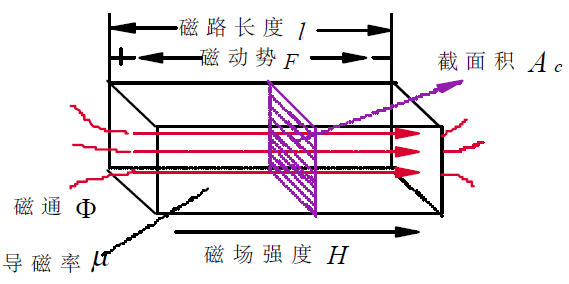
(2):数学关系:
F = ΦR 或磁路欧姆定律:Φ=F/R
其中:R=l/μAc为上述磁路的磁阻。
(3):磁路模型:
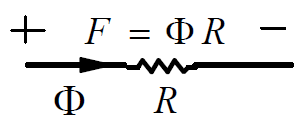
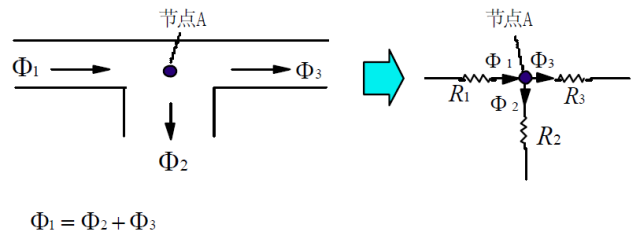
磁路的KCL定律
磁路的 KCL 定律:
进入节点的磁通和离开节点的磁通相等。
磁路的KVL定律
磁路的 KVL 定律:
封闭磁路的磁动势之和为零
复杂磁路的分析步骤
第一步:将实际的磁路画成等效的集中磁路;
第二步:计算各磁路元件的磁阻;
第三步:用磁路 KCL,KVL 定律计算磁通,磁密和磁场强度;
第四步:计算其它的变量。
铁芯的磁滞损耗
(1): 铁芯结构:
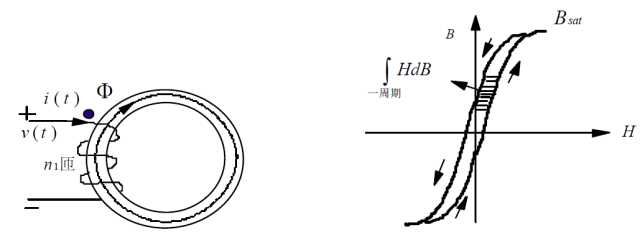
(2): 铁芯的磁滞损耗:
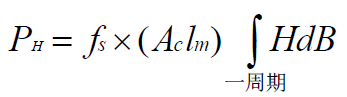
当磁芯材料一定时:
-- 铁芯的磁滞损耗与铁芯的体积成正比;
-- 铁芯的磁滞损耗与激励的频率成正比;
-- 在不同拓扑中,B-H 面积不同,由上式可知:一周期中,因激磁,去磁包围的面积愈大,则磁滞损耗也愈大,故各拓扑(如双正激和半桥)都有最佳工作频率。
铁芯的涡流损耗
(1): 铁芯结构:
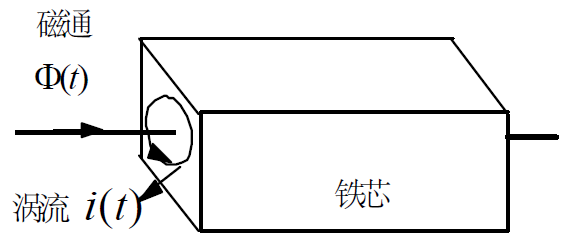
(2): 铁芯的涡流损耗:
原因:铁芯截面的感应电压,如铁芯是电导体,则此感应电压将产生图中所示方向的感应电流。进而在铁芯中产生功耗。
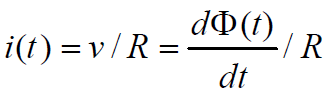
铁芯的涡流,与激励频率成正比,与铁芯的电阻成反比。
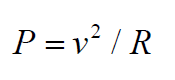
-- 与激励频率的平方成正比,与铁芯的电阻成反比;
-- 高饱和磁密的铁芯,如硅钢片,因涡流损耗,一般只能用作 DC 滤波电感和低频变压器;
-- 高频变压器需要用高电阻率的铁芯,如铁氧体。
实际铁芯损耗的经验公式
经验公式:
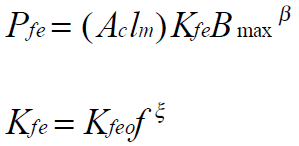
其中:公式中的系数可从铁芯制造商的手册中查得。对于铁氧体:β 在2.6~2.8 之间。
单绕组铁芯元件-电感
(1):物理结构:
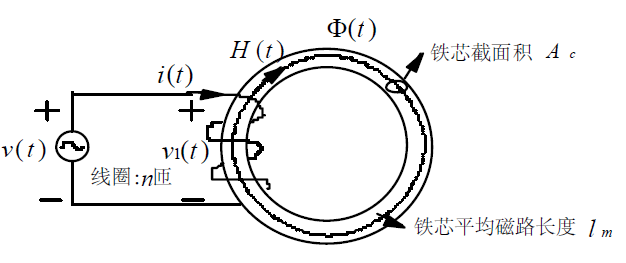
(2):电感量计算公式:
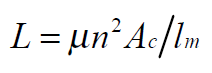
(3):作为直流滤波电感不饱和的条件:
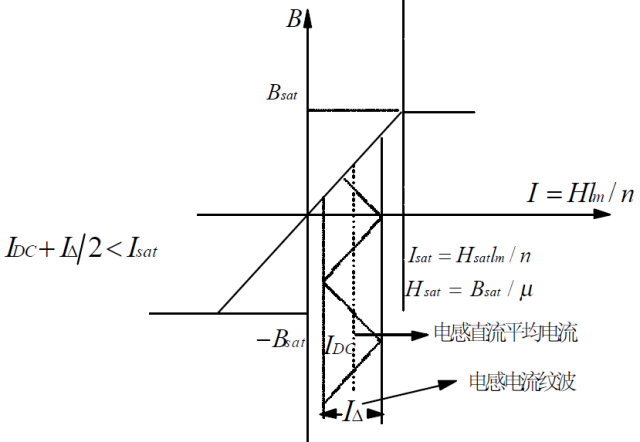
绕组的低频损耗
(1):绕组的低频等效电路:
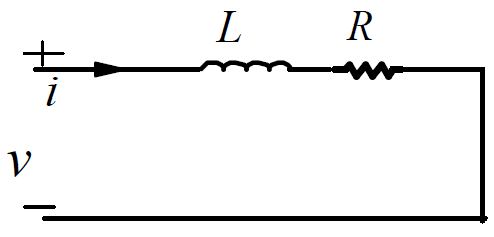
(2):绕组的低频损耗:
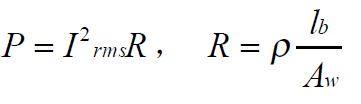
其中: Irms为流过电流的有效值; R 为绕组的低频电阻。
绕组的高频集肤效应
(1):集肤效应示意图:
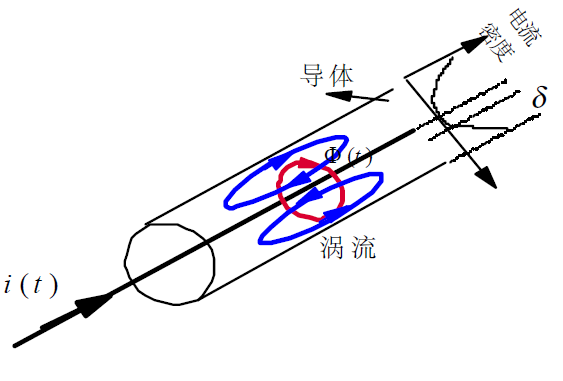
(2):绕组的穿透深度(集肤深度)

其中: ρ为绕组的电阻率, μo 为真空的导磁率。
(3):100°的铜导体,集肤深度为:
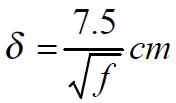
-- 频率愈高,集肤深度愈小;
-- 当导体载有高频电流时,其真正导电的仅仅是表面,故单根导线的线经应小于或等于集肤深
度,否则将浪费材料;
-- 高频时,导体的损耗更大。因电流集中在表面,内部的导体没有导电。
绕组的高频邻近效应
(1):邻近效应示意图:
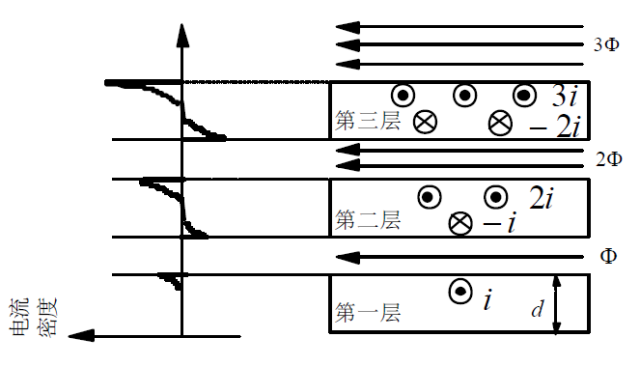
(2):多层绕组总的铜耗
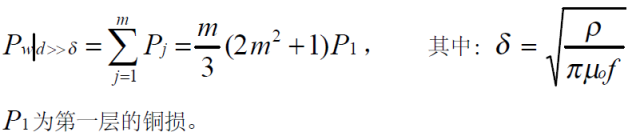
(3):多层绕组的低频损耗:
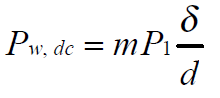
(4):多层绕组的总损耗/低频损耗:
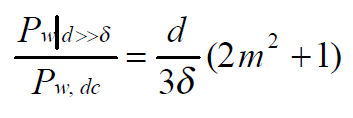




 /4
/4 

