SCARA机械手臂的智能神经网络控制研究
韩晓霞, 谢克明
( 太原理工大学信息工程学院, 山西太原, 030024)
摘 要: 在传统机械手臂动态控制基础上, 将 RBF 神经网络与模糊逻辑控制相结合, 提出 一种新的智能控制方法———RBF 模糊神经网络控制方法。该方法使用两个子网络分别 对关节 1 和关节 2 实施控制, 最后通过协调级网络来消除和减小两个关节之间的耦合 作用。以仿真实验结果说明该网络结构简单明确, 计算更加有效, 并通过适时地修正网 络参数, 在线调整了模糊隶属函数的中心值和宽度, 所设计的控制器能快速、稳定地跟 踪到期望轨迹。机器人不仅可以在粉尘、噪声、有毒、辐射等有害环境下部分代替人去操作, 还能在人所不能及的极限条件下, 如军事、深海、外层空间环境 中完成人所赋予的任务。机器人现已开始进入了家庭和服务行业, 扩大 了人类改造自然的能力, 因此越来越显示出巨大的力量, 成为工业化强 国的竞争焦点。近年来, 随着自动控制理论、电子计算机和航天技术的迅 速发展, 人工智能开始与机器人技术结合, 机器人技术进入一个新的发 展阶段。机器人的轨迹跟踪问题是机器人控制学中一个重要的方面, 在 实际应用中, 往往要求机器人在相当广泛的运行条件范围内, 保持系统 的完善功能和期望特性。对于机器人这样一个复杂的控制系统, 具有非 线性、时变性、耦合的不确定性系统, 存在诸如系统建模误差、高频特性、 机器人各关节的摩擦以及信号的检测误差等不确定性因素, 这些客观存 在的实际情况使得系统控制具有不可避免的困难, 以至于常规的控制方 法无法获得满意的控制性能 。近几年, 越来越多的学者致力于机械臂 的模糊逻辑控制、神经网络控制等智能控制算法。
本文在分析了机械臂神经网络控制的研究现状及应用前景基础上, 提出一种新的智能控制算法———多变量模糊神经网络控制方法, 通过 RBF 神经网络构建了模糊推理, 使神经网络的节点、连接权值具有明确 的物理意义, 能够在线调整模糊隶属函数的中心值和宽度。同时, 引入的 协调级网络, 有效地消除了机械臂关节之间的耦合作用。仿真实验表明 该控制器具有很强的自学习能力, 并可以消除系统动力学模型的不确定 性和外部干扰的影响, 通过控制算法适时地修正网络参数, 实现了连续 轨迹跟踪控制, 具有良好的控制品质, 可实现对非线性系统任意轨迹的 轨迹跟踪控制。
1 神经网络在机械臂动态控制中的应用
神经网络自身的特点, 特别适用于像机器人这样具有复杂性、高度 非线性、多变量、强耦合且严重不确定的大系统的控制。首先, 由于神经 网络在许多方面试图模拟人脑的功能, 因此神经网络控制并不依赖精确 的数学模型, 并且神经网络对信息的并行处理能力和快速性, 适于机器 人的实时控制。其次, 神经网络的本质非线性特性为机器人的非线性控 制带来了希望。神经网络可通过训练获得学习能力, 能够解决那些用数 学模型或规则描述难以处理或无法处理的控制过程。第三, 神经网络还 具有很强的自适应能力和信息综合能力, 因而能同时处理大量的不同类 型的控制输入, 解决输入信息之间的互补性和冗余性问题, 实现信息融合处理。
机器人神经网络控制主要应用在机器人路径规划和运动控制两方面, 利用神经网络来对非线性对象进行建模, 或充当控制器, 或优化计 算, 或进行推理, 或故障诊断等, 以及同时具有上述某些功能的适应组合, 并提出了各种基于神经网络的机器人控制方法, 包括神经网络逆 模控制, 神经网络内模控制以及神经网络自适应控制等, 取得了很多研究成果。
随着智能控制技术的发展, 神经网络与专家系统、模糊控制、进化算法以及 H∞ 控制理论相结合构成机械臂的智能神经网络控制成为研究的 热点。在机器人动态控制中使用最多的就是模糊神经网络和 H∞ 鲁棒神 经网络。其中模糊神经网络是具有推理归纳能力的神经网络, 它利用神 经网络可以逼近任意非线性函数的特性来模拟模糊控制的推理方法而 构造出来, 同时神经网络具有自学习能力, 使得模糊神经网络的推理方 式在实际的控制过程中是可以不断修正的。同时, 由于模糊神经网络的 结构具有明确的可用语言形式描述的物理意义, 使得模糊神经网络的结 构设计和权值初始化非常容易。由于神经网络具有多种结构和学习算 法, 模糊逻辑也具有多种形式, 二者结合的实现形式是研究工作的重点和难点。本文基于 RBF 神经网络与模糊逻辑具有函数等价性, 提出 了 RBF 模糊神经网络, 实现了神经网络与模糊逻辑控制的有效结合。
2 跟踪问题描述与动力学模型
本文的实验设备是固高 GRB400 工业机器人, 结构形式为 SCARA 型平面关节( 见图 1) , 是具有 4 个关节的搬运机器人。其中关节 1 和关 节 2 是回转关节, 具有 2 个自由度, 完成坐标系 X—Y 平面的运动; 关节 3 是直线关节, 通过丝杠连接完成坐标系 Z 轴方向的运动( 上下运动) ; 关节 4 为旋转关节( 手腕的 运动) , 用来调整工具的角 度。机器人末端工具的开闭 利用控 制 器 的 直 接 数 字 量 输出控制, 理论上可以同时 控制 16 路工具。在 GRB400 机器人 末 端 预 装 了 电 磁 手 爪, 还可以根据实际作业的 需要加 装 简 单 的 电 磁 手 爪 或气动手爪。其中关节 3、关 节 4 与关节 1、关节 2 是完 全解耦的, 而关节 1、关节 2 之间是耦合的。本文主要是 解 决 关 节 1 和 关 节 2 的 平 衡问题, 通过设计模糊神经网络伺服控制器, 使其动力学性能更好, 实现 连续的轨迹跟踪。

( 1) 式中: M( Θ) 被称为惯性矩阵; V( Θ, Θ! ) 称为离心和哥氏力项; F( Θ) 是静态和动态摩擦矩阵; G( Θ) 表示重力效应; T(d Θ, Θ! ) 代表由所有负荷 变化或建模误差所引起的扰动。
忽略系统的摩擦和不确定性因素时, 系统的标称模型的动力学方程 可以表示为: τ=M( Θ) Θ# +V( Θ, Θ! ) Θ! +G( Θ)
( 2) 式中: 一律用 ci 表示 cosθi, si 表示 sinθi, cij 表示 cos( θi+θj) , sij 表示 sin ( θi+θj) 。其中, l1, l2 分别表示关节 1、关节 2 的长度; lc1, lc2 分别表示关节 1、 关节 2 的质量中心到转动中心的距离; I1, I2 分别表示关节 1、关节 2 的转 动惯量; Θ=[ θ1 θ2] T, τ=[ τ1 τ2] T。
M( Θ) = M11 M12 !M21 M22", V( Θ, Θ) = υ11 υ12 !υ21 0 ", G( Θ) = 0!0"
M11=m1·l2c1+m2·( l21+l2c2+2l1·lc2·c2) +I1+I2;
M22=m2·l22+I2; M12=M21=m2·( l2c2+l1·l2·c2) +I2; υ11=( - m2·l1·lc2·s2)·θ" 2
υ12=( - m2·l1·lc2·s2)·θ" 1+( - m2·l1·lc2·s2)·θ" 2; υ21=m2·l1·lc2·s2·θ" 1
3 RBF 模糊神经网络控制器结构及算法实现
3.1 具有协调级的 RBF 模糊神经网络控制器结构
固高机械臂是 MIMO 系统, 根据系统的动态控制特点, 本文设计了 一种具有协调级的多变量 RBF 模糊神经网络, 见图 2。该网络是四输入 二输出的网络, 由三部分组成: 前件网络、后件网络和协调级。前件网络 和后件网络分别是对机械臂关节 1 和关节 2 进行计算的, 协调级网络对 两个子网络进行综合。网络的主要计算由前件网络来完成, 其中两关节 的位置误差 e1 和 e2, 以及关节误差变化率 ec1 和 ec2 四个变量分别作为网 络的两个子网络的输入; 输出为关节 1、关节 2 的控制量 u1 和 u2。
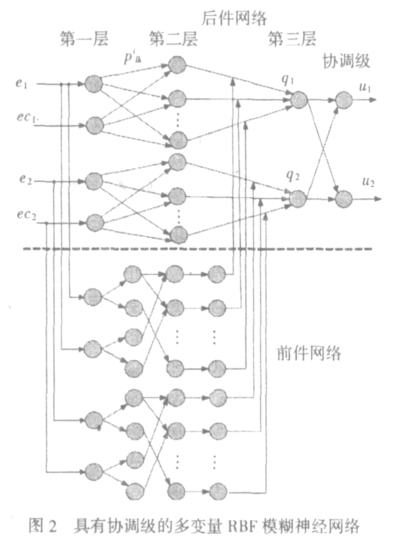
前件网络采用 RBF 神经网络结构, 其中, 输入层中使用径向基函数 ( RBF) 作为激活转移函数,将连续的输入数值变换成具有不同模糊标 记, 如“高, 正, 零, 负, 低”的模糊隶属度。通过适时地修正网络激活函数 的参数, 可以在线调整模糊隶属函数的中心值和宽度。中间层体现形如 “if x1 is a, x2 is b, then y is c”的乘积模糊规则, 权值为 1, 采用 Takagi- Sugeno( T- S) 网络结构, 即每个输出是两个前提的乘积, 确定子网络的每 条模糊规则的适应度。输出层为 RBF 网络的激活函数是线性函数, 即对 每个输入进行加权后求和。
后件网络是输入的多项式, 用来计算每一条规则的后件, 并计算系 统的输出, 实现线性组合。输入的结点数等于给定输入量的模糊等级数, 每一个结点则代表一条规则。后件网络的调整参数为网络连接权值 pilk,v> 当各自进行完匹配后, 输出为 q1, q2, 然后进入协调级。
协调级是由单层神经网络构成, 它的作用就是对两路控制作用进行 综合, 通过调整神经元的权值来消除关节 1 和关节 2 之间的耦合, 以达 到多变量控制, 输出为 u1 和 u2。神经元采用 S 型函数, 连接权系数为 vig, i 为输出变量的个数, 控制器输出为: ui=(f si) =f 2 i = 1 $#qivig%=1(/ 1+e- μsi) ( 3)
3.2 RBF 模糊神经网络控制器的算法实现步骤
步骤 1: 分别确定两个关节 1、关节 2 网络中 e 和 ec 的隶属度划分; 选定两个子网络各自的隶属度划分中的中心值 C 和宽度△的初值; 以及 各后件网络的权值 P 的初值; 选定协调级中的权值 V 的初始值; 选定隶 属函数的学习速率 &c, &’, 后件网络中连接权值的学习速率 &p 以及协调 级中权值系数的学习速率 (。大写表示矩阵, 取 t=1。
步骤 2: 采样得到关节 1、关节 2 的两个给定值 "(1 0) 和 "(2 0) , 及两 个子系统输出 "d1, "d2, 计算误差 e(1 t) , e(2 t) 及误差的变化 ec(1 t) , ec(2 t) 。
步骤 3: 计算得到模糊神经控制器的控制输出 u1, u2, 进行控制和计 算。
步骤 4: 计算目标函数 E= 12( yri- yi) 2, yri, yi分别表示系统的期望输出 和实际输出; 并修正协调级权值系数的学习速率 (; 计算修正各子网络 的隶属度的中心 C、宽度△和权值 P。
步骤 5: 设置 t=t+1, 取下一个采样点, 返回步骤 1 进行计算。
4 仿真及实验结果
本文对关节 1、关节 2 进行仿真实验, 动力学模型如式 ( 2) , 固高 GRB400 机械臂的结构参数 m1=1.331 kg, m2=0.482 kg, l1=200 mm, l2=200 mm, I1=1.385×10- 2 kg·m2, I2=5.737×10- 4 kg·m2。输入变量 e1, ec1, e2, ec2的隶 属函数的划分均为{ 正大, 正小, 零, 负小, 负大} ; e1, e2和 ec1, ec2隶属度中 心值分别取 C1=C2=[ 3, 1.5, 0, - 1.5, - 3] , C1=C2=[ 1, 0.5, 0, - 0.5, - 1] , 宽度 △1=△2=[ 1, 1, 1, 1, 1] 。取θ"(1 0) =θ"(2 0) =0 rad/s, 采样周期为 0.000 5 s, 权系 数 P1 的初始值都选为 1; 协调级的权系数矩阵 V 的初始值选为单位阵; 机械臂关节 1 的学习速率为: β1c=0.55, β1σ=0.31, β1p=0.22; 机械臂关节2的 学习速率为: β2c=0.6, β2σ=0.3, β2p=0.1。
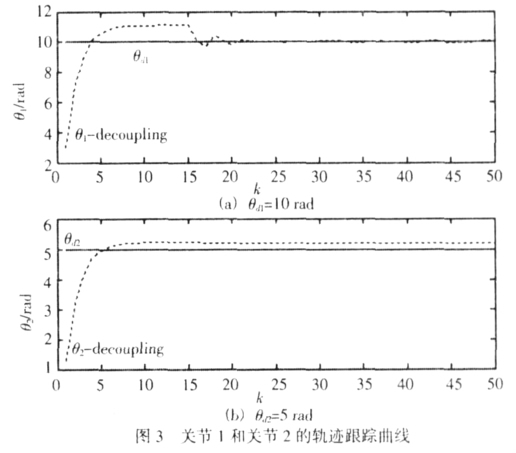
图 3 所示为关节 1、关节 2 在控制算法完成 50 次迭代后, 绘制的跟 踪曲线图。由图 3 可见, 学习算法进行到 20 次的时候, 控制器的跟踪轨 迹就和期望轨迹重合。仿真结果表明控制器具有良好的跟踪特性, 能消 除关节变量之间的耦合作用, 使关节 1、关节 2 能分别快速跟踪到期望位置。
5 结语
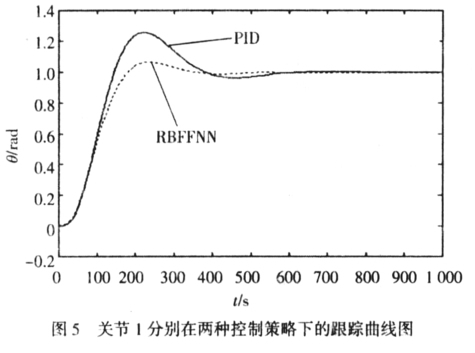
仿真实验结果表明,RBF模糊神经网络控制算法能以较少的网络训练次数达到满意的跟踪特性,具有良好的鲁棒性和抗干扰性能,可实现机械臂这类具有重复运动性质的非线性对象的轨迹跟踪控制。




 /2
/2 
