PSpice已经成为模拟电路仿真使用的行业标准工具。模拟电路具有真实的物理实现,可以用它们的原理示意图进行仿真,其频率响应是电路时间常数的结果。与之相反的是,数字滤波器对一系列样本进行数学运算。
数字滤波器的时间常数隐藏在采样间隔T中。因此数字滤波器一般是通过它们的传递函数进行数学仿真,而且为了做到这一点,能够方便地仿真由采样率fs引起的采样延时T=1/fs非常重要,因为这个延时定义和衡量了整个滤波器的响应性能。通常拉普拉斯变换用于模拟电路的行为建模,因为它将时域变换成为复频率s域。数字滤波器的频率响应作为一个特殊例子,可以从拉普拉斯变换的时移理论(延时理论)推导出来。该理论表示,如果时间函数f(t)在时域中被延时了时间T,那么在频域中的结果要乘以e-sT,见公式(1)。
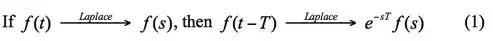

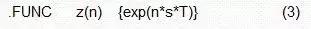
图1:交流线干扰平均器的PSpice原理图(梳状滤波器)。
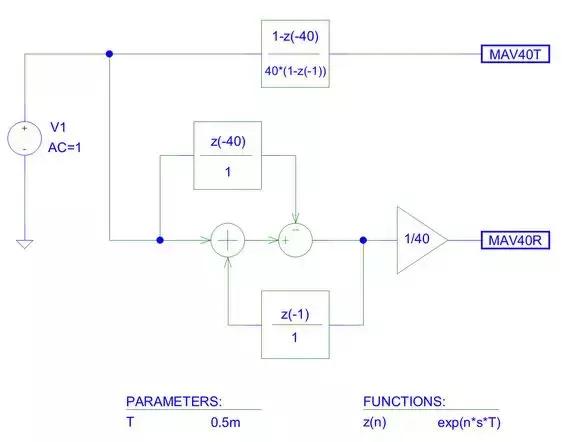
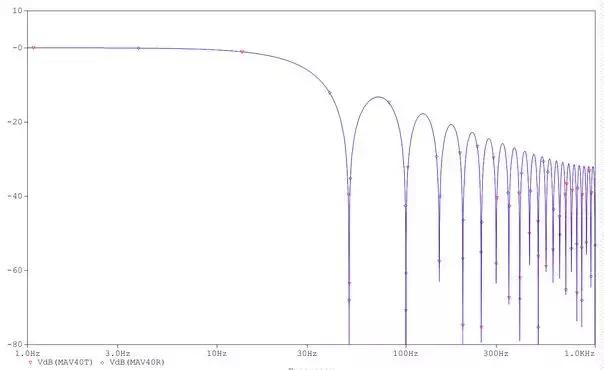
举例来说,假设采样频率fs = 2kHz或T = 0.5ms。为了抑制50Hz的电力线(PL)干扰,来自同一个周期的样本必须被平均处理。在2kHz采样率时,一个电力线周期由20ms/0.5ms = 40个样本组成。平均器可以用传递函数直接仿真(输出MAV40T),或借助接近于其实际算法实现的结构并利用延时模块、增益模块以及和差结点进行仿真 (输出MAV40R)。该仿真在电力线干扰的所有谐波处都有凹槽,如图2所示。
图2:平均器的频率响应。
来源:网络






 /1
/1 

