傅里叶级数傅氏篇章2
傅里叶变换和逆变换应用之一是数字滤波电路分析原理。篇章2,正传-傅里叶级数。
有这样的一个结论:“任何周期函数都可以用收敛的正弦级数表示”[1]。意思上任何(非正弦)周期函数都可以分解为三角级数的线性组合。反过来,三角函数的线性合并起来可以为各种各样的周期函数(非正弦),比如锯齿波、方波、半波、全波等等函数。在满足收敛性质的三角函数是可以组合为任何周期函数,其中的三角函数是傅里叶级数延拓的展开形式。
按照傅里叶级数的三角形式表示或者一般表示:
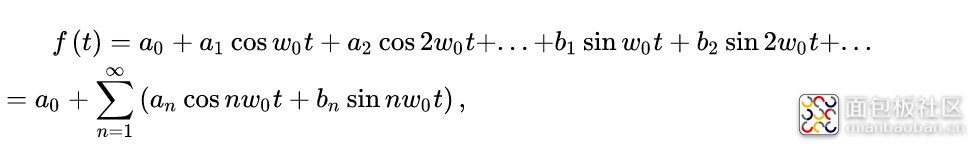
按照傅里叶级数的复指数形式表示:
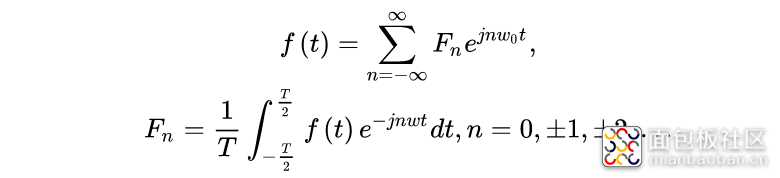
在实际的分析和调试里,应该更方便复指数形式应用,这里只要讨论时域波形的叠加。

[此图片来源于书籍,顾樵(Qiao GU),Mathematical Methods for Physics]
可以看出傅里叶级数在周期内的每一个连续点或者间断点(离散范畴)存在有定义的值;周期为2π的,在(0, 2π)内对这些三角函数定积分证明这些三角函数在0-2π内存在正交。2π刚好是一个完整圆,这些三角函数对应的圆形是缠绕在一起。
两个波形合并之后,波形的改变。
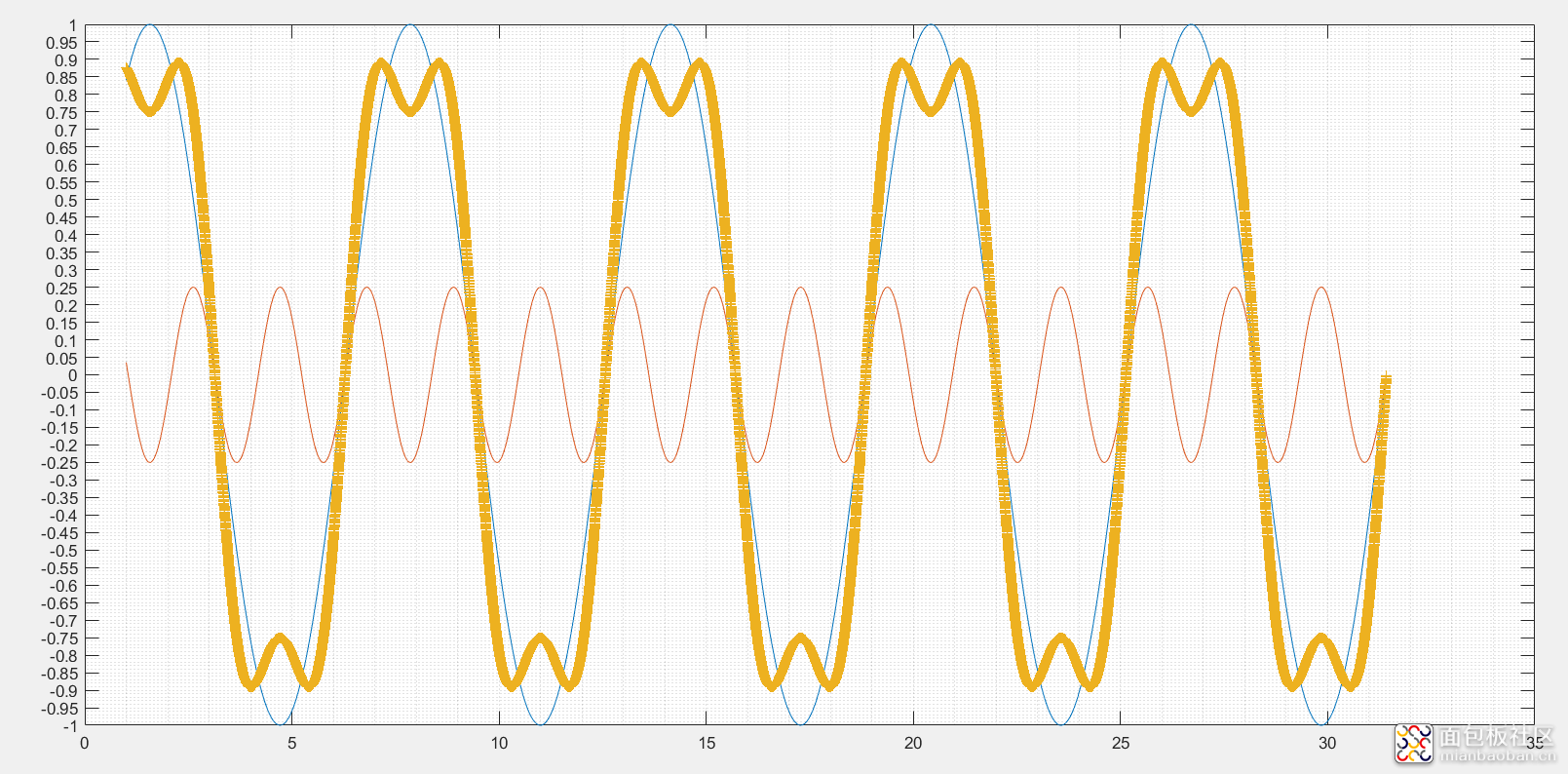
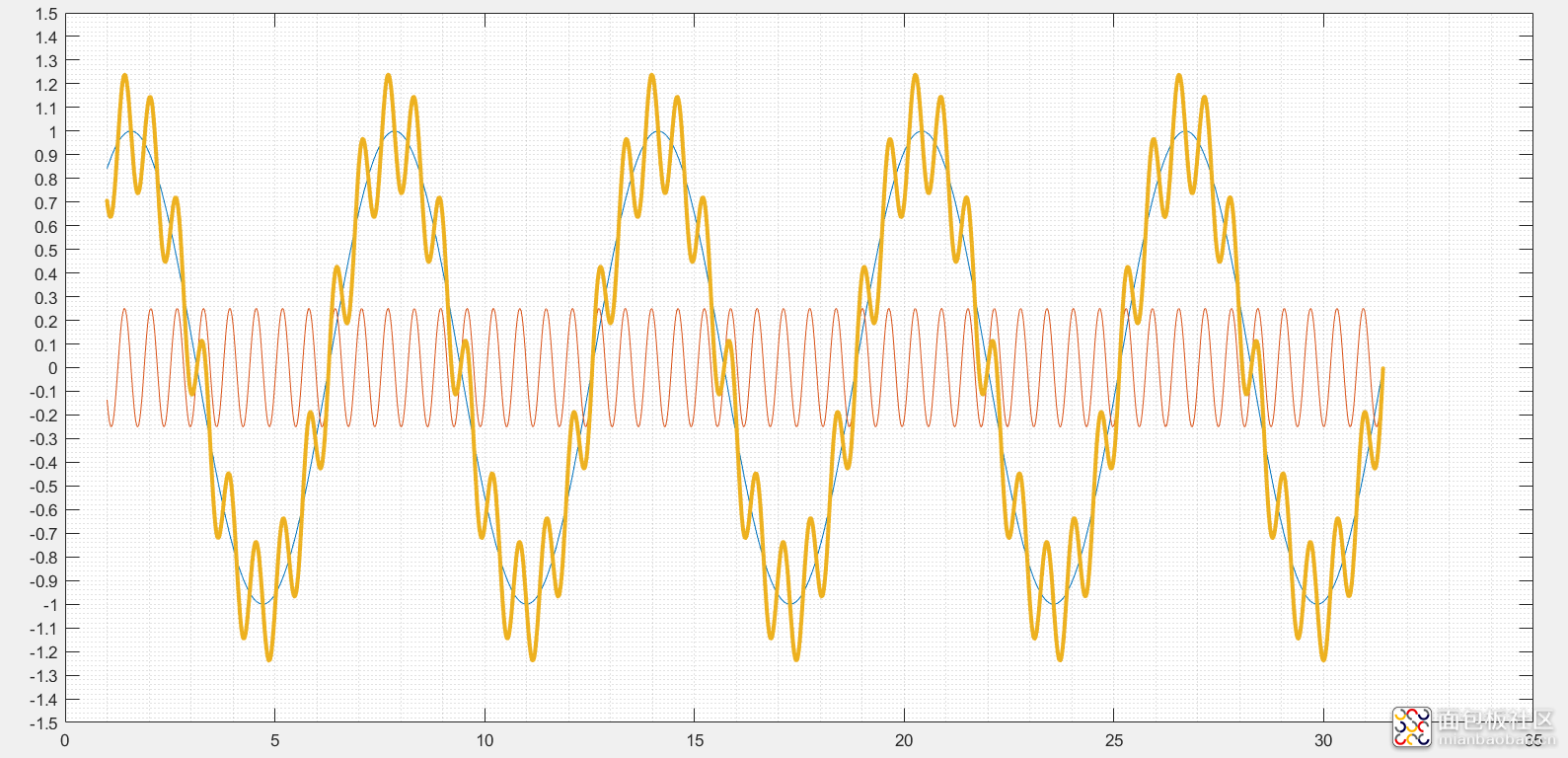
某一段时域点上对应的是某一个区域(x1, x2],两个波形都是递增状态,那合成的波形就是增幅的;反之,都是递减状态,那合成的波形幅度就是衰减的;一个递增和一个递增,由幅度决定。这里的波形合并都是以+,不包含-,不反相,都是0电位以上。
降幅还是升幅,是+-、--、++、-+的一个过程,同相相加,方相相减,。然而三角函数明显的特征就是周期性、奇偶性,幅度大小、周期性的递增和递减。
这里分析下傅里叶级数,首先在项目上我还没有遇到过要用到傅里叶级数的应用,可能类似正弦波混杂一些高次谐波导致失真的情况就有而出现。
这里只要实验下傅里叶级数数学性质,增强电路里的数学知识,(软件:MATLAB)。
代码非常简单易截图形式。
1、 基波混杂低谐波的波形情况
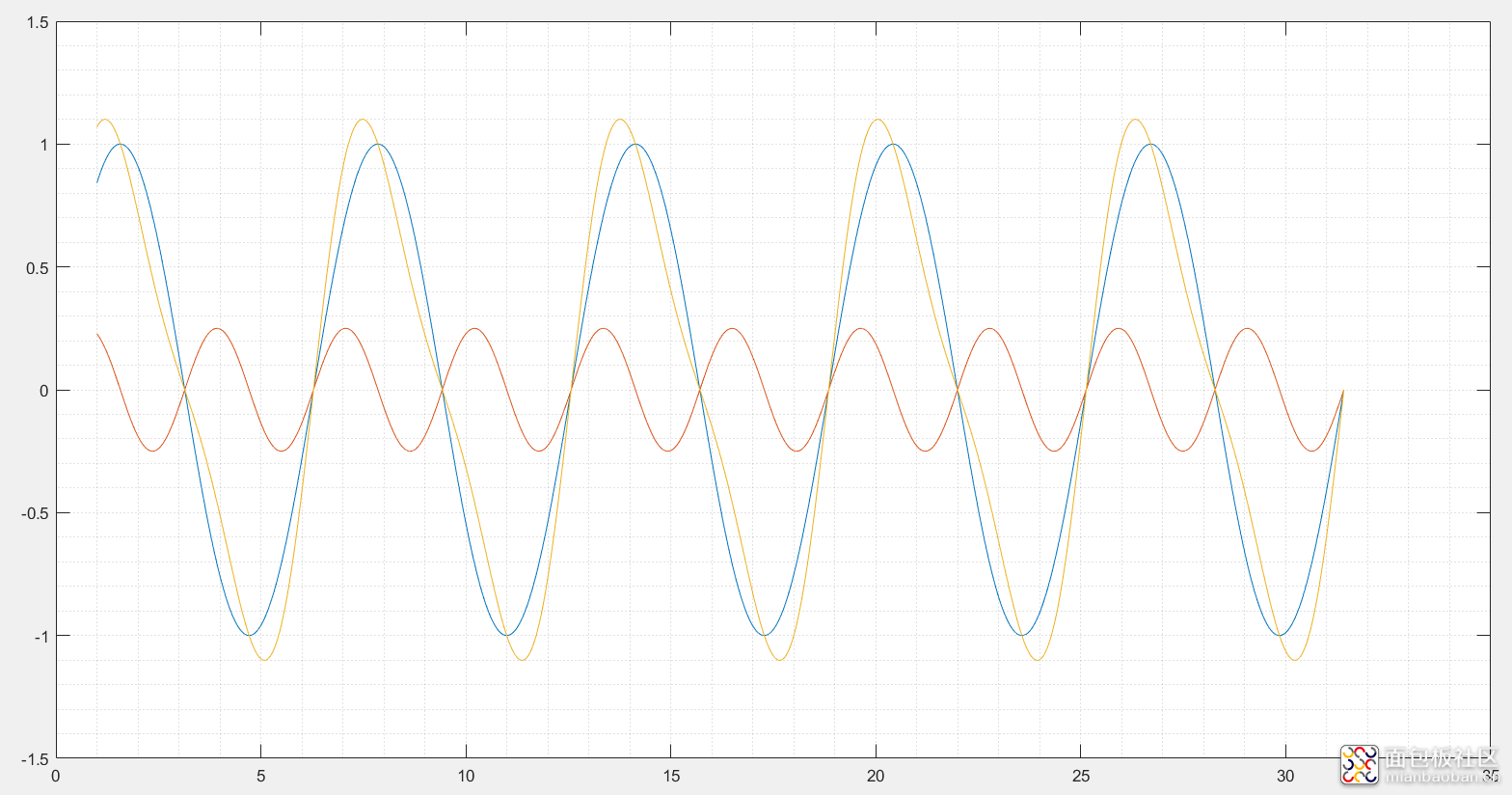

2、基波混杂高谐波的波形情况
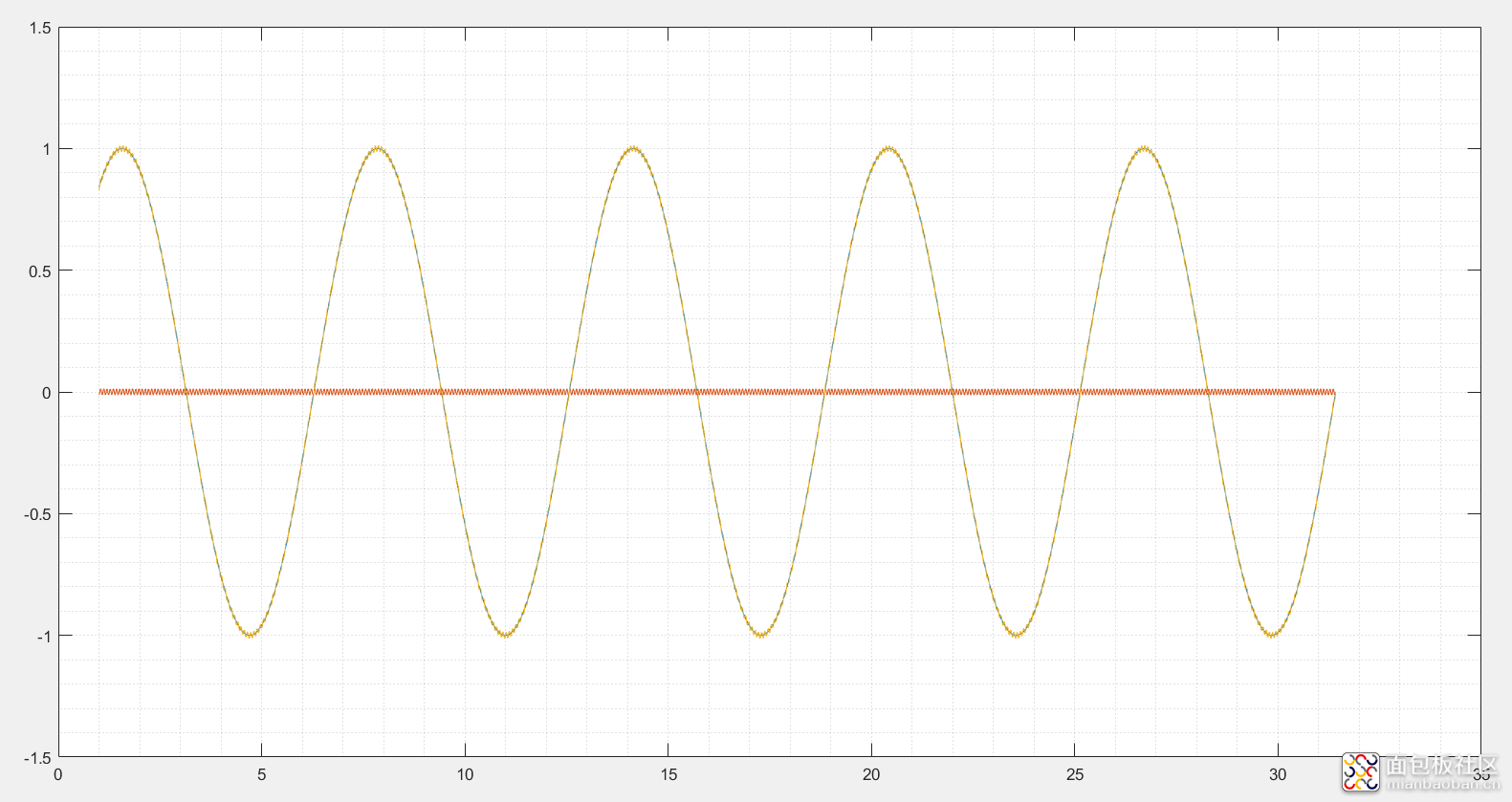

3、奇函数的傅里叶级数组合
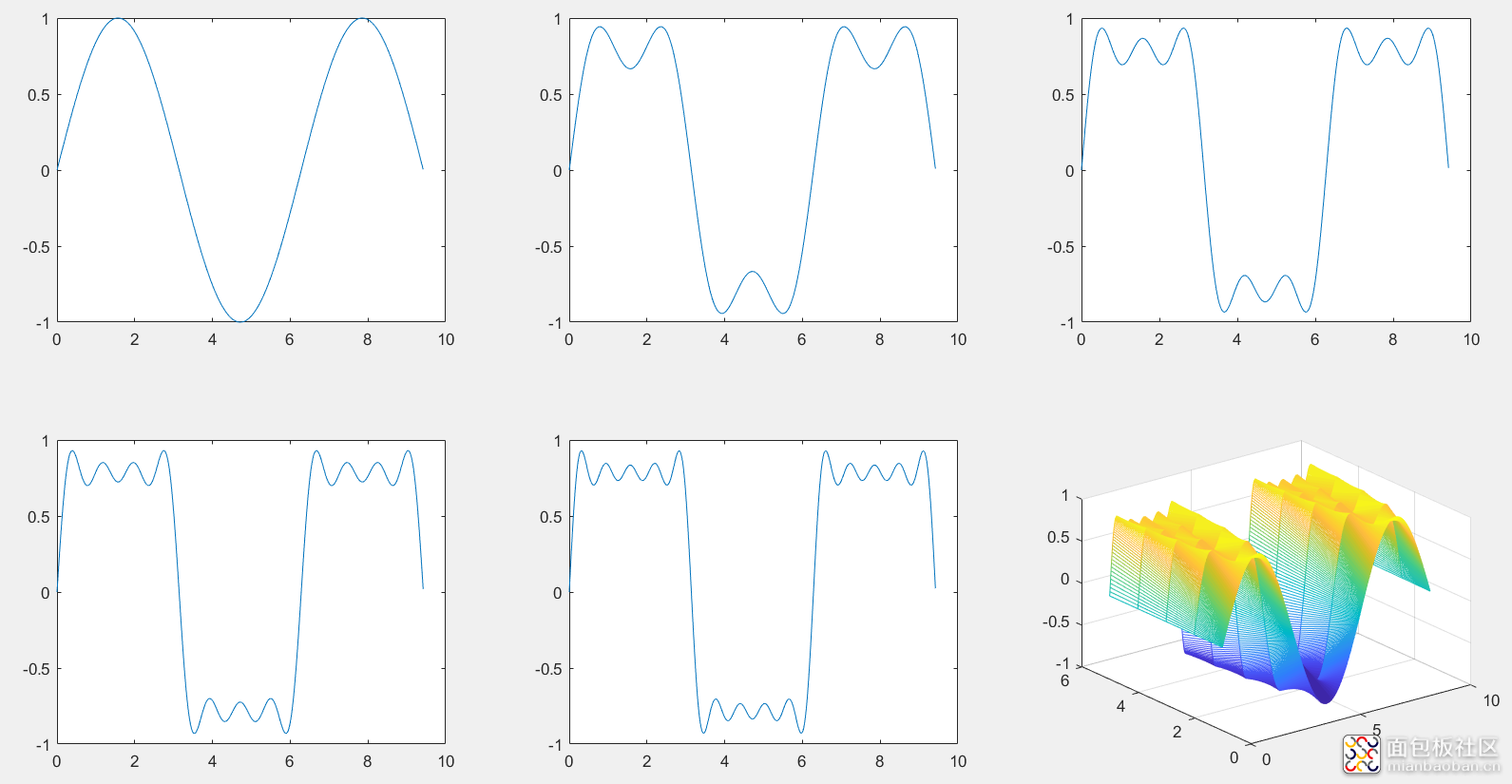

4、偶函数的傅里叶级数组合
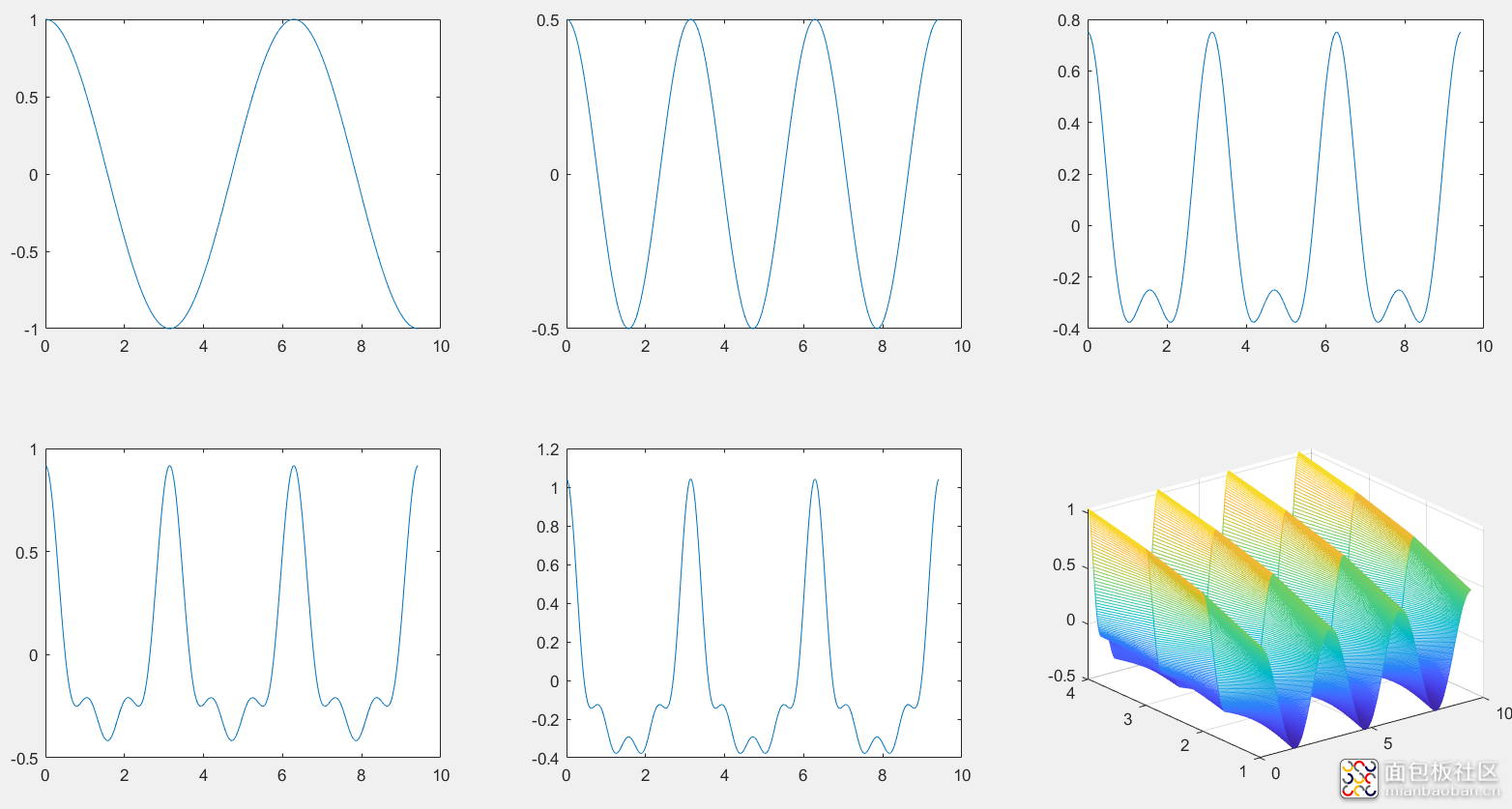
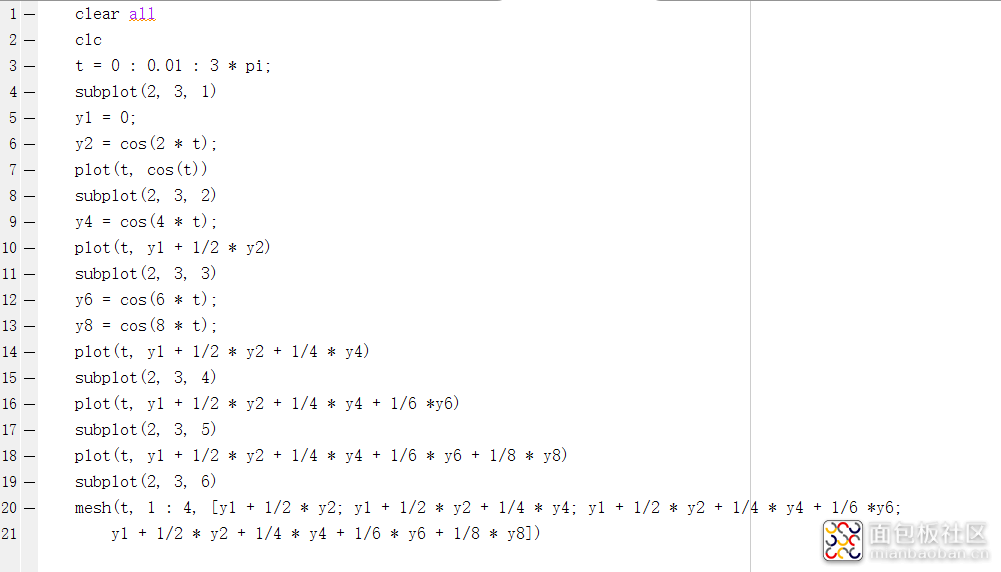
目的,加深了数学知识在电路中的运行过程。
参考文献
【1】【德】顾樵(Qiao GU).数学物理方法=Mathematical Methods forPhysics[M].北京:科学出版社,2012
【2】李献,骆志伟,于晋臣.MATLAB/Simulink系统仿真[M].北京:清华出版社,2020.1
【3】燕庆明,于凤芹,顾斌杰.信号与系统教程.北京:高等教育出版社,2016.12
【1】【德】顾樵(Qiao GU).数学物理方法=Mathematical Methods forPhysics[M].北京:科学出版社,2012
【2】李献,骆志伟,于晋臣.MATLAB/Simulink系统仿真[M].北京:清华出版社,2020.1
【3】燕庆明,于凤芹,顾斌杰.信号与系统教程.北京:高等教育出版社,2016.12
代码目录:
clear allclc t = 0 : 0.01 : 3 * pi; subplot(2, 3, 1) y1 = 0; y3 = sin(2 * t); plot(t, y1 + 1/2 * y3) subplot(2, 3, 2) y5 = sin(4 * t); plot(t, y1 + 1/2 * y3 + 1/4 * y5) subplot(2, 3, 3) y7 = sin(6 * t); plot(t, y1 + 1/2 * y3 + 1/4 * y5 + 1/6 *y7) subplot(2, 3, 4) plot(t, y1 + 1/2 * y5 + 1/6 *y7) subplot(2, 3, 5) %plot(t, y1) %plot(t, y1 - 1/3 * y3 + 1/5 * y5 + 1/7 *y7) %subplot(2, 3, 6) mesh(t, 1 : 3, [ y1 + 1/2 * y3; y1 + 1/2 * y3 + 1/4 * y5; y1 + 1/2 * y3 + 1/4 * y5 + 1/6 *y7])
复制代码站在前辈们铸筑每一座座阶梯上,我心怀感激。阅读、汇总、归纳前辈们的知识成果,我很幸运。





 /5
/5 


