大家都喜欢转发《世界上最伟大的N个公式》,其实只能搞清楚“勾股定律”和“圆周率”公式。
一般第一的“麦克斯韦方程组”,只能围观围观。所以,如果你不懂麦克斯韦方程组,他再伟大,都与你无关。
【麦克斯韦方程组的数学形式】
在电磁场的实际应用中,经常要知道空间逐点的电磁场量和电荷、电流之间的关系。从数学形式上,就是将麦克斯韦方程组的积分形式化为微分形式。
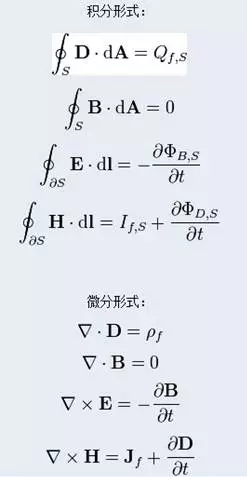
上面的微分形式分别表示:
(1)电位移的散度等于该点处自由电荷的体密度 (高斯定理) 。
(2)磁感强度的散度处处等于零 (磁通连续性原理) 。
(3)电场强度的旋度(法拉第电磁感应定律)等于该点处磁感强度变化率的负值;
(4)磁场强度的旋度(全电流定律)等于该点处传导电流密度 与位移电流密度 的矢量和;
由于电磁场抽象,矢量场的数学理论没有在一些大学课程展开。对于散度、旋度、梯度完全没有概念。这也是当年学了之后,没有理解到位,或者印象不深的一个原因。
【矢量场不好理解,我们来看流量场】
1、通量
下图中,右侧的圆环,有一定面积。左侧的磁铁,它的磁感应线,磁感应强度一定。这个圆环内的,磁感线的总数,随着磁铁的运动,而变化。那么这个磁通量就变化了。
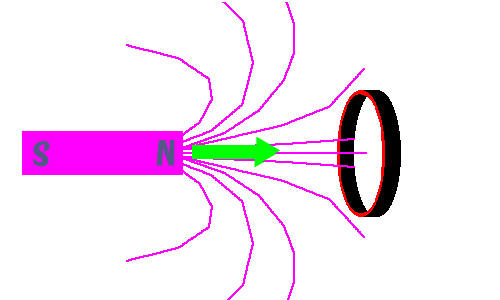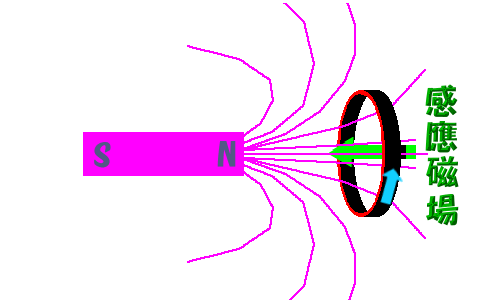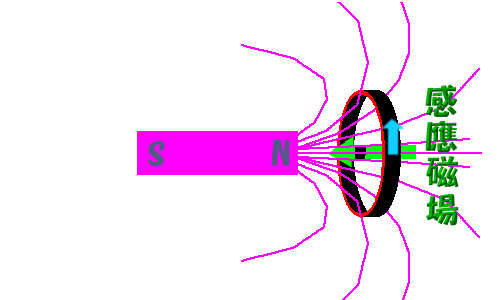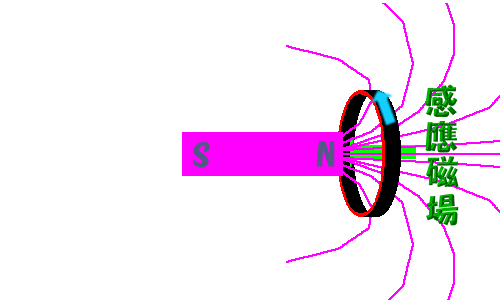
我们看到,磁场密度变化,或者面积变化,那么磁感线的总数自然变化。那么,我们改变圆环与磁铁的角度。磁感应线也会变化,这个就是磁通量的变化。
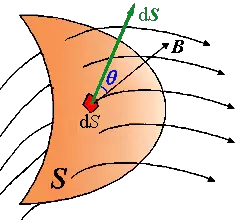
对比于流量场,也很简单。当我们拿个一个方形的铁框子,放在一个湍急的流水里面。当我们改变水流的速度,或者改变框子的大小,或者改变框子的角度。都会影响从框子中间流过的流量。
Φ=BS,适用条件是B与S平面垂直。如图,当S与B的垂面存在夹角θ时,Φ=B·S·cosθ。
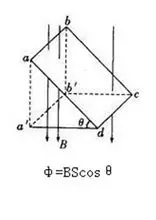
用矢量的方式,表示,就是这个公式:
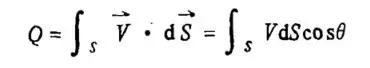
2、我们在一个封闭的面积里面去度量“通量”,本质在描述这个封闭空间的“聚”还是“散”。

这个一个漏水的桶。我们用一个红色的圆圈,框住这个桶,描述一个椭球形的空间。
如果,流进桶的水量,大于,漏出去的水量。我们认为,这个桶在聚水。
如果,流进桶的水量,小于,漏出去的水量。我们认为,这个桶在散水。
如果,流进桶的水量,等于,漏出去的水量。我们认为,这个桶,既没有“散”,有没有“聚”。
我们看这个封闭面积的通量,就知道,这个面积内的聚散程度。
3、散度
我们把上面那个桶,想象成无限小。则,通过这个封闭面积的通量,与这个封闭面积的体积,之比,我们就认为是在这点的“散度”。
矢量场的散度,是个标量,可以理解为:穿过包围单位体积的闭合曲面的通量。所以散度又被称作:通量源密度。

是对某一个区域的通量,无限小的情况下的描述,也就是空间上,某一点的通量的描述。我们把大桶,想想成好多个小桶。我们的散度,就是描述无限小的小桶的“散聚”程度的物理量。
对于静电场来说,有电荷存在的点,其散度一定不为零。
对于恒定磁场而言,都是闭合的曲线,没有类似于“电荷”的“磁荷”的概念。所以恒定的次创,是无源场,也就是每一个点的散度都为零。
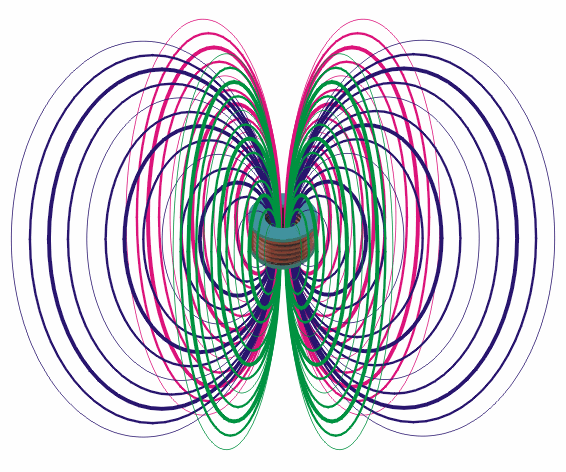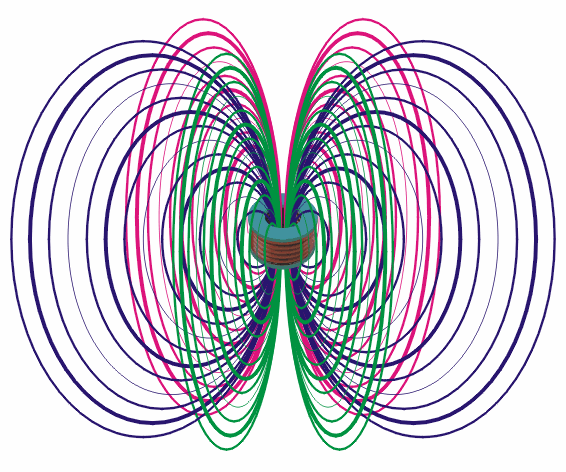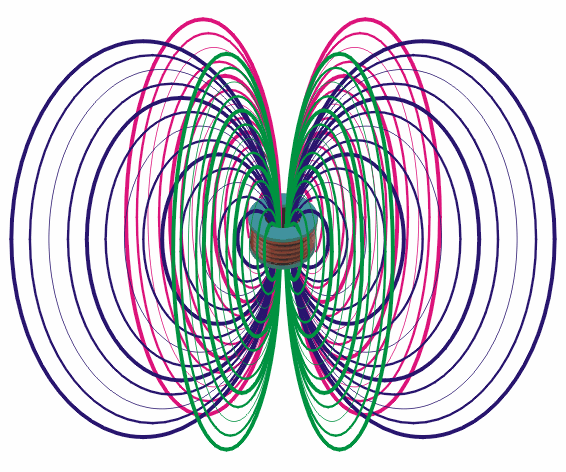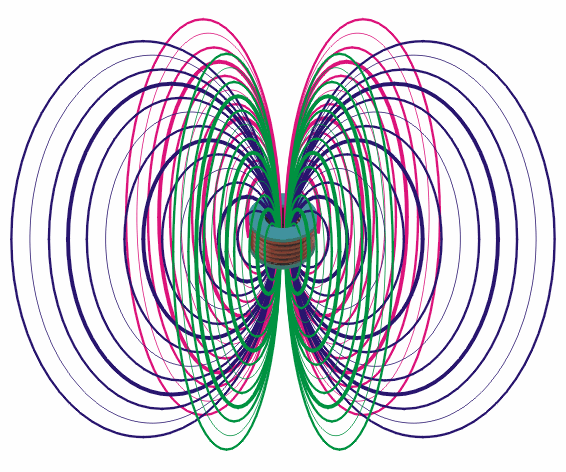
1、磁感强度的散度处处等于零 (磁通连续性原理) 。
2、电位移的散度等于该点处自由电荷的体密度 (高斯定理) 。

这时,我们再来看看这两个公式,是不是觉得很好理解,也倍感亲切?
恭喜你,伟大的麦克斯韦方程组,你已经懂一半了!
4、环流

既然是旋度,我们故名思议,是度量旋转的一个物理量。
我们根据散度物理意义, 散度, 就是是否有源,可以推测:旋度也正是"描述矢量场中某一点所包含微元在场中的旋转程度".
同样,我们先理解一下什么是“环流”:
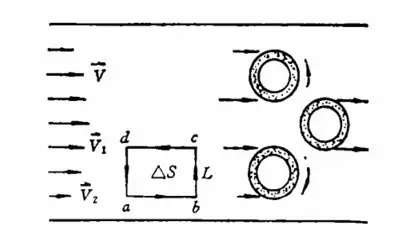
环流:弯道水流的内部呈螺旋状运动,在横断面上的投影呈环形的水流。
对于我们描述电磁场来说:环流是,区域ΔS内有无涡旋的度量。
根据上图中,我们对环绕ΔS的四个边的流速进行积分,得到:
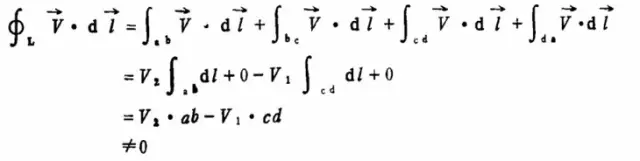
如果V2=V1,则这个积分结果为0,则这个面积内,没有涡流。
如果V2≠V1,则这个积分结果不为0,则这个面积内,有涡流。
5、旋度
环量和通量一样,是描述向量场的重要参数。某个区域中的环量不等于零,说明这个区域中的向量场表现出环绕某一点或某一区域旋转的特性。旋度则是局部地描述这一特性的方法。为了描述一个向量场在一点附近的环量,将闭合曲线收小,使它包围的面元
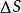
的面积趋于零。向量场沿着
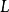
的环量和面元的比值在趋于零时候的极限值:
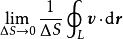
我们一样把整个场,在每个点去考察他的环量,并除以这个点的面积。则得到这个点的旋度。
对于静电场来说,电场强度沿着空间任意封闭曲线的环量,都为零。我们称为无旋场。
对于恒定磁场来说,有些地方有漩涡流,我们称之为有旋场。
我们来看宏观的“法拉第电磁感应定律”
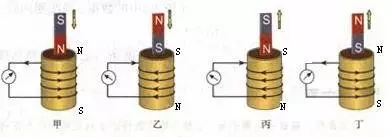
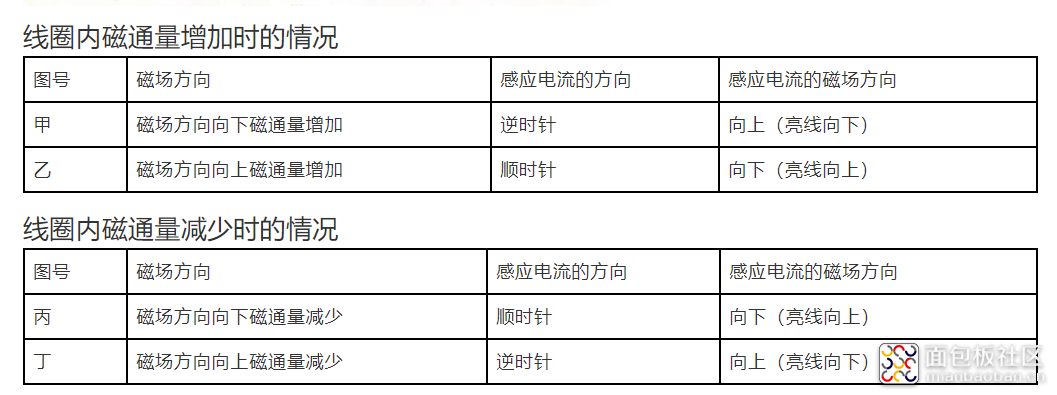
麦克斯韦将安培环路定理推广为全电流定律,是电磁场的基本方程之一 。其内容为:任意一个闭合回线上的总磁压等于被这个闭合回线所包围的面内穿过的全部电流的代数和。
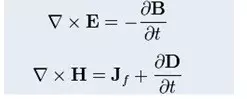
此时再看这两个公式,你也会觉得有点感觉。
一位同学(当年的学霸,现在中科院的博士)提醒,先把旋度和散度讲清楚。所以想理解麦克斯韦方程组之前,本文重点先把“旋度”和“散度”的概念讲清楚。
“我确信已我发现了一种美妙的讲法把麦克斯韦方程组讲清楚 ,可惜这里空白的地方太小,写不下。”
来源:硬件十万个为什么







 /5
/5 


