一、实践目的
1、利用计算机作典型环节和开环系统的波特图、极坐标图和尼尔科斯图。
2、观察记录控制系统的开环频率特性。
3、控制系统的开环频率特性分析。
二、实践内容1、绘制开环系统
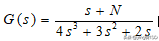
的BODE图,计算出该系统的稳定裕度, 并判断闭环系统的稳定性。【N=135】
2、作开环系统
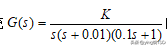
的波特图、奈奎斯特图和尼尔科斯图,记录并观察曲线,依此分析闭环系统的性能。【K=13.5】
3、系统开环传递函数为:
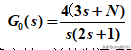
做出nyquist图,按nyquist稳定判据判断闭环系统的稳定性,并绘制闭环系统的阶跃响应曲线来验证其稳定性。(N同题1)
三,实践要求1、根据内容要求,写出的MATLAB程序,及对应的结果、曲线等。
2、实验中需要判定系统稳定性及性能分析的,需要给出理由。
四、结果
1.
a) 程序代码
s=tf('s')G=(s+135/100)/(4*s^3+3*s^2+2*s) %系统开环传递函数 bode(G) %系统Bode图 margin(G) %带有裕度的Bode图 [Gm,Pm]=margin(G) %幅值裕度,相角裕度
复制代码幅值裕度(Gm),相角裕度(Pm)分别是

b) 程序运行结果
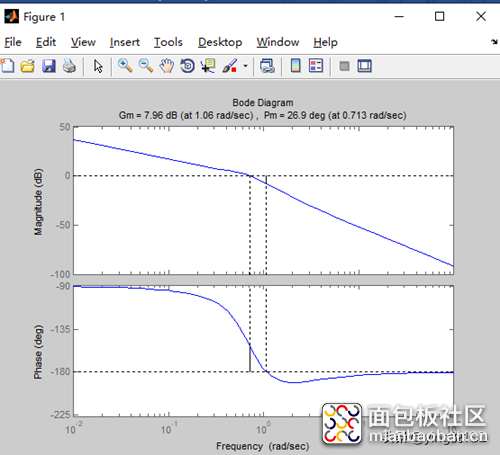
分析:从上图可以看出,开环传递函数,幅值裕度Gm>0,相角裕度Pm>0,所以系统是稳定的。
2.
a)
程序代码
num=135/10;den=[0.1 1.001 0.01 0] G=tf(num,den) figure(1); margin(G) %绘制系统的Bode图 figure(2); nyquist(G) %绘制系统的奈奎斯特图 w=logspace(-1,2,100); %给定频率范围 figure(3); nichols(num,den,w); %绘制系统的尼尔科斯图 ngrid;
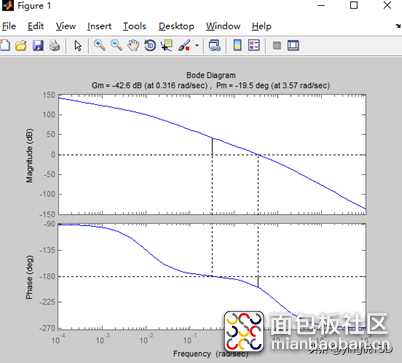
复制代码b) 波特图
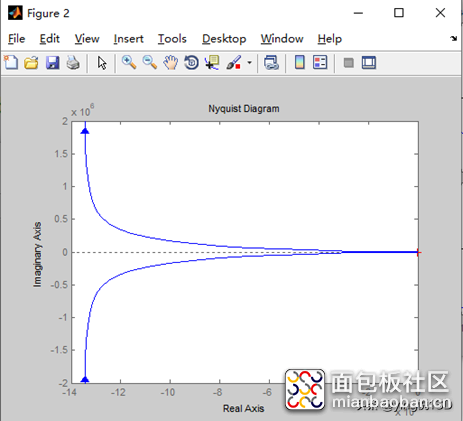
奈奎斯特图
c) 尼尔科斯图
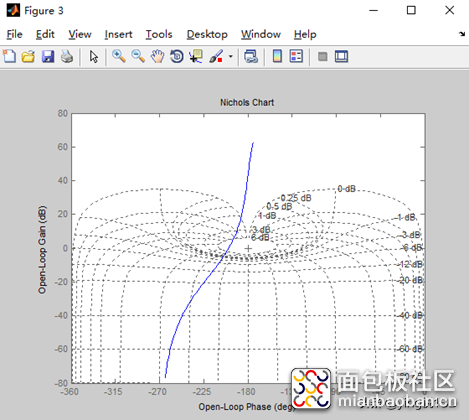
分析::从上图可以看出,开环传递函数,幅值裕度Gm<0,相角裕度Pm<0,所以系统是稳定的。
3.
a)
程序代码
num=[12 4*1.35];den=[2 1 0]; G=tf(num,den) figure(1); nyquist(G) %绘制系统的nyquist图 figure(2); step(feedback(G,1))%绘制系统的阶跃响应曲线 figure(3);
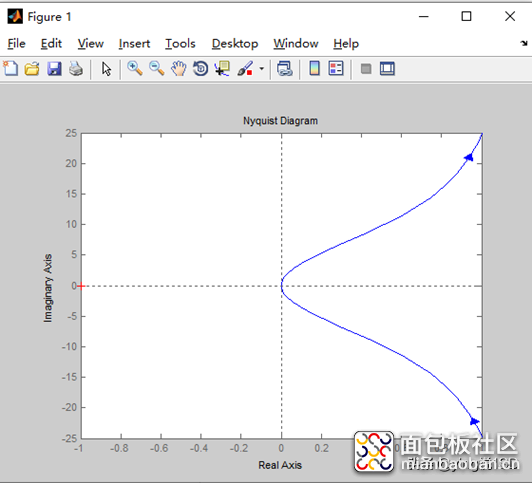
复制代码b) nyquist图
c) 系统的阶跃响应曲线
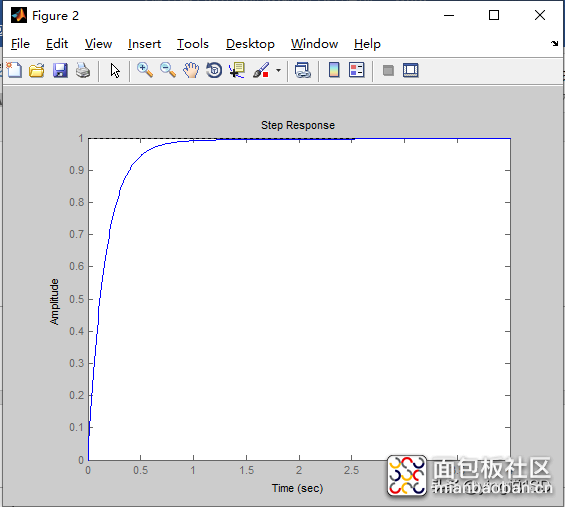
d) 分析:从上图中可以看出,开环系统nyquist图,不包围(-1,j0)点,且开环系统,可以判断,系统是稳定的。







 /2
/2 

