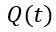
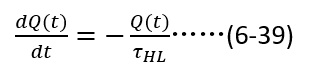
需要注意的是,在求解(6-39)的过程中,不能直接将(6-38)作为初始值,因为在关断的一瞬间,沟道电流的突然消失,即上一节中
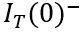
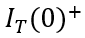
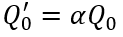
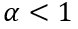
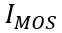
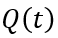
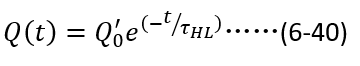
例如,
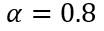
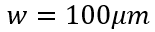
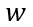
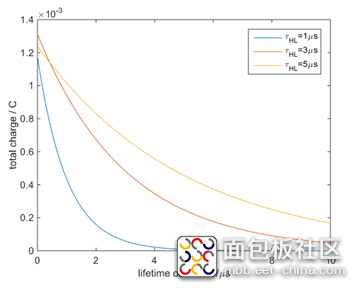
显然,随着载流子寿命的减少,电荷衰减速度加快。因为电流表征了电荷随时间的变化率(电荷的时间微分),利用(6-39)和(6-40),乘以系数
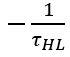
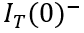
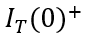
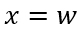
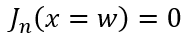
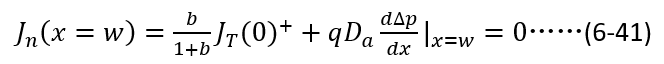
此时多余载流子空穴的分布不变,参考(6-10),
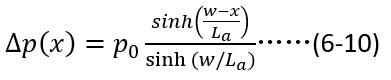
可以计算得到(6-41)第二项的微分表达式,即
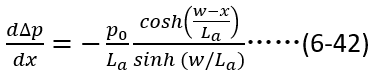
同时,很容易推导双极性扩散长度与空穴扩散长度之间的关系如下(过程省去,读者可以自行推导),
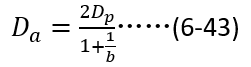
将(6-42)和(6-43)带入(6-41),就可以得到关断瞬间
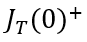
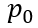
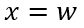
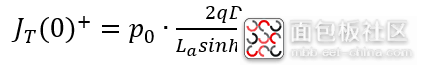
接下来,只需将
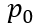
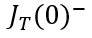
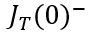
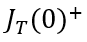
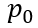
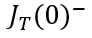
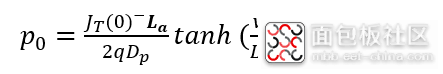
将(6-45)带入(6-44),即得到,
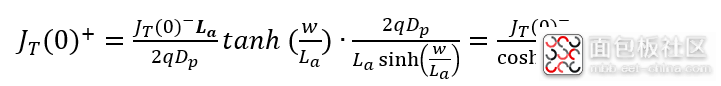
根据(6-46),关断瞬间电流突变的幅度取决于芯片厚度
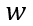
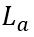
令
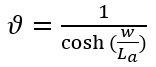
,电流突变率,
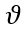
随芯片厚度
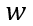
、迁移率
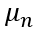
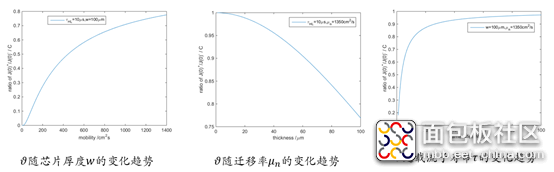
和载流子寿命
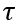
的变化趋势如下图所示:
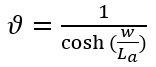
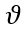
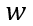
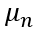
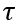
在稳态部分的分析中,我们详细地推演了电子电流、空穴电流、总电流以及各电压构成部分与多余载流子浓度分布之间的关系,即一维空间的物理关系。接下来,我们引入时间变量
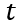
,进入瞬态部分的分析。当外部栅极控制电压
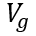
降低到阈值电压
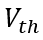
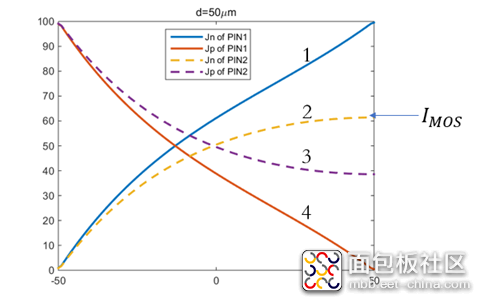
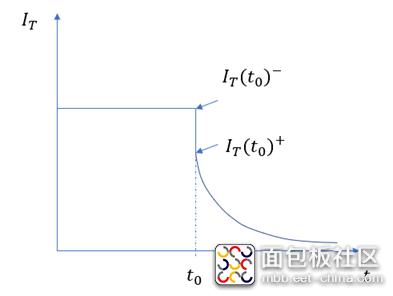
以下时,MOS部分的沟道立即闸断,相应的电子电流变为0,借鉴《电流与电荷分布的初步分析1》中的插图,即图中
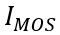
瞬间衰减为0,那么总电流就只剩下如图2、3、4三个部分。假设这个变化的时间为
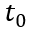
,变化前后的总电流记为
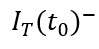
和
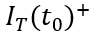
,描绘总电流在时刻发生突变。显然,
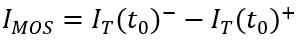
,下一节我们会具体地讨论
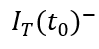
和
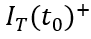
的关系。
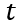
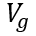
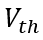
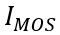
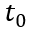
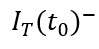
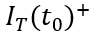
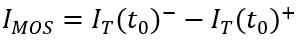
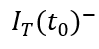
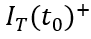
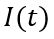
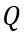
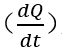
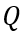
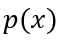
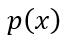
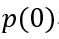
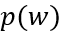
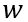
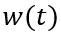
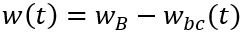
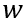
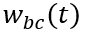
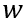
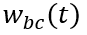
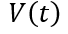
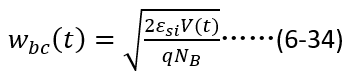
由此,根据稳态部分的边界条件,我们就可以准确地推演出关断瞬态过程中
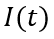
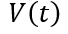
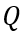
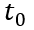
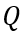
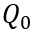
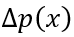
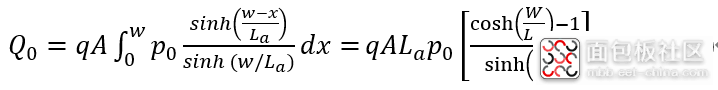
其中,A为芯片面积。分子利用
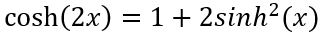
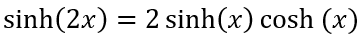
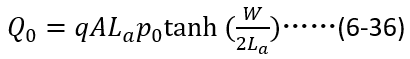
接下来,我们建立
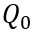
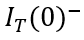
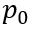
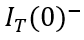
在稳态分析中,我们分别基于PIN模型和BJT模型建立了
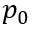
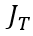
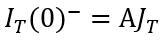
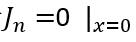
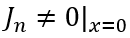
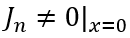
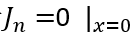
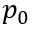
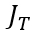
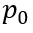
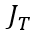
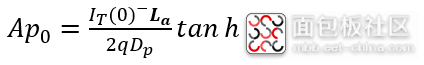
将(6-37)带入(6-36),即可得到
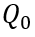
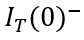
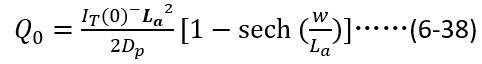
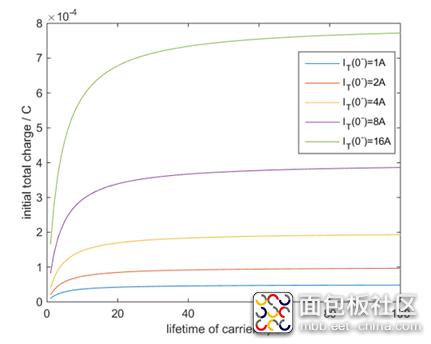
根据(6-38),我们看看初始电荷总量随稳态电流以及载流子寿命之间的变化关系。显然,在稳态电流值确定的情况下,初始电荷总量随载流子寿命增加而趋向饱和。







 /1
/1 
