随着基于模型设计的广泛应用，模型在环仿真也逐渐多了起来，我们今天介绍几种嵌入式常用滤波算法的matlab实现。

一、采用数字滤波算法克服随机干扰的误差具有以下优点：


  • 数字滤波无需其他的硬件成本，只用一个计算过程，可靠性高，不存在阻抗匹配问题。尤其是数字滤波可以对频率很低的信号进行滤波，这是模拟滤波器做不到的。
  • 数字滤波使用软件算法实现，多输入通道可共用一个滤波程序，降低系统开支。
  • 只要适当改变滤波器的滤波程序或运算，就能方便地改变其滤波特性，这对于滤除低频干扰和随机信号会有较大的效果。
  • 在单片机系统中常用的滤波算法有限幅滤波法、中值滤波法、算术平均滤波法、加权平均滤波法、滑动平均滤波等。
%% 代码测试框架 clear signal=wgn(1,1000,10); signal=10+signal; signalFited=zeros(1,1000); for i=1:1000 signalFited(i)=MyFilter(@LowPasFilter,signal(i)); % 改一下句柄名字就可以了。 end plot(signal); hold on; plot(signalFited); function output = MyFilter(fun,input) %MyFilter 滤波测试函数 % MyFilter.m output=fun(input); end

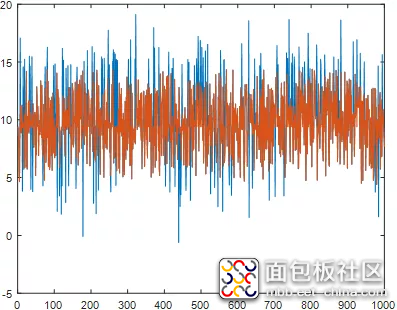
二、限幅滤波

该运算的过程中将两次相邻的采样相减，求出其增量，然后将增量的绝对值，与两次采样允许的最大差值maxErr进行比较。maxErr的大小由被测对象的具体情况而定，如果小于或等于允许的最大差值，则本次采样有效;否则取上次采样值作为本次数据的样本。
限幅滤波法主要用于处理变化较为缓慢的数据，如温度、物体的位置等。使用时，关键要选取合适的门限制maxErr。通常这可由经验数据获得，必要时可通过实验得到。
function out = LimRanFilter(input) %LimRan 限幅度滤波函数 % LimRanFilter.m maxErr=5;%允许最大误差 persistent last; if isempty(last) last=input; end%上一次的值 if((input-last)>maxErr||(last-input)>maxErr) out=last; else out=input; end end
up-7317ba0a0b3939307eb5e161cf874bb481e.png

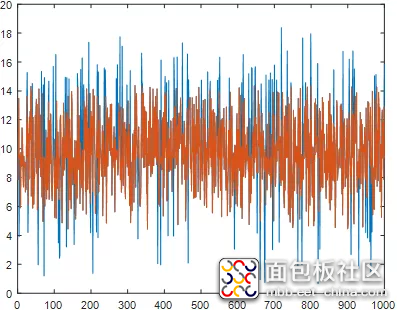
三、中值滤波

该运算的过程是对某一参数连续采样N次(N一般为奇数)，然后把N次采样的值按从小到大排列，再取中间值作为本次采样值，整个过程实际上是一个序列排序的过程。
中值滤波比较适用于去掉由偶然因素引起的波动和采样器不稳定而引起的脉动干扰。若被测量值变化比较慢，采用中值滤波法效果会比较好，但如果数据变化比较快，则不宜采用此方法。
function output= MeanFilter(input) %MeanFilter 中值滤波 % MeanFilter.m persistent buff; if isempty(buff) buff=[2 0 0 0 0 0]; end%选择序列 if(buff(1)<7) buff(buff(1))=input; buff(buff(1))=buff(buff(1))+1; else for i=2:5 if(buff(i)>buff(i+1)) temp=buff(i); buff(i)=buff(i+1); buff(i+1)=temp; end end buff(2:6)=0; buff(1)=2; end%初始化滤波缓冲区 output=buff(4); end
up-f859cca48e3eef9f4224ebe59630fa828eb.png

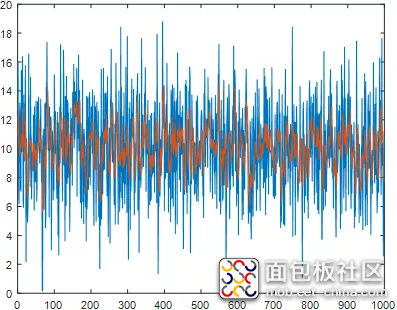
四、滑动平均滤波

平均滤波算法有一个特点，即每获取一个有效采样值必须连续进行若干次采样，当采速度慢时，系统的实时得不到保证。这里介绍的滑动平均滤波算法只采样一次，将一次采样值和过去的若干次采样值一起求平均，得到的有效采样值即可投入使用。如果取N个采样值求平均，存储区中必须开辟N个数据的暂存区。每新采集一个数据便存入暂存区中，同时去掉一个最老数据，保存这N个数据始终是最新更新的数据。采用环型队列结构可以方便地实现这种数据存放方式。
function output= MovAveFilter(input) %MovAveFilter 滑动平均滤波 % ´MovAveFilter.m persistent buff; if isempty(buff) buff=[ 0 0 0 0 0 ]; end%滑动窗口 persistent numOfBuff; if isempty(numOfBuff) numOfBuff=0; end%´当前窗口元素 persistent k; if isempty(k) k=1; end%计数器 buff(k)=input; k=mod((k+1),5)+1; numOfBuff=numOfBuff+1; if(numOfBuff>5) numOfBuff=5; end output=sum(buff)/numOfBuff; end
up-63c2814335b685da5f09e2604deefbda9df.png

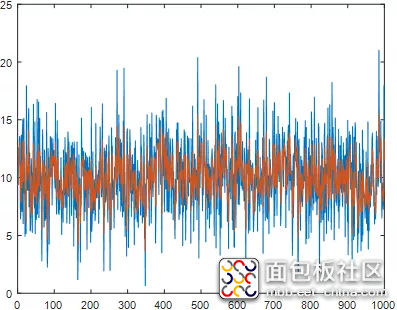
五、低通滤波

将普通硬件RC低通滤波器的微分方程用差分方程来表求，变可以采用软件算法来模拟硬件滤波的功能，经推导，低通滤波算法如下：
Yn=a* Xn+(1-a) *Yn-1 式中 Xn——本次采样值 Yn-1——上次的滤波输出值; a——滤波系数，其值通常远小于1; Yn——本次滤波的输出值。
function output= LowPasFilter(input) %LowPasFilter低通滤波 % ´LowPasFilter.m persistent yn0; if isempty(yn0) yn0=0; end%上次输出值 a=0.5;%滤波系数 output=inputa+yn0(1-a); yn0=output; end
up-b38f158ab2766ef5f22aa2a17273a7a8bd7.png
这几种是使用较多的滤波算法，比较方便进行仿真与编写，还有扩展卡尔曼等的实现可以根据实际情况来运用，在一般领域这几种滤波算法已经能够达到很好的效果了。

来源：https://my.oschina.net/u/4219848/blog/5269820 阿木社区