首先需要明白的是振荡电路的设计原理。
原理如下所示:
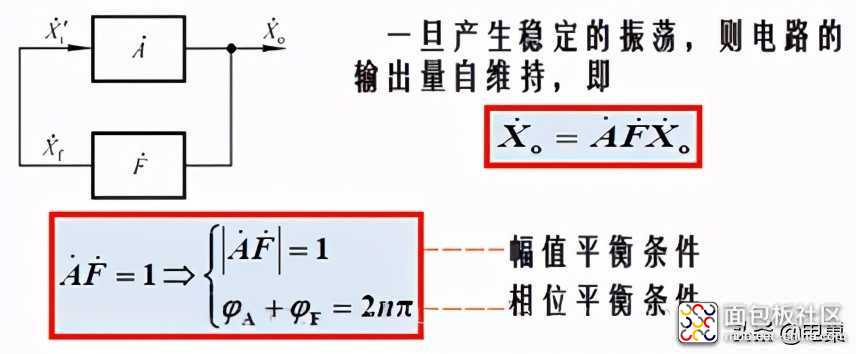
要产生正弦波振荡,必须有满足相位条件的f0,且在合闸通电时对于f= f0信号有从小到大直至稳幅的过程,即满足起振条件。
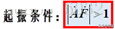
RC串并联选频网络:
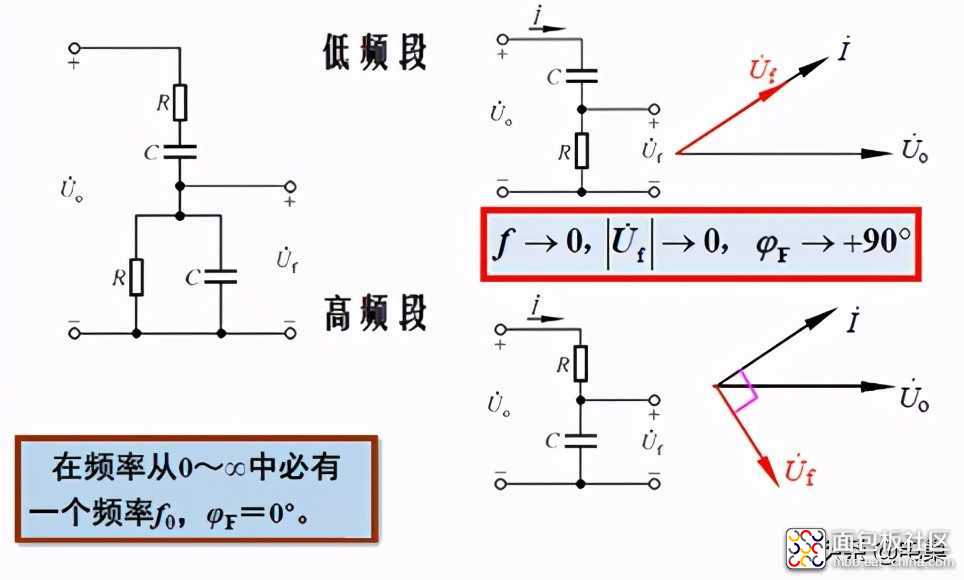
下面求出电路的频率特性:
首先介绍最简单常见的文氏桥振荡电路
振荡电路设计原理如下:
特点:以RC串并联网络为选频网络和正反馈网络,并引入电压串联负反馈,两个网络构成桥路,一对顶点作为输出电压,一对顶点作为放大电路的净输入电压,就构成文氏桥振荡电路。
仿真电路见右图所示:
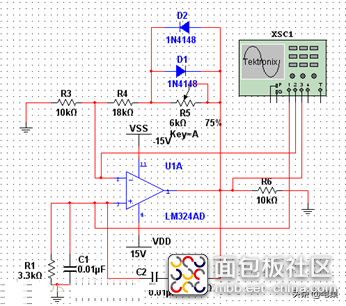
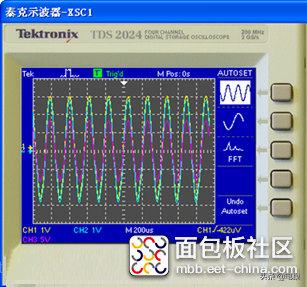
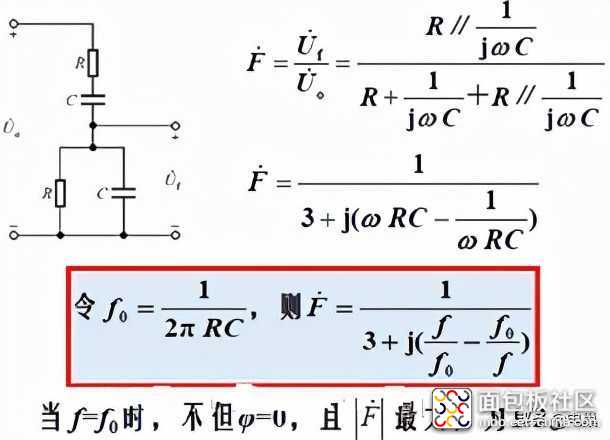
说明:振荡频率由求得。
而调节R5电阻可以调节正弦波的输出幅值。
两个二极管是用来稳定输出电压的。
在开始时,为了使电路起振,所以使正反馈的作用大于负反馈,在达到需要的幅值之后,就使正负反馈的作用相同。
下面来看另外一个例子:
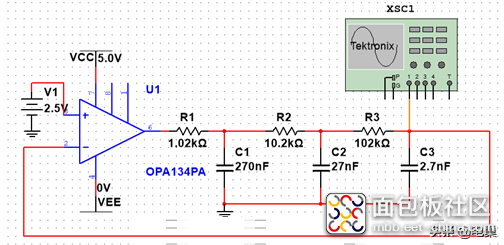
根据振荡电路的设计要求,要想完成振荡必须首先满足相位条件。
图中有三个低通滤波器,每个都可以提供相移。
可以看出三个低通滤波器的时间常数一样,因此他们提供的相依理论上是一样的。
电路输出信号直接反馈到运放的反向输入引脚,因此此处会引入-180°的相移。
而对于三个低通滤波器网络引入的相移范围为0°至-270°。
因此存在一个频率使得整体相移为-360°,满足相位条件。
也就是说每个低通滤波器引入的相移是-60°,因此可以知道频率的计算公式如下:
F = tan 60 degrees / 2 * pi * R1 * C1
F(s)=1/(1+jwRC)的相角为-60°,也就是上面的公式。
为了是信号能够在单电源下工作,可以引入直流偏置,直接分析直流通路,可以看书,输出信号中会叠加出来2.5V的直流信号。
输出幅值由于衰减正常比较小,因此可以在后级添加同相放大电路,这样可以将信号进行放大。
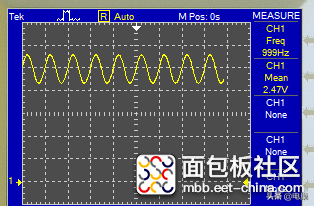
输出的波形如下所示:
方波发生器:
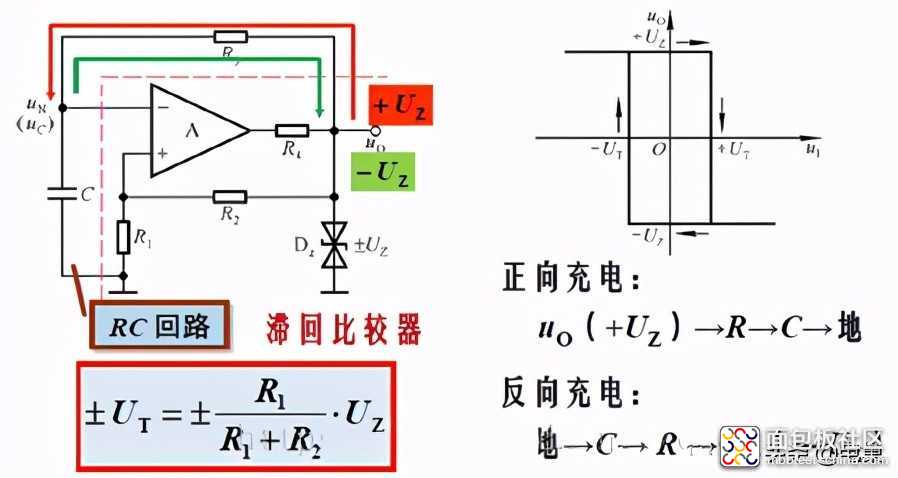
上面的是方波发生器的基本原理,同时具有两路反馈信号,通过两路信号的信号延迟来输出方波。
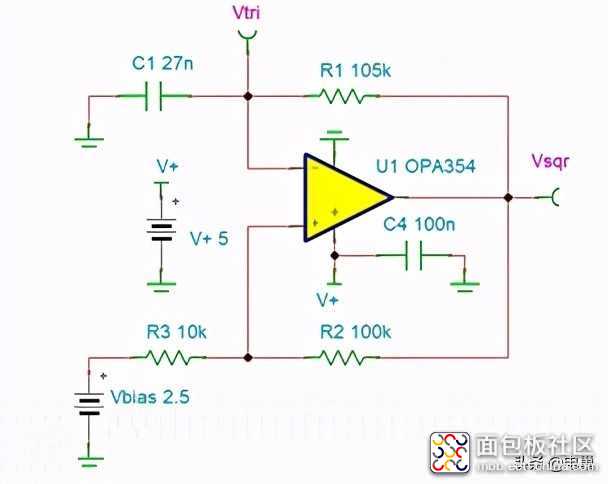
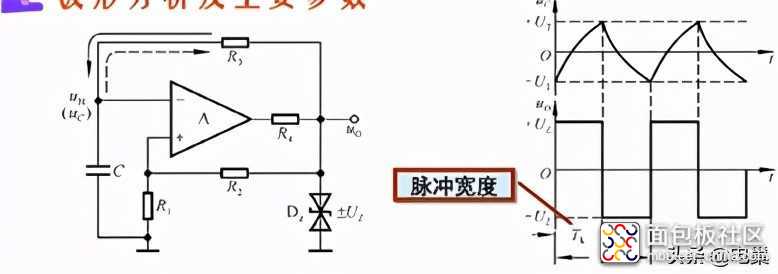
具体的图如左边所示。这里加上限幅器比较好。
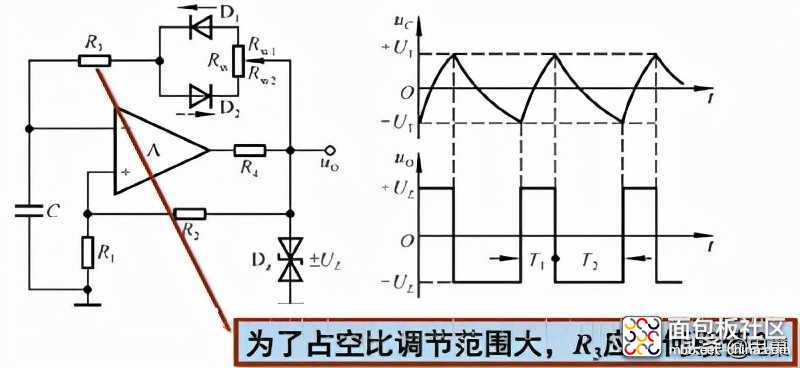
为了使占空比可调只要改变两边的充电时间即可。
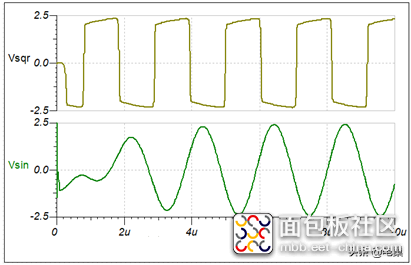
同样由于方波是由无数个正弦波叠加生成的,因此如果使用低通滤波器将信号中的二次以上的谐波滤掉,至保留基波,这样就转变成了正弦波信号。具体信号如下所示:
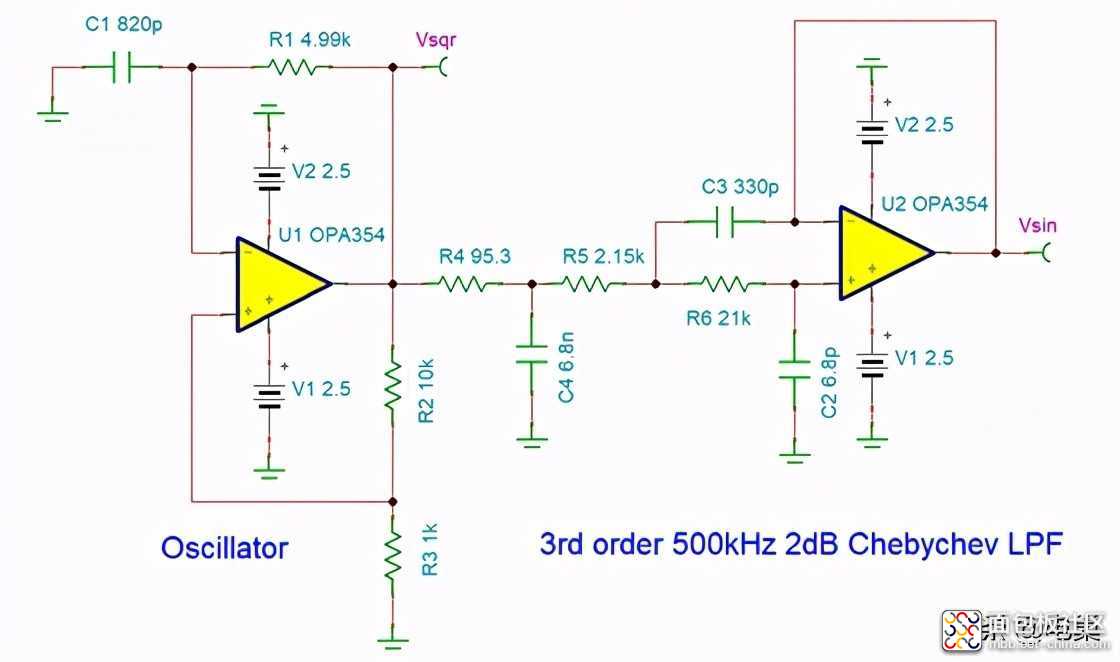
U1生成一个500kHz方波输出,U2形成3阶切比雪夫滤波器,用来滤除高频信号。
输出波形如下所示:
三角波发生电路:
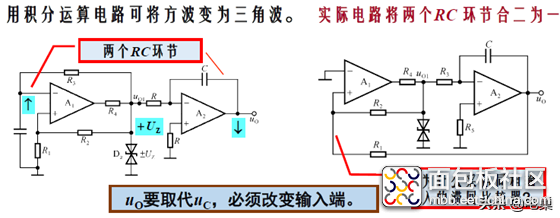
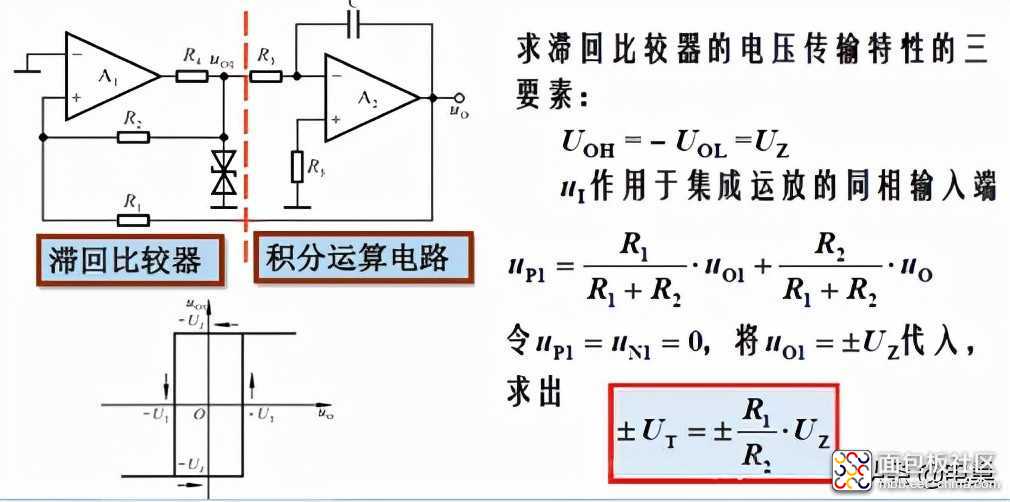
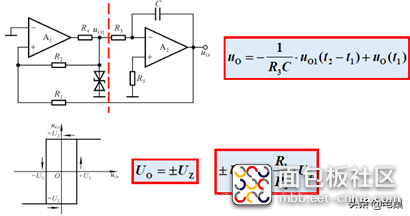
为什么要改变输入方向呢,原因是当第一级输出高电平时,积分电路的输出电压是在往下降的,具体可以列出方程就知道了。
这样,如果第二级的输出电压还反馈到第一级的反向输入端,会导致无法正常工作,因此只能反馈到正向输入端,这样使用叠加原理,可以得出波形。
具体的仿真电路如下所示:
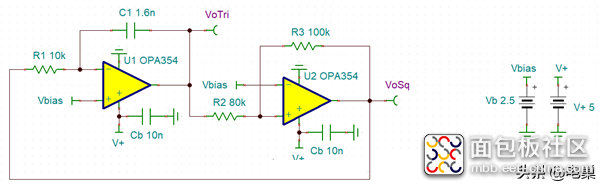
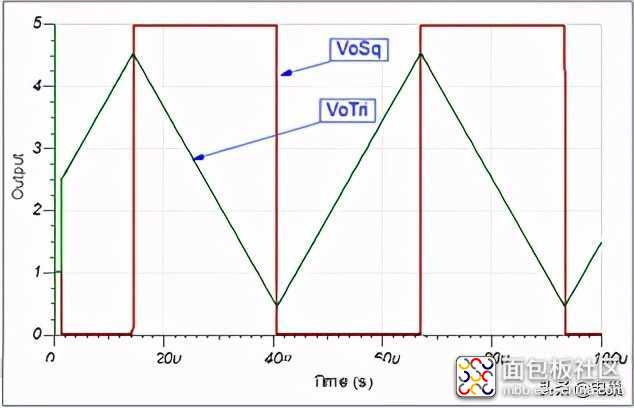
仿真波形如下所示:
振荡频率取决于R1,C1,和U1的峰值-峰值输出.
『本文转载自网络,版权归原作者所有,如有侵权请联系删除』







 /5
/5 

