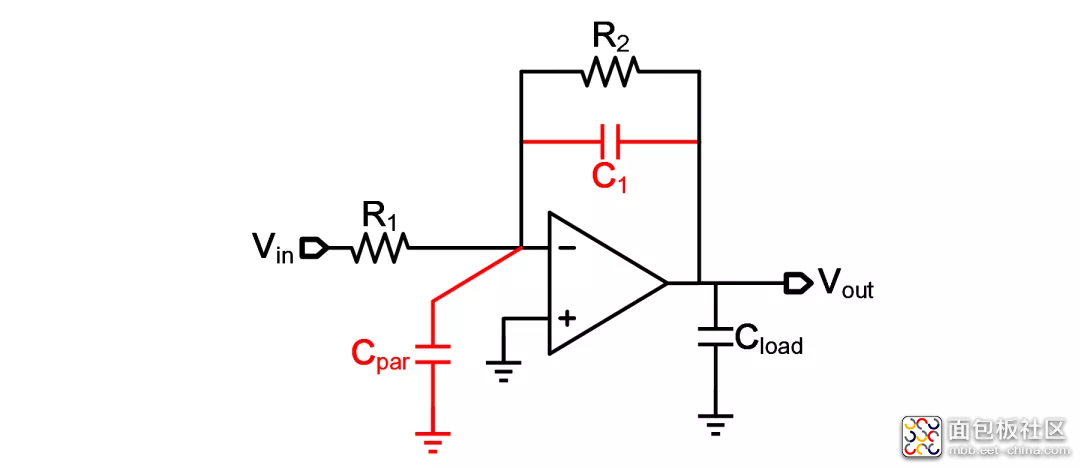
在电阻型放大电路中,如PGA,LDO等,常常会出现如下稳定性问题:单独仿真的稳定性很好的运放接入电阻反馈网络后环路稳定性变差很多。
如图1所示,这是因为将运放接为环路后,运放输入端的寄生电容Cpar也出现在环路中。我们在单仿真运放考虑稳定性时,假设电阻反馈网络是一个简单的比例系数,是频率无关的,因此只考虑运放的零极点对稳定性的影响。而实际客观存在的Cpar使得电阻反馈网络变得频率相关,会引入额外的极点,因此可能恶化环路的稳定性。
笔者在阅读论文和借鉴别人设计的电路时,发现他们常常会在图1中反馈电阻R2上并联一个电容C1来提高稳定性,而通过仿真发现这样确实是很有效的。为了避免做Spice Monkey,本文对这个方法的原理进行简单的分析。
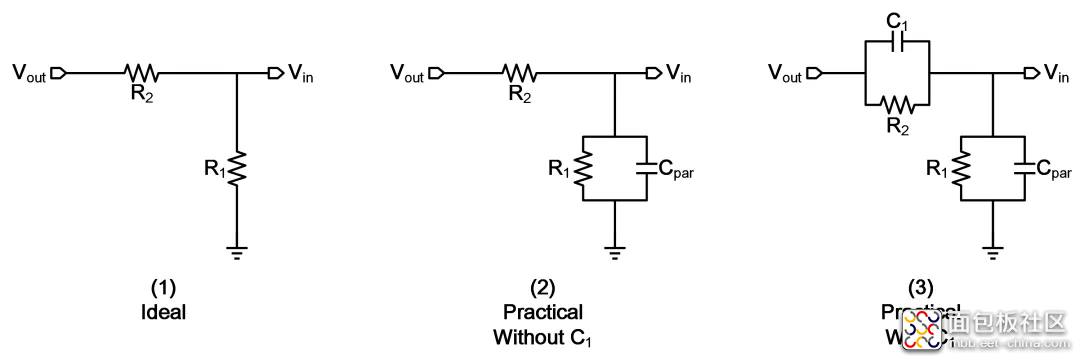
如图2所示,在理想情况下,即不考虑运放输入寄生电容时,如图2(1),电阻反馈网络的频响为式(1):
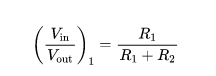
此时电阻反馈网络频率响应仅为一个简单的比例系数,不存在零极点。
考虑实际情况下运放输入端的寄生电容Cpar后,如图2(2),电阻反馈网络的频响为式(2):
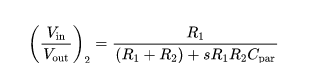
此时电阻反馈网络频率响应和频率相关,且引入一个极点表示为式(3):
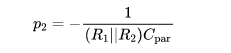
该极点是因为在Vin处同时存在电阻和电容,同时其值也符合Vin处总电容和总电阻之积的速算方法。引入该极点后,整个反馈系统多了一个额外的极点,因此可能存在稳定性恶化的问题。
给R2并联电容C1后,如图2(3),电阻反馈网络的频响为式(4):
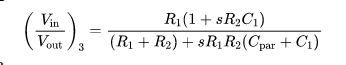
此时极点变为式(5):
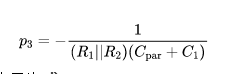
同时还多了一个零点,表示为式(6):
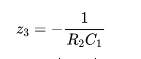
零点的出现是因为从Vout至Vin出现了两条通路—R2通路和C1通路。
并联电容C1后,系统中额外的极点仍然存在(虽然数值发生了变化),但是额外引入了一个零点。通过合理地设计,可以通过这个零点补偿运放输入寄生电容引入的极点带来的相位变化,防止反馈系统稳定性的恶化。







 /2
/2 
