四臂结构是直流电桥的基本形式。电桥由直流电源供电,平衡时,相邻两桥臂电阻的比值等于另外两相邻桥臂电阻的比值。若一对相邻桥臂分别为标准电阻器和被测电阻器,它们的电阻有一定的比值,则为使电桥平衡,另一对相邻桥臂的电阻必须有相同的比值。根据这一比值和标准电阻器的电阻值可求得被测电阻器的电阻值。平衡时的测量结果与电桥电源的电压大小无关。
先来看看平衡直流电桥的计算方法,如下图,在VA=VB的情况下,求电阻Rx的值。
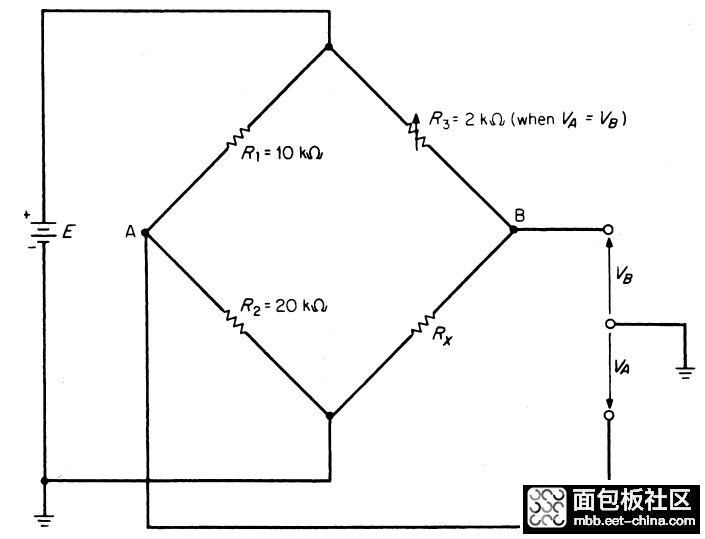
这个就是个直流平衡电桥的电路,也称为惠斯登电桥,用来精确测量1ohm到1Mohm的电阻。这个电桥不平衡的时候,A点和B点有一个潜在的压差,就会有电流流过接在这两个的元素。
来解一下解一下这个电路,调整R3使这个电路平衡以后,Va = Vb。那么就有:
R1/R2 = R3/Rx
把电阻带入,借出来可得到Rx为4Kohm。
再来看一个非平衡电桥的电路,如下图,求Reqt的电阻。
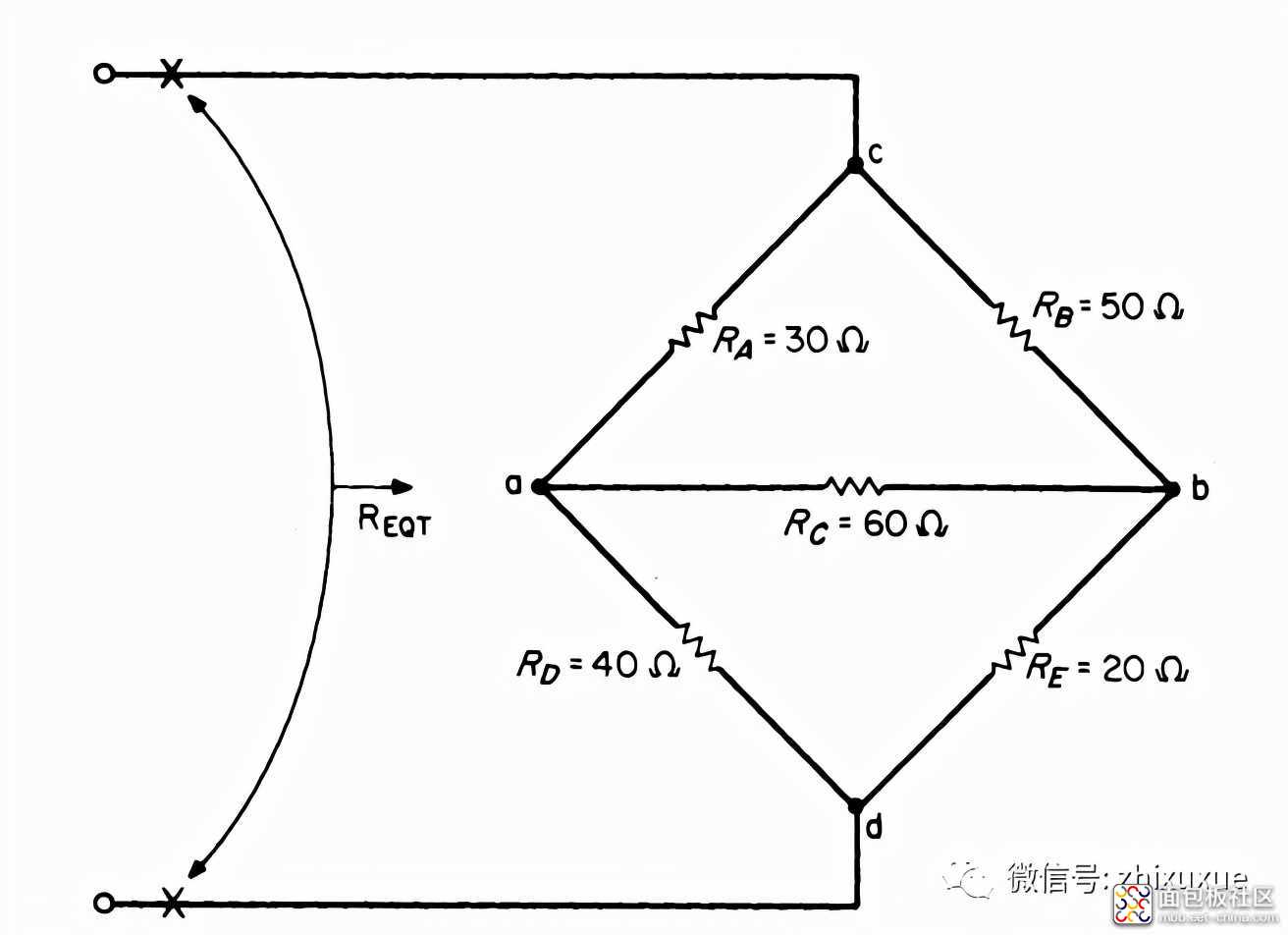
利用星-三角(Delta-Wye)方法比较容易化简这个电阻,这里简单介绍一下星-三角的公式,下图a是星形电路,b是三角形电路,c是星到三角的变化。
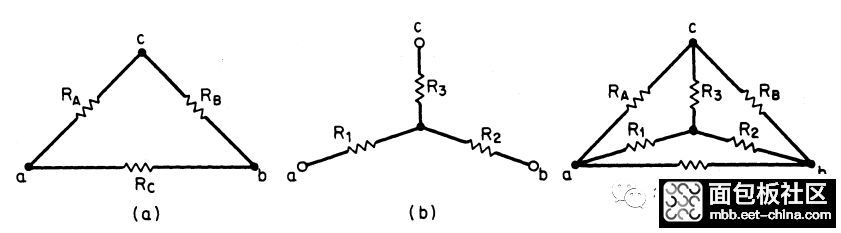
三角形到星形变换(delta-to-wye):
R1 = RARC/(RA + RB + RC)
R2 = RBRC/(RA + RB + RC)
R3 = RBRA/(RA + RB + RC).
星形到三角形变换(wye-to-delta)
RA = (R1R2 + R1R3 + R2R3)/R2
RB = (R1R2 + R1R3 + R2R3)/R1
RC = (R1R2 +R1R3 + R2R3)/R3
知道了这个公式,那么上面的电路图就可以直接根据公式进行三角形到星形的化简了。
只需要把,RA = 30, RB = 50, RC = 60,代入公式,就可以求出来等效星形电路下的电阻R1,R2和R3。
R1 = 12.9, R2 = 21.4, R3 = 10.7。
那么原图形就变成了下面的图形了。图a是三角到星形的变化示意图,b是根据结算,等效以后结果。
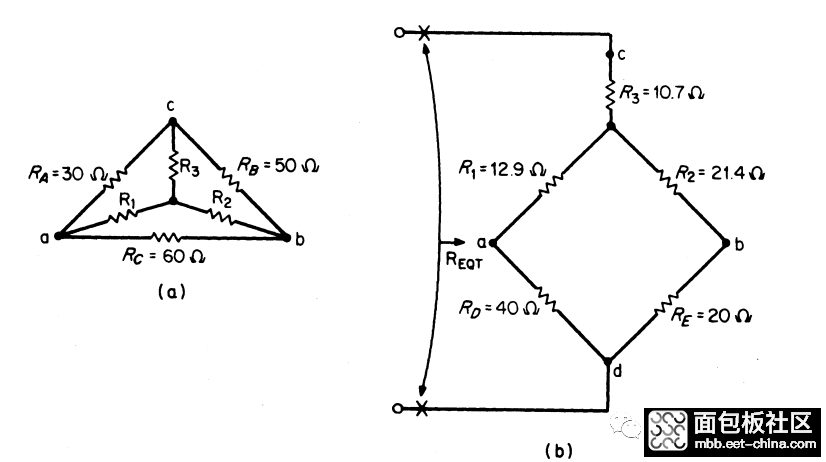
电路化成b以后,就是变成了基本的串并联电路了,求REQ就很简单了。
REQ = R3+(R1+RD)||(R2+RE)
代入相对应的数值,就可以求出来REQ的值为33.9ohm。
该内容是小编转载自山汛札记,仅供学习交流使用,如有侵权,请联系删除。






 /5
/5 

