前几天,我通过一顿傅里叶级数展开的生猛操作,在频率域上,深入透彻地分析了PWM信号的谐波幅度以及滤波电路的设计。
但是,事情还没有结束。
对于模拟量输出信号,还需要考虑其输出电流的响应时间。
以4-20mA信号为例,从处理器调整了PWM信号占空比开始计时,至4-20mA的电流调整至该 占空比对应电流结束计时,所得到的时间即为响应时间。
响应时间太长,可能导致对4-20mA所接设备的调节速度不够,使得设备无法响应其负载变化。
甚至可能在检测到故障之后,因为响应时间太长,无法及时关闭设备而导致严重的后果。
我们需要在时域对PWM信号的滤波电路做瞬态分析。
一阶R、C滤波电路的时序分析
以下图所示的一阶R、C低通滤波电路为例,
PWM信号的频率为1.5kHz,占空比为50%,高电平为U。
R1=100kΩ,C1=6.8uF,
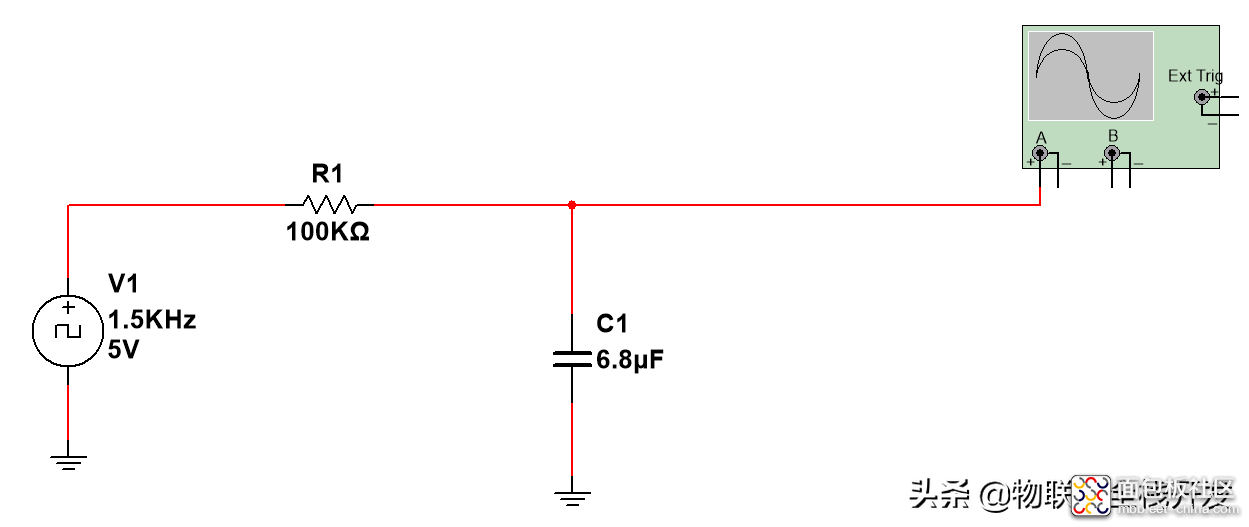
一阶R、C低通滤波电路
当PWM信号输入到该电路时,在PWM信号的高电平输出期间,高电平通过R1向C1充电。
在低电平输出期间,C1通电R1向低电平放电。
其波形如下图所示:
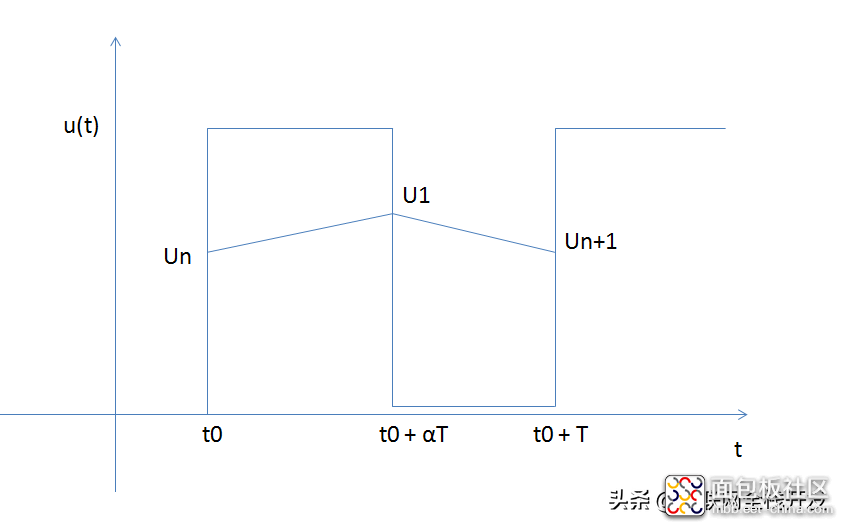
PWM信号的充放电波形
在高电平期间,
以t0为0时刻,
该电路的三要素为:
时间常数
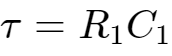
,
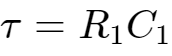
0时刻的电压
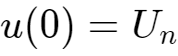
,
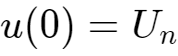
时间无限长之后的电压
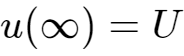
,
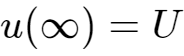
该电路的一阶微分方程,求得电容两端电压的通解为:
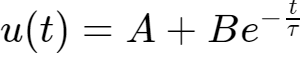
根据
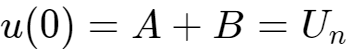
,以及
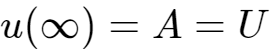
,
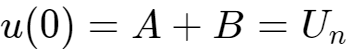
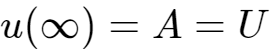
得到
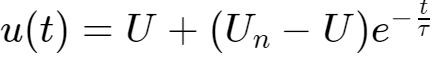
,
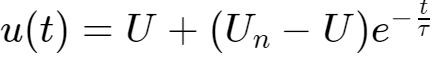
在
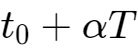
时刻,有
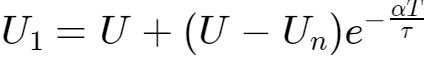
,(式1)。
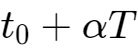
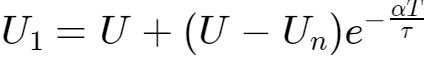
在低电平时刻,
以
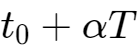
为零时刻,
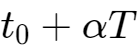
该电路的三要素为:
时间常数
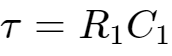
,
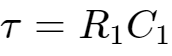
0时刻的电压
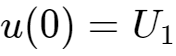
,
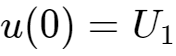
时间无限长之后的电压
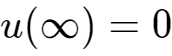
,
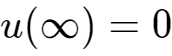
该电路的一阶微分方程,求得电容两端电压的通解为:
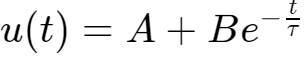
根据
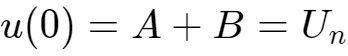
,以及
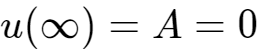
,
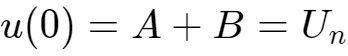
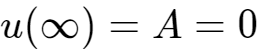
得到
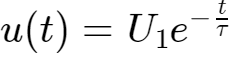
,
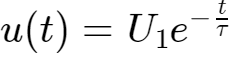
在
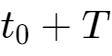
时刻,有
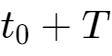
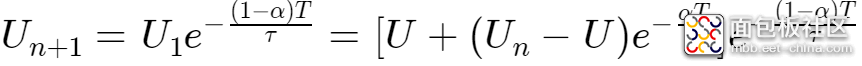
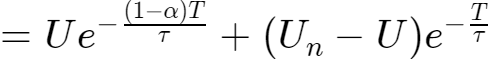
泰勒级数展开分析
指数函数
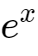
的泰勒级数展开式为:
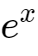
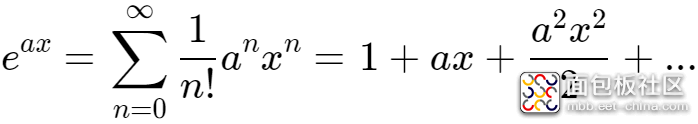
当
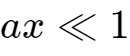
时,舍去二阶小量,有
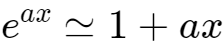
,所以有:
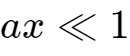
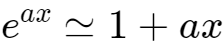
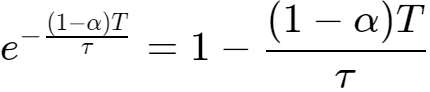
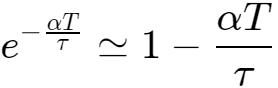
代入式2,得到:
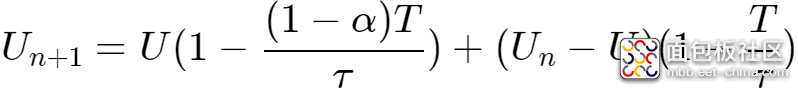
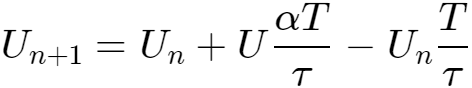
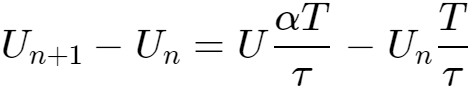
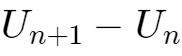
当
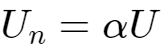
时,增量为0,
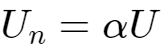
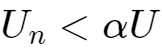
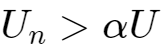
所以最终电压会在
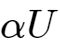
附近反复充放电。
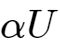
进一步移项变形得到:
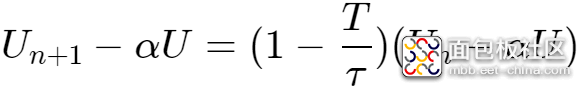
记
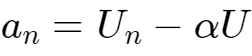
,得到,
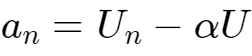
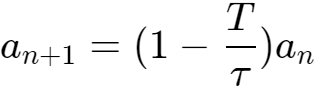
这是等比数列,得到:
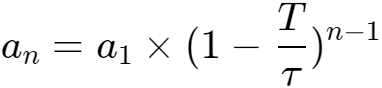
如果开始时电容电压为0,得到:
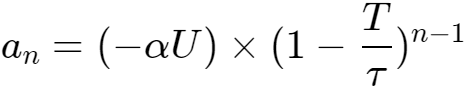
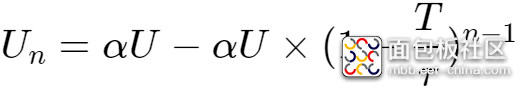
因为
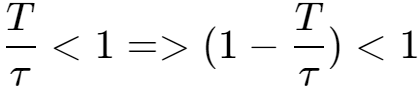
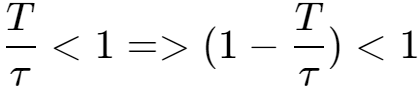
所以,当n趋于无穷时,
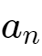
趋近于0,即
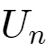
趋近于
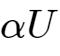
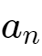
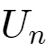
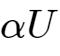
即最终达到
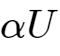
的电压。
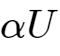
响应时间分析
当
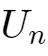
与目标电压
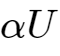
的相对误差小于0.1%即认为达到了目标电压。
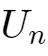
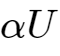
得到:
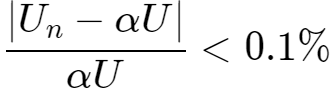
得到:
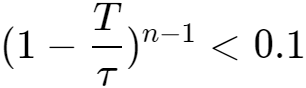
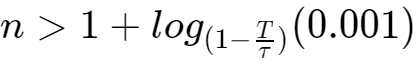
当
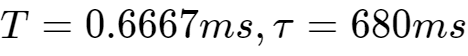
时,算出n>7043.
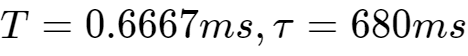
对应时间为:
t>15235*0.6667ms=4.7s。
即至少要10s之后,4-20mA的电流与目标值的误差才能小于0.1%。
根据式1得到,纹波为:
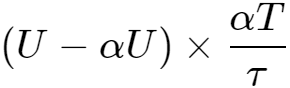
纹波系数为:
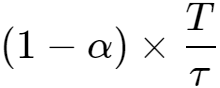
当占空比为50%,频率为1.5kHz时,如果纹波系数需要小于0.1%,得到:
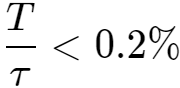
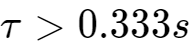
当
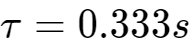
时,误差小于0.1%的响应时间为2.3s。
Multisim仿真验证
Multisim仿真验证
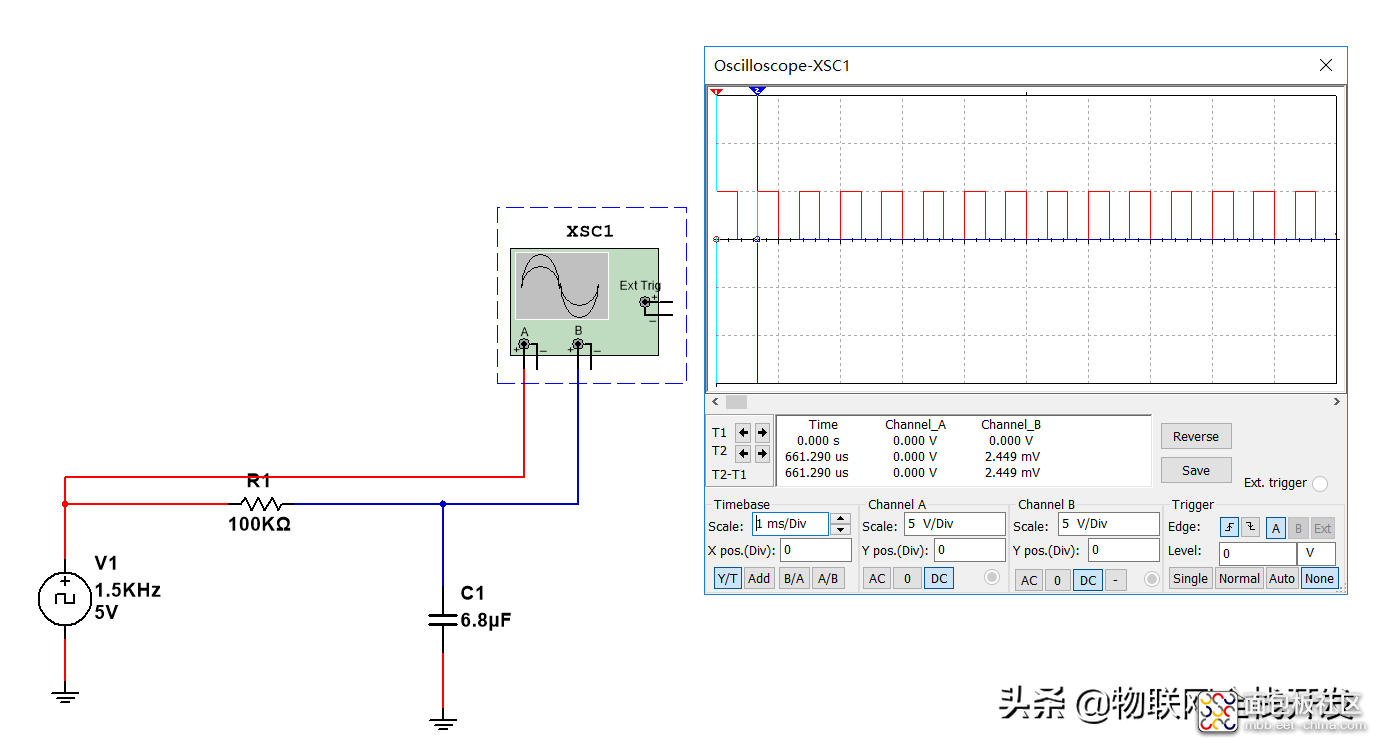
将本文推导得到的式3的计算结果与multisum的测试结果进行比较,结果完全一致,验证了公式的正确性。
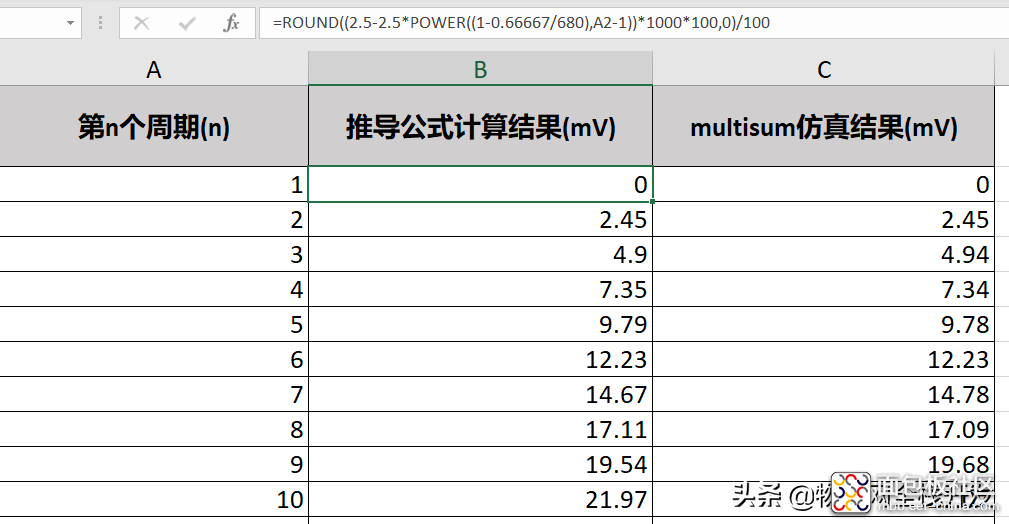
结果比对
而电容两端电压从0V上升到2.5*(1-0.1%)=2.4975V所耗费的时间为4.76s,
这与理论计算的4.7s也完全一致。
说明了本文对响应时间评估的正确性。
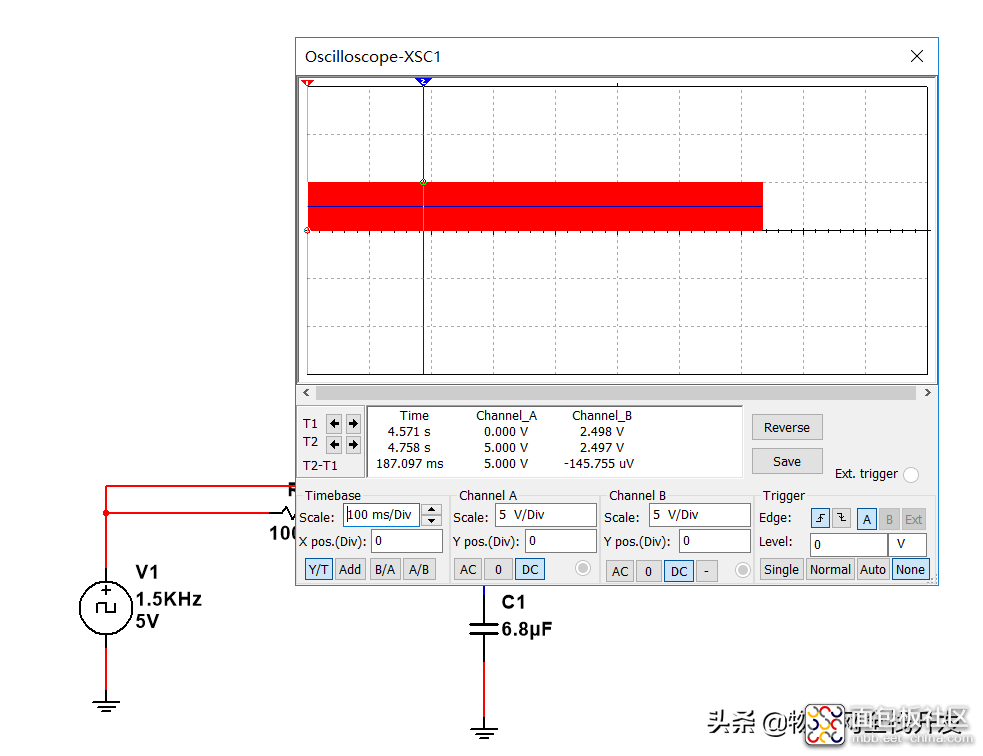
响应时间测量
结束
当采用一阶R、C滤波电路对PWM进行DAC转换时,可以采用泰勒级数展开得到解析解。
由该解析解,根据实际的纹波系数,响应时间等规格,选择合适的PWM频率、电阻阻值、电容容量等参数。
来源:物联网全栈开发






 /1
/1 

