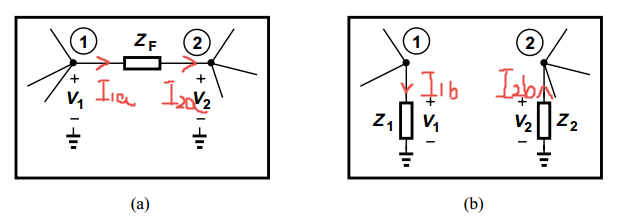
什么是米勒定理？如下图(a)所示，如果在结点1和结点2之间存在一阻抗ZF，则可以把ZF变换成两个到地的阻抗Z1和Z2，如图(b)所示。变换过程中，需要保证电路中电流和电压，在变换前后保持不变。具体就是说：(1) 从结点1中流入ZF的电流==从结点1种流入Z1的电流，即I1a=I1b(2) 从ZF流入结点2的电流==从Z2流入结点2的电流，即I2a=I2b。
由I1a=I1b可知，
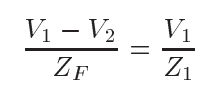由I2a=I2b可知，
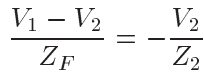设从结点1到结点2的增益为Av, 即Av=V2/V1,则：
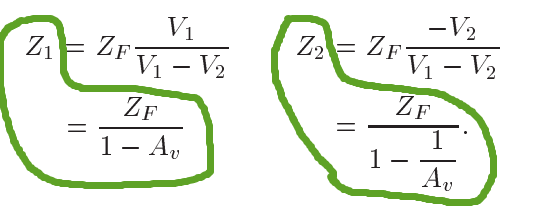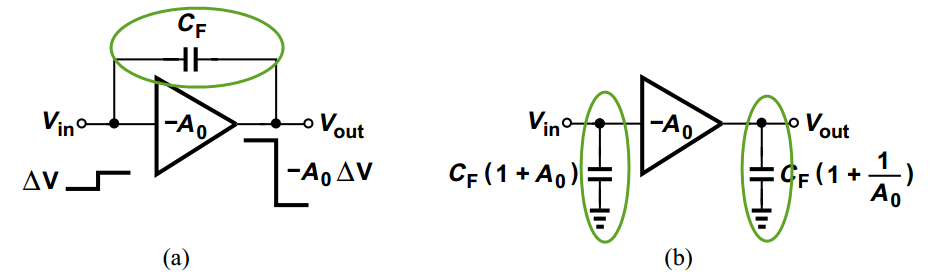
以上即称为"Miller's theorem"。具体表述为：当结点1和结点2之间存在一阻抗ZF，结点1和结点2之间的增益为Av，则可以将ZF变换成对地的阻抗Z1和Z2。怎么用米勒定理进行分析？米勒定理，将连接两个结点1和2的阻抗，变换成对地的阻抗Z1和Z2，可以大大地简化电路分析，可以有助于对电路产生一个直观的认识。比如说，如下图所示，在放大器的输入和输出端，存在一反馈电容，那么这个电容会对放大器的输入和输出阻抗产生什么影响呢？
由米勒定理可知，
也就是说，CF的存在，使得放大器的输入电容变大(1+A0)倍，即该电路输入电容的大小，受到"米勒倍增(Miller Multiplication)"效应的影响。当A0>>1时，输出电容的大小等于CFS。
从以上的分析可知，由于电容CF的米勒效应，会使得放大器的输入电容变大(1-Av)倍。
对于反馈放大器，米勒效应实际上非常有益，因为稳定放大器可能需要一个太大而无法实际包含在电路中的电容器，这通常是电容器消耗大量面积的集成电路的一个问题
米勒近似(Miller approxiamtion)米勒原理中的参数都是频率相关的，其等式要求在同一频率下成立。但是，如果把参数都写成频率相关的话，那想要通过运用Miller原理简化电路分析也就无法实现了，因为这个时候，其复杂度，并不会比直接对电路进行分析来得低。所以，一般都会取放大器的低频增益作为等式中的Av，尽管在高频时，其增益会受到反馈电容CF的影响。另外，米勒效应可能会消除传输函数中的零点。
那米勒效应会有什么影响呢？大多数的放大器是反相的，由于米勒效应，其输入端的有效电容会增加。这会降低放大器的贷款，影响放大器的高频响应特性。也可以利用米勒效应引起的电容倍增效应，由较小的电容器产生较大的电容器。这在IC设计中很重要，因为大容值的电容器会占用大量面积，从而增加成本。
本文由编辑推荐，原出处：https://www.eet-china.com/mp/a148599.html
/2 
