RC电路和RL电路都存在时间常数，它是反应电路随时间衰减，有一个过渡期的时间常数。其中RC电路时间常数：τ＝RC，LR电路时间常数：τ＝L/R。那为什么叫时间常数呢，他和时间又有什么关系呢？首先看RC电路：
当AB两端的直流电源突然断开时，通过AB的电流瞬间中断，但电容两端的电压不会突变（中断前后瞬间不变），所以Uc=UR。此刻存储在C中的能量被释放到电阻R上,由此形成一个串联组合。
9a20ba27965d45d49f381f2f6041e279~noop.image?_iz=58558&from=article.jpg

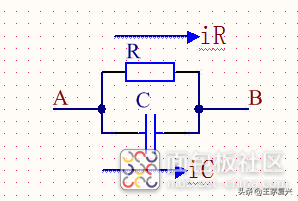
根据节点处的电流（KCL）情况得：需要用到点微积分
e1f5a37c72004caaad1a12f2cd19239f~noop.image?_iz=58558&from=article.jpg

就得到了电容电压随时间衰减的关系式，且是按指数形式衰减。
那么电容电压随时间衰减的速率是：
6986a9b330b440f89e4476dc9b2d9469~noop.image?_iz=58558&from=article.jpg

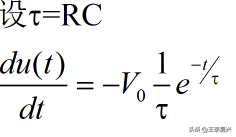
所以t=0时，可到初始电压V0的衰减速率：
343f6226d91d420185d6bf01e65a422c~noop.image?_iz=58558&from=article.jpg

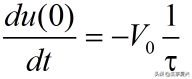
初始电压V0衰减到0需要的时间是：
ef4c843d305f46c6b7329db911507725~noop.image?_iz=58558&from=article.jpg

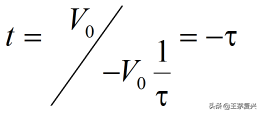
由此得到RC就是初始电压V0以恒定的速率衰减到0所需要的时间。这就是为什么叫做时间常数的原因，公式中负号的意思是电压随时间在衰减。
当t=τ时：可得到
d44adbd846354c8fb72d153794b8ab62~noop.image?_iz=58558&from=article.jpg

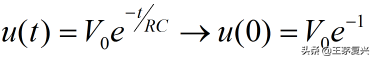
所以时间常数又可表示为电路衰减到初始值的1/e或36.8%所需的时间。时间常数越小，电压降低的越快（衰减速度加快），电路的响应就越快，使得电路迅速达到稳定的状态。
那么除了计算时间常数外还可以用仪器来测定时间常数，原理如下：
首先对衰减指数求导:
35471783b6394437a39a1cbae7dbed98~noop.image?_iz=58558&from=article.jpg

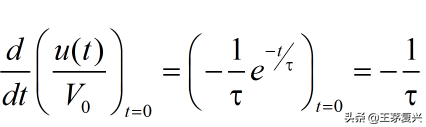
得到初始斜率-1/τ, τ恰好是切线与时间轴相交于t=τ的点，如下图。
514a1f31252d4130b7f1c5c7c0842fe5~noop.image?_iz=58558&from=article.jpg

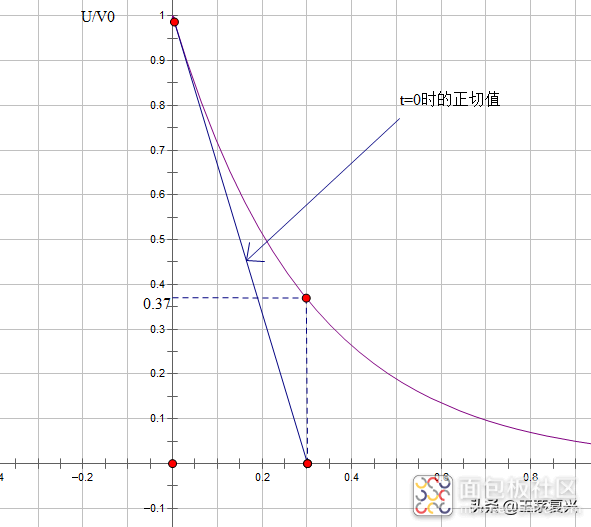
以上就是对RC线路中时间常数的全部解释，RL电路中的时间常数和RC线路分析原理类似，有兴趣的朋友可以自己试着推导下。