看到一个高速电路,两个运放之间有一个阻容并联结构,目的是为了滤波,搭建了一个简单的电路仿真一下,分别用方波作为输入信号源和交流参数扫描,所得结果如下:



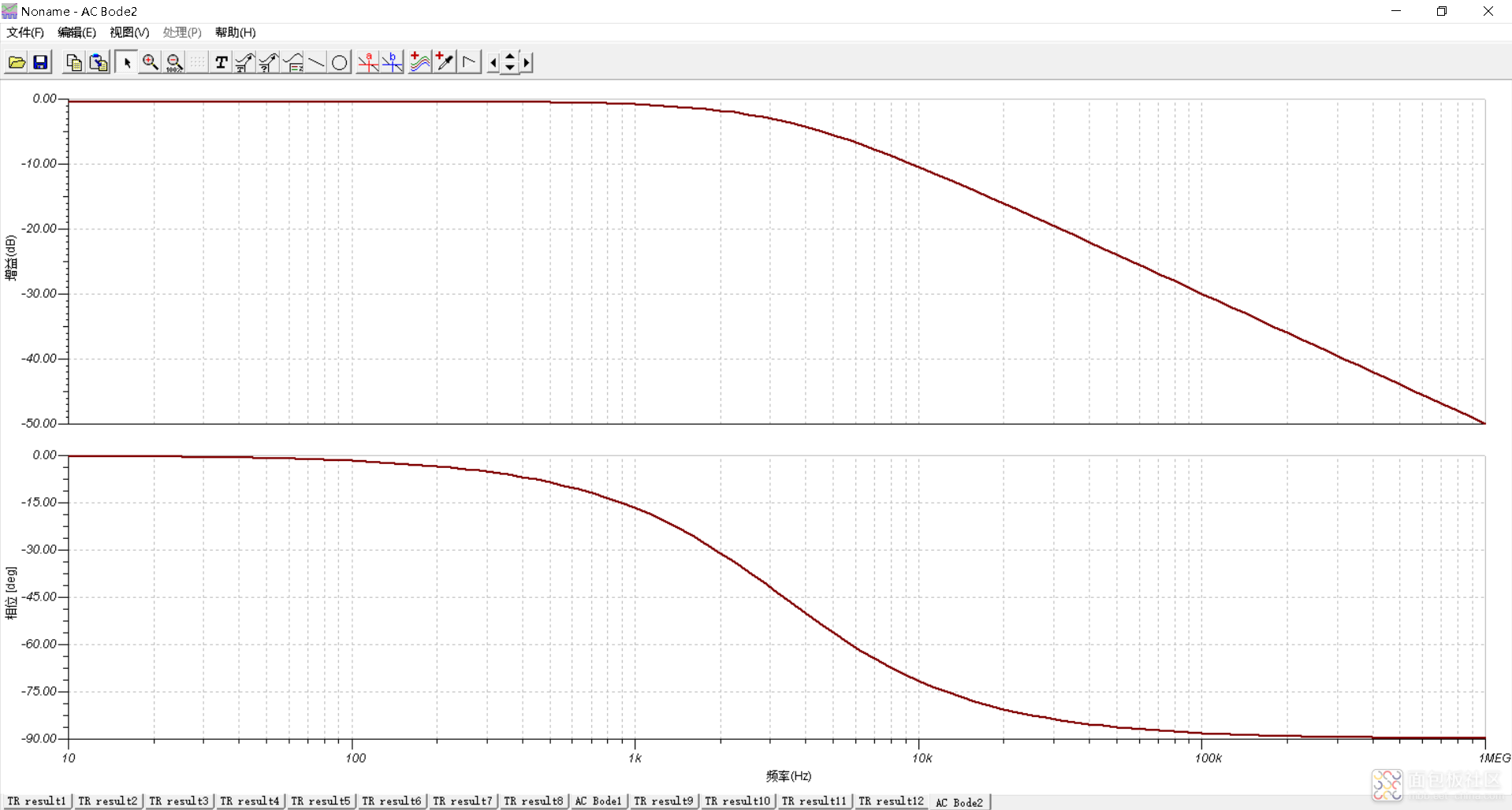
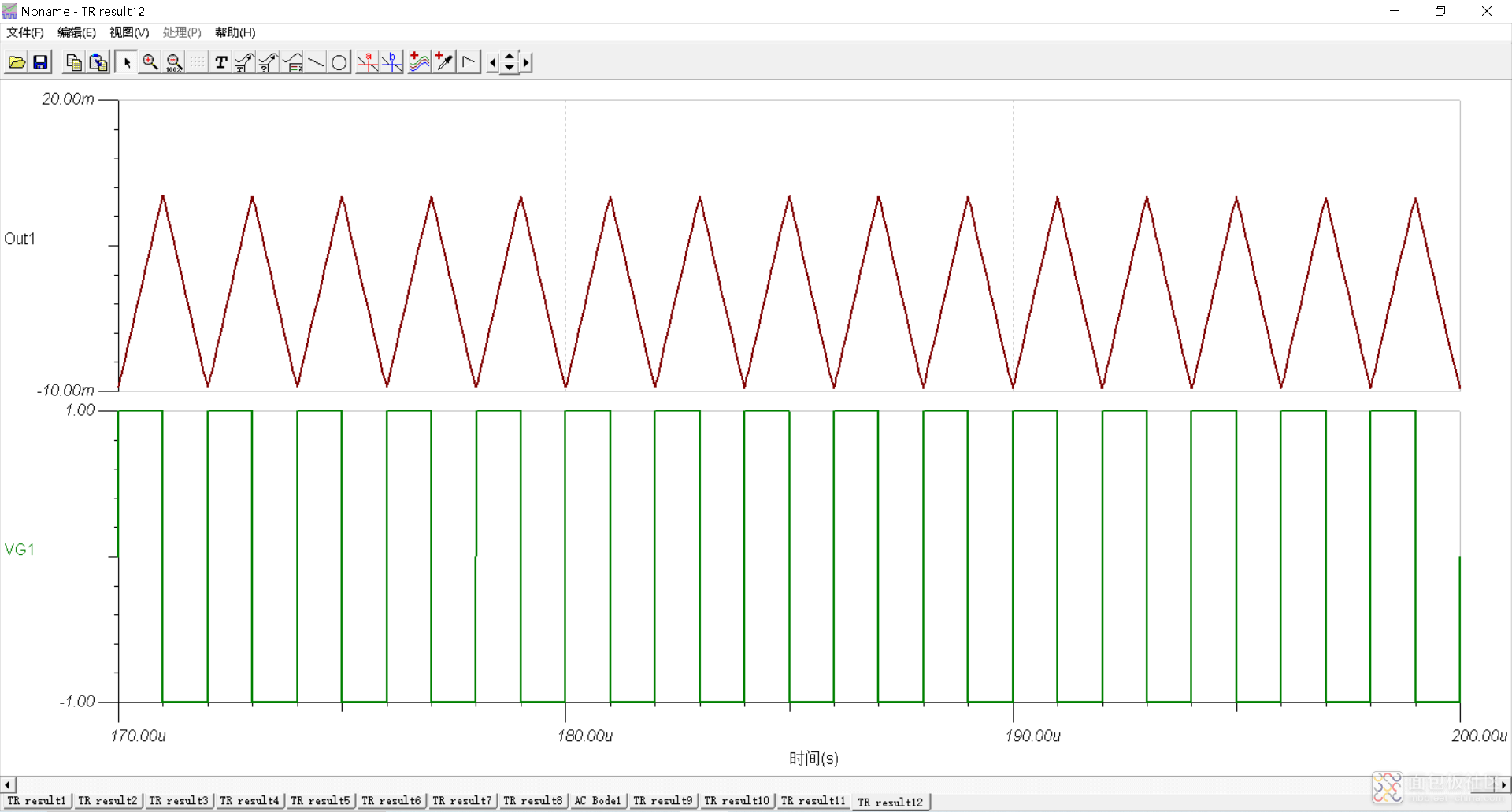
从后两张图片结果可以看出这种RC并联电路结构有滤波作用,但是又和一般的RC低通滤波电路原理不一样,由电容特性原理可知,电容两端电压不突变,信号加在阻容并联结构上边,对电容充电电容电压慢慢升高,电容钳制了电阻电压的上升。但是能不能像低通滤波器那样,给出一个传递方程呢?从量的角度分析这种电路结构滤波的原理?
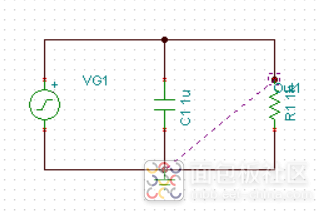

看到一个高速电路,两个运放之间有一个阻容并联结构,目的是为了滤波,搭建了一个简单的电路仿真一下,分别用方波作为输入信号源和交流参数扫描,所得结果如下:



从后两张图片结果可以看出这种RC并联电路结构有滤波作用,但是又和一般的RC低通滤波电路原理不一样,由电容特性原理可知,电容两端电压不突变,信号加在阻容并联结构上边,对电容充电电容电压慢慢升高,电容钳制了电阻电压的上升。但是能不能像低通滤波器那样,给出一个传递方程呢?从量的角度分析这种电路结构滤波的原理?



 /1
/1 

首先,我们需要明确几个基本概念:
1. RC低通滤波器:由一个电阻(R)和一个电容(C)串联组成,它允许低频信号通过,而抑制高频信号。
2. RC高通滤波器:由一个电阻(R)和一个电容(C)并联组成,它允许高频信号通过,而抑制低频信号。
在您提到的电路中,阻容并联结构可能起到以下作用:
电压钳制:电容可以在其两端电压达到某个阈值时限制电压的进一步上升,类似于二极管的钳位作用。
瞬态抑制:对于快速变化的信号,电容可以提供瞬态电流,从而抑制快速的电压尖峰。
要分析这种电路的滤波原理,我们可以尝试建立一个简化的模型。假设输入信号为\( V_{in}(t) \),电阻为\( R \),电容为\( C \),输出电压为\( V_{out}(t) \)。由于是并联结构,电路的总阻抗为\( Z_{total} = \frac{1}{\frac{1}{R} + \frac{1}{j\omega C}} \),其中\( j \)是虚数单位,\( \omega \)是角频率。
传递函数\( H(j\omega) \)可以表示为:
\[ H(j\omega) = \frac{V_{out}(j\omega)}{V_{in}(j\omega)} = \frac{Z_{total}}{R + Z_{total}} \]
在低频(\( \omega \rightarrow 0 \))时,电容\( C \)的阻抗非常大,\( Z_{total} \approx R \),传递函数接近1,这意味着信号几乎无衰减地通过电路。
在高频(\( \omega \rightarrow \infty \))时,电容\( C \)的阻抗非常小,\( Z_{total} \approx \frac{1}{j\omega C} \),传递函数接近0,这意味着信号被大幅度衰减。
因此,这种阻容并联结构在一定程度上可以看作是一种高通滤波器,但它与传统的RC高通滤波器不同,因为它的截止频率不是由单一的RC乘积决定,而是由电阻和电容共同决定的。
要更准确地分析这种电路的滤波特性,可能需要考虑电路的具体工作条件和信号特性,以及可能存在的其他元件和非理想因素。在实际应用中,电路设计者可能会根据需要调整电阻和电容的值,以达到预期的滤波效果。