第一讲 绪论与线性时不变系统
（Razavi教授打开平板电脑，站到讲台中央对着大家说:”Hello everyone, welcome to EE215A. How are you today? Good? Excellent! Let’s get started…”）
模拟系统是指系统中的信号量在一定范围内连续可变的系统（与之相反，数字系统中信号只能取离散的0或者1）。为什么我们要研究模拟系统？有两大原因。其一，自然世界中的信号本质是模拟的，比如声音和图像。人们需要在将这些模拟信号作一定处理（放大，滤波等等）后使用模数转换器转换为数字信号，才能为后续的数字系统所使用。其二，数字信号在非理想介质中传播时会发生衰减和失真，因此我们需要把这些数字信号当作模拟信号来处理才能在接收端顺利地恢复信号。例如在上图的例子中可以看到数字信号经过USB线缆的衰减到了接收端已经非常难看，需要使用模拟均衡器（equalizer）处理后才能恢复正确的波形。
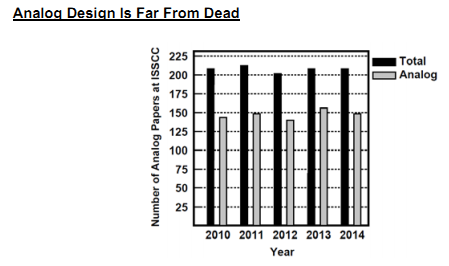
模拟电路是电子系统中必不可少的一部分，而且也是业界和学术界研究的热点。在2010年-2014年的国际固态半导体电路会议（ISSCC，全球最好的集成电路学术会议，每年都有大批来自工业界和学术界的顶尖成果在该会议中发表，被称为“集成电路界的奥林匹克盛会”）中，和模拟电路相关的论文占到60%以上（这个数字一直到今年的ISSCC都是如此）。从另一方面，这也说明模拟电路的设计存在各种挑战，需要我们不断创新来解决问题。
模拟电路会遇到多方面的挑战。首先，模拟电路需要更多的折中。设计者必须全盘考虑功耗，速度，增益，电源电压才能得到一个最优的设计。第二，模拟电路中的信号是连续的，因此相比数字信号噪声容限（noise margin）更小，更容易受到噪声和串扰的影响。第三，模拟信号对半导体器件的非理想因素（如非线性）很敏感。第四，模拟电路的综合很难使用自动化工具，而是需要设计者手工完成。第五，模拟电路相比数字电路更难建模和仿真。数字电路只需要使用布尔逻辑和延时两个参数即可完成建模，而模拟电路建模需要的参数（增益，带宽，瞬态响应，输入输出阻抗，非线性失真等等）远多于数字电路。因此数字电路仿真最常见的方法是使用带反标延迟的Verilog网表，而模拟电路仿真则需要SPICE网表，复杂度和文件大小远高于晶体管数目相同的数字电路。最后，模拟电路更容易受到工艺，电源电压和温度（PVT）的影响。总之，模拟电路的设计充满挑战，需要设计者认真对待。
（Abidi教授从文具盒中取出一支粉笔，清了清嗓子说:”Let’s begin from fundamentals…”）
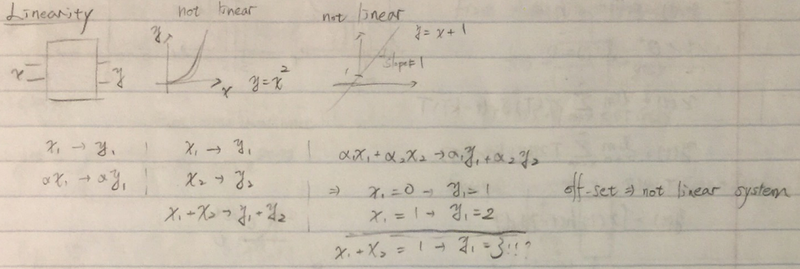图片.png1018x343 327 KB 大多数模拟电路可以用线性时不变（linear time-invariant, LTI）系统来近似。对于线性系统f(x)，需要满足：
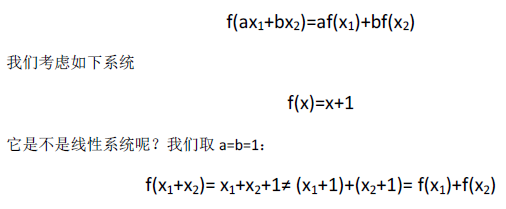
所以它不是线性系统。
对于时不变系统，当输入发生延迟Δt时，输出也相应延迟Δt。
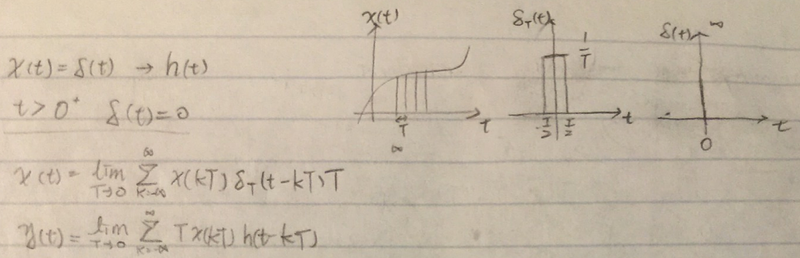
图片.png962x311 289 KB LTI系统可以由冲激响应（impulse response）来定义。当输入x(t)为冲激函数时，我们把系统的输出响应h(t)称为冲激响应。由于任意输入x(t)都可以近似表示为冲激函数序列的和，相应的系统响应可以表示为输入和系统冲激相应的卷积（具体请参考《信号与系统》课本）。
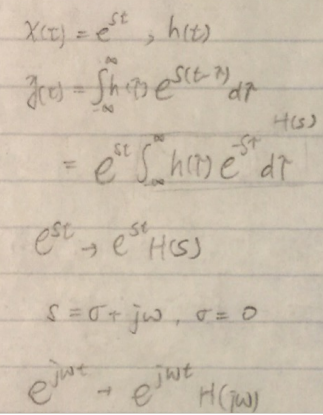
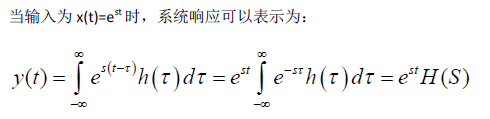
其中H(s)是h(t)的拉普拉斯变换，而s=σ+jω。H(s)也常常称为系统的传递函数(Transfer Function)。
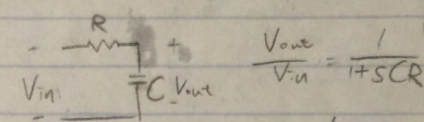
一个简单的传递函数的例子是RC串联电路。可以很容易地得到传递函数H(s)=1/(1+SCR)。
第二讲:传输函数，零极点的形成及时域响应
(Abidi教授，用粉笔敲了几下黑板，双手叉腰说道:”Let’s resume!”)
其中“*”表示卷积运算。同时，对于LTI系统，对于输入激励f(t)的响应y(t)正是f(t)与系统冲激响应h(t)的卷积。因此，系统响应y(t)的拉普拉斯变换Y(s)正是输入激励的拉普拉斯变换F(s)和系统冲激响应的拉普拉斯变换（即系统传输函数）H(s)的乘积：
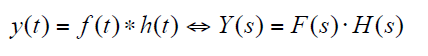
因此，我们可以很方便地在拉普拉斯域处理LTI系统，并且把得到的Y(s)做拉普拉斯反变换来得到系统的时域响应。更方便的是，当多个LTI系统级联在一起的时候，我们可以通过把多个系统的传输函数相乘来得到总的系统传输函数。
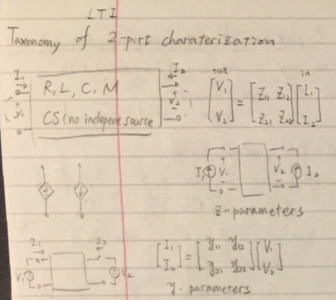
在线性电路分析中，最重要的一类LTI系统是二端口网络，因为大多数基本电路都可以用二端口网络来近似描述。二端口网络由传输函数矩阵来描述。举例来说，我们可以用Z参数（矩阵）来描述一个二端口网络：
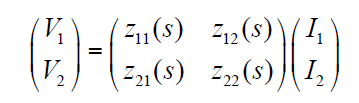
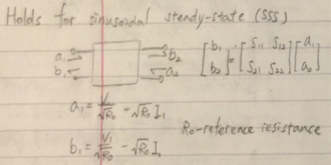
除了z参数之外，常用的二端口网络传输函数矩阵还包括y参数（z参数的对偶，输入为电压而输出为电流），混合参数（混合=hybrid=h，即h参数，输入包括电压和电流，输出也包括电压和电流），以及在射频微波电路中得到广泛应用的散射参数（散射=scatter=s，即s参数，输入和输出是在两个端口的入射/反射波幅度）。
（敲黑板：以上是对二端口网络的简单回顾，接下去要讲的二端口网络传输函数以及零极点的性质是这一讲的重点）
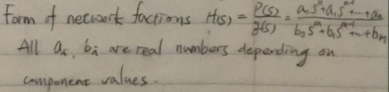
对于二端口网络传输函数矩阵中的任何一个传输函数H(s)，我们都可以写成如下形式:
对于实际二端口网络，分子p(s)和分母q(s)的根是实数或者是共轭复数对。所以我们可以把H(s)写成
从时间域上，极点和零点会影响二端口网络的瞬时响应（就是大家做仿真时候看的transient）。例如如果有些零极点对会造成电路输出上升下降时间很慢。二端口网络拉普拉斯域输出Vout(s)即输入Vin(s)与传输函数H(s)的乘积：
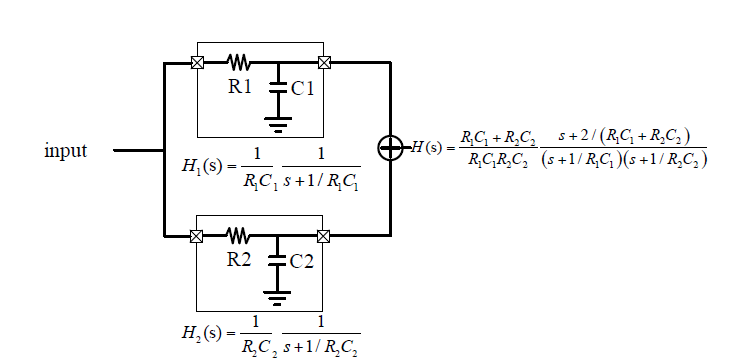
电路中的相移器件（电容C1和C2）产生极点（1/R1C1和1/R2C2），而信号经过两条极点位置不同的通路（H1和H2）相加产生了额外的零点（2/(R1C1+R2C2)）
二端口网络输出的时域响应可以通过对Vout(s)做拉普拉斯反变换得到：
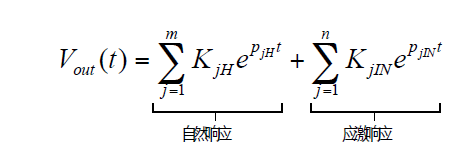
可以看到，一旦有任何一个极点的实部大于零（p=σ+jω，实部为σ）都会造成输出响应随时间指数增长，造成系统不稳定。实际电路中输出幅度不可能无限大，因为在输出幅度增长到一定程度后电路的非线性就开始占主导，于是在实际电路中不稳定现象表现为震荡。所以一个系统若要保证稳定，其传输函数的极点必须实部都小于0（当系统存在实部等于0的极点时该系统为临界稳定）。
以下为Abidi博士生同时也是215A助教哥的补充：
这里补充一个重要的概念：网络的极点PjH 只由网络的拓扑结构决定。只要激励不改变网络的拓扑结构， 任何传输函数的极点都不会改变。激励响应的位置决定了零点的位置。在零状态响应时，激励一定会触发网络的自然响应(即偏微分方程的通解)，同时也会建立受迫响应(即偏微分方程的特殊解)。网络每一个自然响应被触发了多少，由自然响应部分的拉普拉斯变换做部分分式展开后得知，而决定部分分式展开系数的是分子上零点的位置。
所以，找极点要看电路纯粹的拓扑结构，找零点要看激励和响应相对的位置。
有些时候，激励和响应的位置会很特殊，零点和极点完全一致从而互相抵消，这时候，就会有一个自然响应不会被触发。
下面来举一个Prof. Abidi 课上讲的例子：
Lattice network (or bridge network)
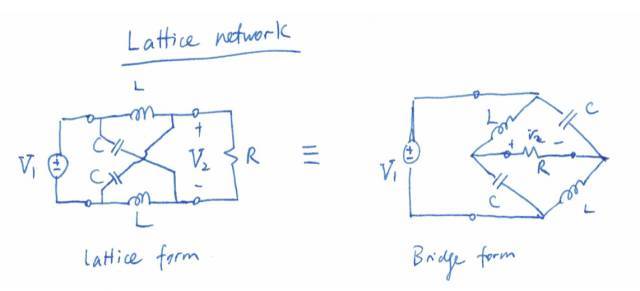
如果我们需要找传递函数 V2/V1 ，最直观的方法当然是硬解电路，算出V2与V1的关系。然而，Prof. Abidi 通过这个例子教会我们怎么用更深刻的方法寻找和理解极点和零点。
首先我们先假设V2=0找零点。如果V2=0， 那么通过R的电流为0，所以可以直接计算在R两端的电压（通过分压）。
我们发现这个传输函数有4个零点。
下面我们找极点，极点是由电路纯粹的拓扑结构决定的。所以我们要把独立源V1去掉，然后找电路的自然响应。很多情况下，自然响应可以通过电路的对称性或者重新把电路画成几种基本型来找到。Prof. Abidi正是用了这种方法。
所以，这个电路有四个极点，(本科电路基础：极点的个数由独立状态变量的数目决定）。但是，其中两个极点会与两个零点抵消，所以最终的V2/V1 的零极点图如下图
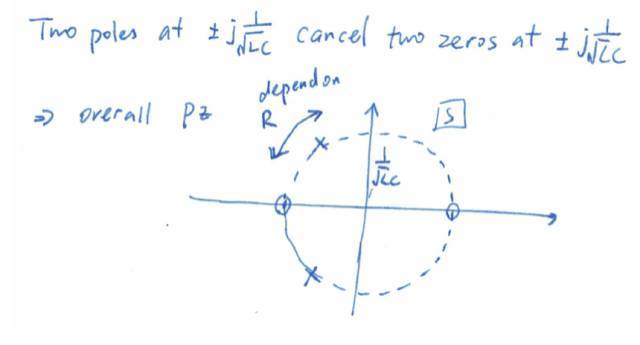
第三讲:零极点与频率响应
上一讲我们讨论了零极点的形成及其时间域响应。这一讲我们从频率域来分析零极点的影响。从频率域上，零点和极点会决定系统的频率响应。我们令系统传输函数H(s)中s(=σ+jω) 的实部σ=0而虚部ω仍然是变量，就得到了频率响应函数H(jω)。频率响应函数代表系统在恒包络正弦小信号输入时，输出正弦信号相对输入正弦信号的幅度和相位变化。频率响应函数可以表示为：
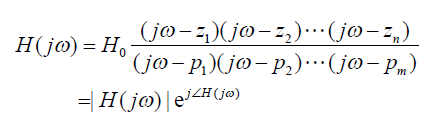
频率响应H(jω)是复数。其幅度|H(jω)|代表当正弦信号频率为ω时，输出正弦信号幅度相对输入正弦信号幅度的比值（即系统的增益），而其相位∠H(jω)则代表输出正弦信号相对输入正弦信号的相位变化。根据高中数学，频率响应的幅度和相位可以表示为各个零点/极点的贡献：
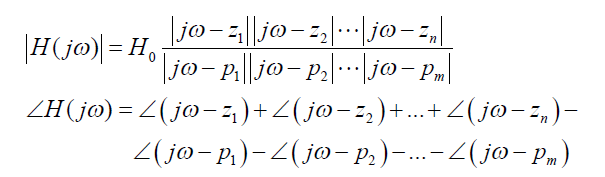
我们来看一个简单的例子。一个系统的频率响应为:
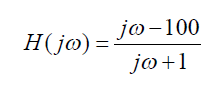
它有一个极点（实部σ=-1,虚部ω=0，其模为1）和一个零点（实部σ=10,虚部ω=0，其模为100）。由于极点的实部小于0，该系统是稳定的。当ω=0的时候[即DC（直流）响应]，分母的模为1，相位为0，分子的模为100，相位为π，因此频率响应的幅度为100，相位为π。我们接下来增加一点点ω，让它等于0.001。这个时候ω远远小于极点的模，因此频率响应分母的值和DC时没有显著区别(1+j0.001≈1)。ω也远远小于零点的模，因此频率响应分子的值也和DC时基本相同。所以当ω的值远远小于某个极点/零点的模的时候，该极点/零点的效应可以忽略不计。这也是在实际电路设计中很多频率远高于电路工作频率的极点/零点在分析的时候可以忽略的原因。当ω增加至1时，分母变为(j1+1)，此时分母的幅度由DC时的1变为√2，相位则由0变为π/4。由于ω仍然远小于零点(1<>100)时，频率响应的分子可以近似为jω，因此分子的相位为π/2，且分子的模随着频率增长以20dB/dec的速度增长。此时分子和分母的模都以20dB/dec增长，因此互相抵消，频率响应的幅度不再变化，而相位则由DC时的π变为0。
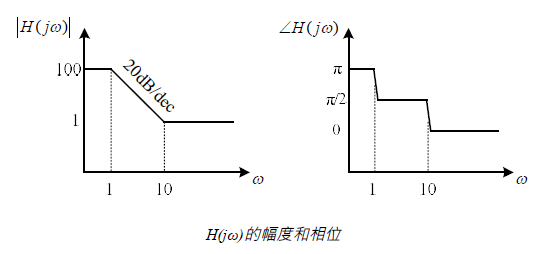
零点和极点对频率响应的效果也可以由s平面零极点图解释。上面例子的零极点图如下：
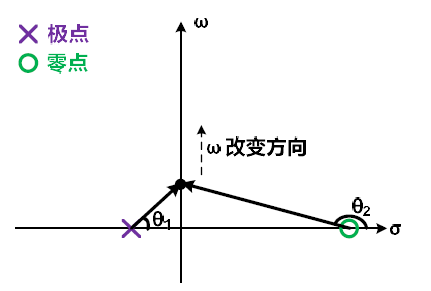
图中的平面是s-平面（s=σ+jω），横轴是σ而纵轴是ω。对于频率响应，我们固定σ=0而改变ω,相当于图中黑色的点沿着纵轴方向改变。连接零点/极点和ω的向量表示零点/极点对频率响应的贡献。频率响应的幅度等于所有连接ω和零点的向量长度之积比上所有连接ω和极点的向量长度之积，而频率响应的相位等于所有连接ω和零点的向量与σ轴的夹角的和减去所有连接ω和极点的向量与σ轴的夹角的和。举例而言，我们来看看极点向量随频率的变化。
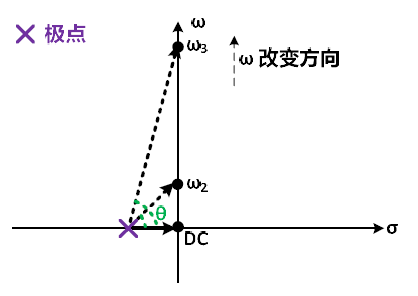
已开始ω1=0(即DC响应)，极点向量的相位为0。之后随着ω增加，极点向量的长度逐渐增长，相位贡献θ也逐渐变大。当ω等于极点的模的时候(ω2)，根据初中数学极点向量的长度变为DC时的√2倍，而相位角θ为π/4。之后随着ω继续增长到远大于极点的模的时候，极点向量渐渐变得和ω轴平行，此时极点向量的长度近似等于ω，而相位角θ也渐渐逼近π/2。对于零点也可以做类似的分析。这样图解分析与之前分析的结果相同，但是更直观。
零点和极点对频率响应的影响可以总结为：
*当频率远小于某零点/极点的模时，该零点/极点对频率响应的影响可以忽略。
*当频率接近某极点的模时，该极点的效果渐渐体现。当频率远大于该极点时，该极点使得频率响应的幅度以20dB/dec的速度衰减，而相位相对DC产生-π/2的变化。
*共轭极点是一种特殊的极点，它们总是成对出现且共轭极点对的模都相等，因此当频率远大于一对共轭极点的模的时候，该共轭极点对会使频率响应的幅度以40dB/dec的速度衰减，而相位相对DC产生-π的变化。而在频率接近共轭极点对的模的时候，频率响应曲线的变化取决于共轭极点对的位置（详见下文）。
*当频率接近某零点的模时，该零点的效果渐渐体现。当频率远大于该零点时，该零点使得频率响应的幅度以20dB/dec的速度增加。而相位相对DC产生π/2（当零点在左半平面）或-π/2（当零点在右半平面）的变化。
*频率响应的总体幅度/相位取决于所有零点和极点对幅度/相位的贡献。
共轭极点对
共轭极点对模型最初来源于LC谐振电路，如下图中的RLC串联电路。
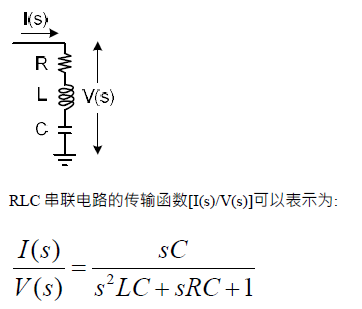
其中共轭极点的谐振频率ω0=1/√LC即LC tank的谐振频率，品质因数Q=(1/R)∙√(L/C)即为LC tank的品质因数，表示在谐振频率附近每周期LC tank存储的能量与耗散能量的比值。共轭极点可以由LC tank形成，也可由反馈通路形成。
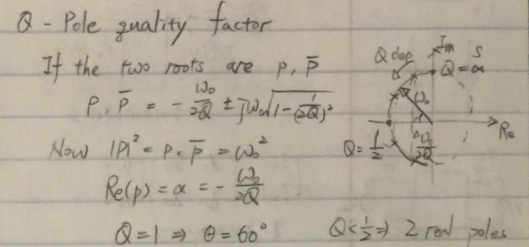
共轭极点对的Q值由共轭极点的位置决定。当共轭极点的谐振频率固定而改变品质因数（即固定L和C而改变R）时，共轭极点对的轨迹在以原点为圆心，半径为ω0的圆上。当共轭极点对靠近纵轴时，品质因数变大；而当共轭极点对靠近横轴时，品质因数变小。共轭极点对的品质因数必须大于等于1/2，当Q小于1/2时共轭极点对退化为两个实极点。
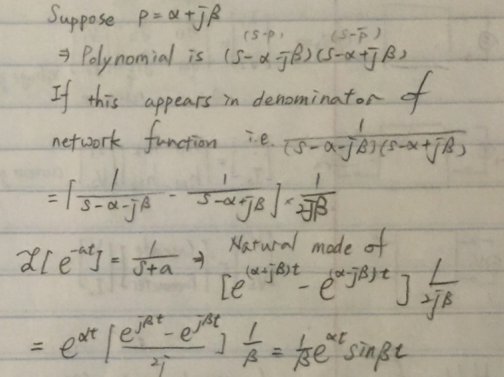
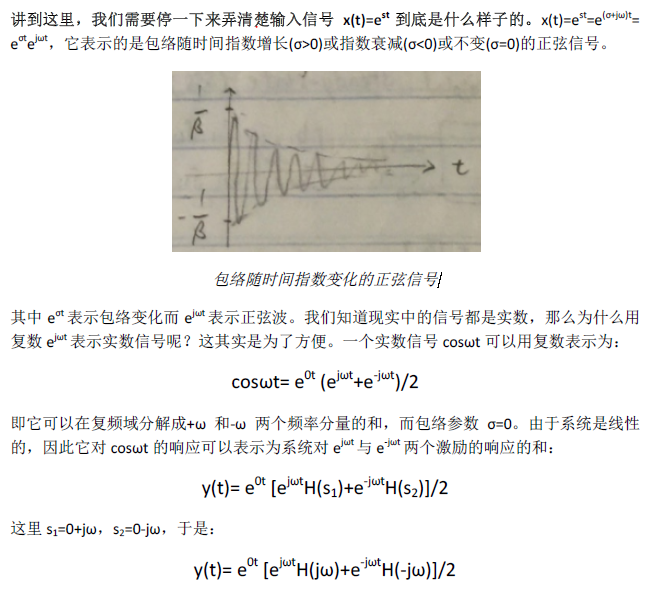
对于传输函数具有共轭极点对的系统，系统的自然响应中含有包络指数衰减的正弦波。有时候在放大器的瞬时响应中会看到衰减震荡的现象，这种现象就是由共轭极点造成的。
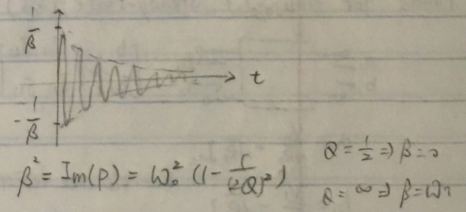
正弦波的频率接近谐振频率ω0，而包络的衰减速度取决于Q。Q值约等于包络衰减到初始值的1/e时所需要的谐振周期。Q值大时包络衰减较慢，反之Q值小时包络衰减较快。在放大器设计中我们往往希望看到settling time比较小的瞬时响应，因此应该避免高Q值得共轭极点对。
共轭极点对另一个重要性质是它会引起频率响应的尖峰(peaking)。这一点可以从零极点图来理解。
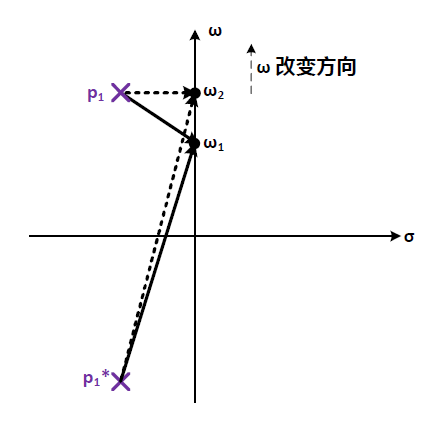
在零极点图上，有共轭极点p1和p1*，位置在σ±jω0。当频率从ω1(略小于ω0)移动到ω2(等于ω0)时，连接到极点p1*的极点向量长度基本不变，但连接到极点p1的极点长度显著变短了。因此频率响应在谐振频率(ω=ω0)处会产生一个尖峰，尖峰的高度随Q值变大而变大。极端情况是Q值无穷大时，此时p1和p1*都在ω轴上，因此当ω=ω0时，连接p1和ω的极点向量长度为0，这样频率响应的幅度变为无穷大，所以就产生了高度无穷大的尖峰。在设计需要较小settling time的放大器时我们希望避免明显的频率响应尖峰（频率响应尖峰明显=>共轭极点对Q值大=>瞬时响应中衰减震荡持续时间较长=>settling time较长）；但另一方面在设计宽带放大器（例如在CML电路中）时我们往往会故意引入频率响应尖峰以增加带宽。
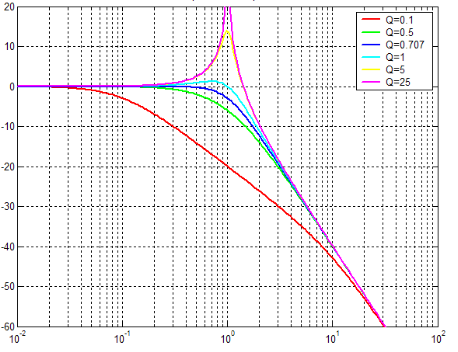
频率响应尖峰与Q值的关系
至此我们回顾了EE215A所需要的电路分析基础知识。接下来我们将应用它们去分析具体电路。
EE215A 的助教哥又回来啦！这次给大家带来传输函数标准型的补充
将传输函数写成标准形式有助于我们迅速画出频率响应的草图，这对我们今后分析放大器、锁相环的噪音和稳定性至关重要。
一阶零极点
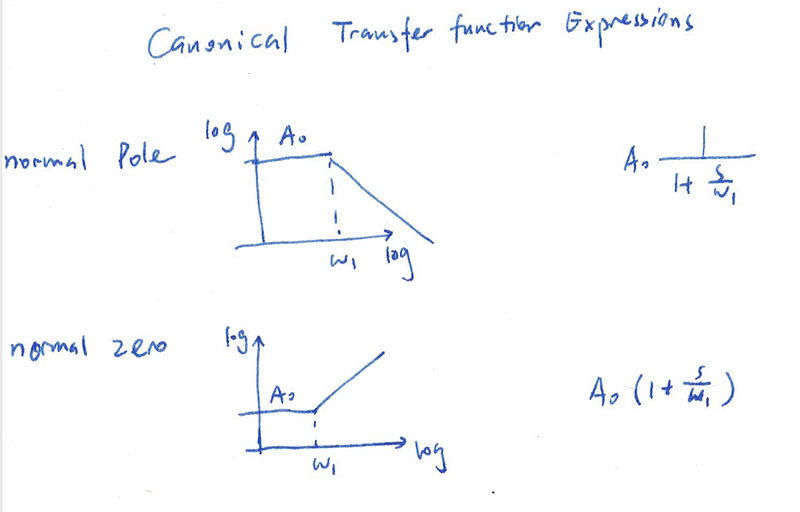
之前说的零极点是标准的零极点定义，也可以称为正向零极点。注意我们要把极点，零点写成归一化的形式，便于我们将基准增益拆分出来。在下图中，基准增益都是A0
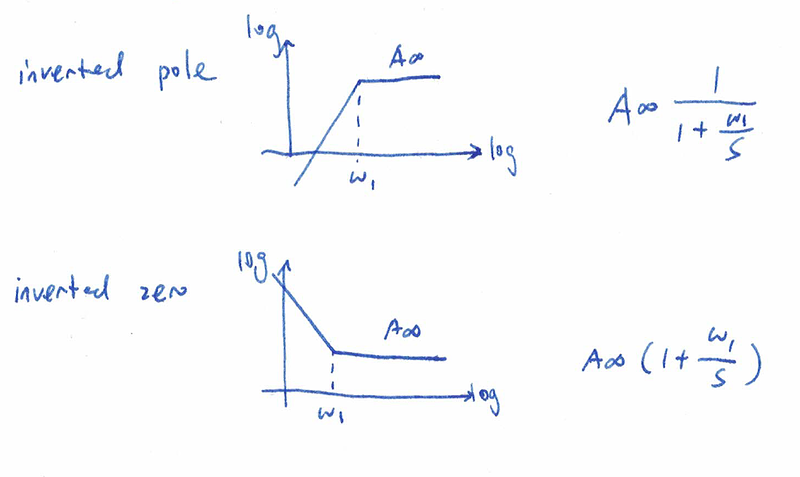
图片.png995x637 140 KB 逆向极点和逆向零点是新引入的概念。逆向极点的意思是如果从无穷高频率出发向DC 移动，频率响应会遇到一个-1斜率滚降(或者叫-20dB/dec如果用分贝)。同理，逆向零点是从无穷高频率出发向DC 移动，频率响应会遇到一个+1斜率上升(或者叫-20dB/dec如果用分贝)。逆向极点是由一个在原点的零点和一个在ω1的极点组成。逆向零点由一个在原点的极点和一个在ω1的零点组成。如果我们将传输函数写成如下的逆向形式而不是一般的正向形式，频率响应就能很快被画出来。
图片.png966x577 117 KB 正向、逆向极点和零点的相位响应曲线大家可以很容易想出来，只要注意频率变化方向即可，所以就不重复讲了。
灵活运正向、逆向零极点对于分析这对我们今后分析放大器、PLL的噪音和稳定性至关重要。下面举个例子：
图片.png1083x806 188 KB 二阶零极点
我们先重新学习二次函数的根的表达式。我们在高中学的二次函数根长这样：
图片.png1102x287 92.2 KB 但是问题是，这样的表达式是高熵的，比如某一个传输函数的分母的根按照传统高中学过的表达式，长这样：
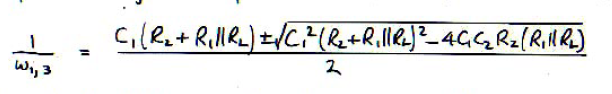
你看这个表达式，长得这么丑，看着就浑身难受。除非你用一个绘图软件，并把所有R C的值带入，否则你没有办法快速找出这两个根的关系，没法根据这个表达式快速绘出频率响应。更重要的是，你没有办法从这个表达式快速看出要怎样设计R C以达到你的目的。
所以Prof. Abidi（原引Prof.Middlebrook）教育我们要用适合电路设计的二次函数根式。
回去看高中根式，其实这个根式用的是两根之和等于-b/a 的性质。但是二次函数两根之积还等于c/a，新根式正是运用了两根之积性质。换句话说，高中公式看的是两根的算术平均，新根式看的是两个的几何平均。不要忘了在对数刻度中，几何平均比算术平均更加有意义，因为两个刻度的中点是几何平均。
新根式如下：
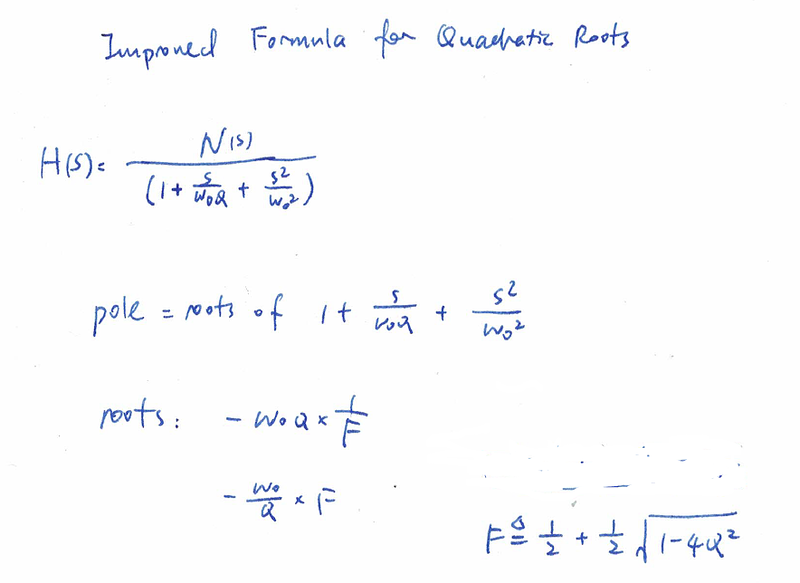图片.png884x645 120 KB 注意看新根式的对称性！拿到一个二阶表达式，我们只要算Q和ω0就可以了。有同学会问，那F怎么办，F不是还是乱糟糟么？其实不然，我们把F和Q的关系画一下：
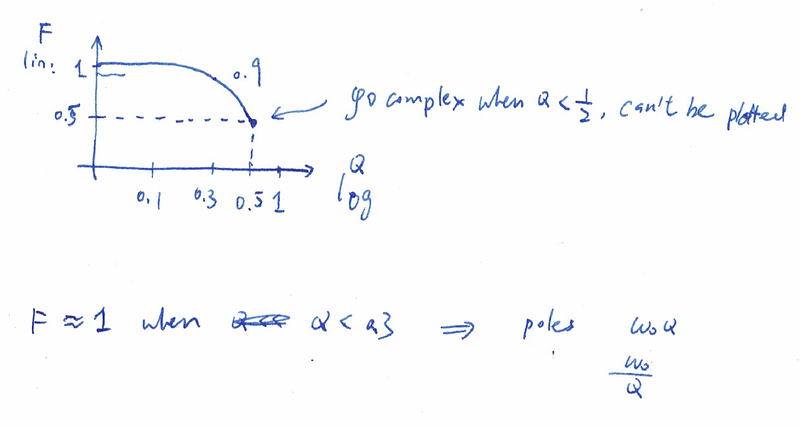图片.png980x524 110 KB 你看，当Q小于0.3的时候，F约等于1。所以我们只要根据Q的表达式，估计Q值，如果远小于0.3，那么就是两个实根，一个是-ω0Q，另一个-ω0/Q 啦！
有同学会问，那Q 在0.3和0.5中间时候怎么办呢？很简单，把他们近似成两个重实根就好了。
如果Q大于0.5，我们就有复数根（共振）了。
这样的表达式利于具体的电路设计。我们可以分析电路模型，把ω0和Q用电路元件的参数表达出来。之后比如我们可以设计 ω0 以达到带宽要求。设计Q 以达到稳定性要求。
二阶带通
二阶带通标准形式如下，零级点图中画的是极点的轨迹（随Q变化而移动）。
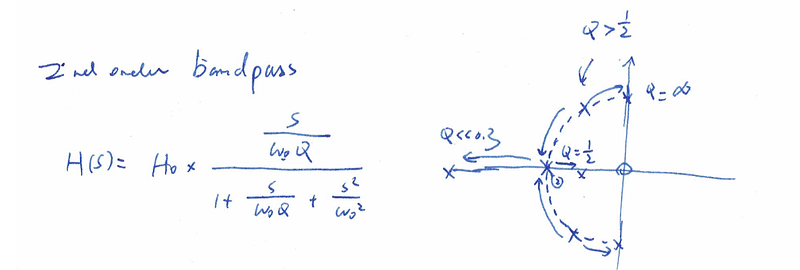图片.png1317x446 146 KB 
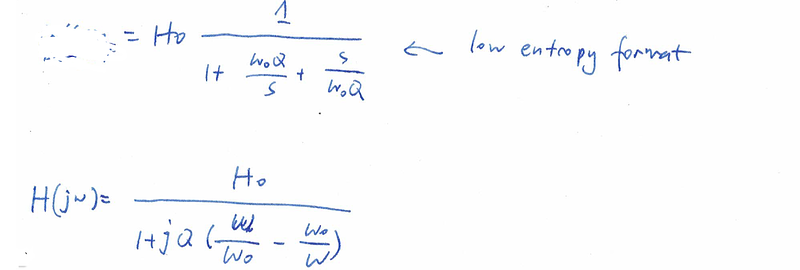图片.png1317x445 113 KB 通过新根式，我们可以画出幅度频率响应
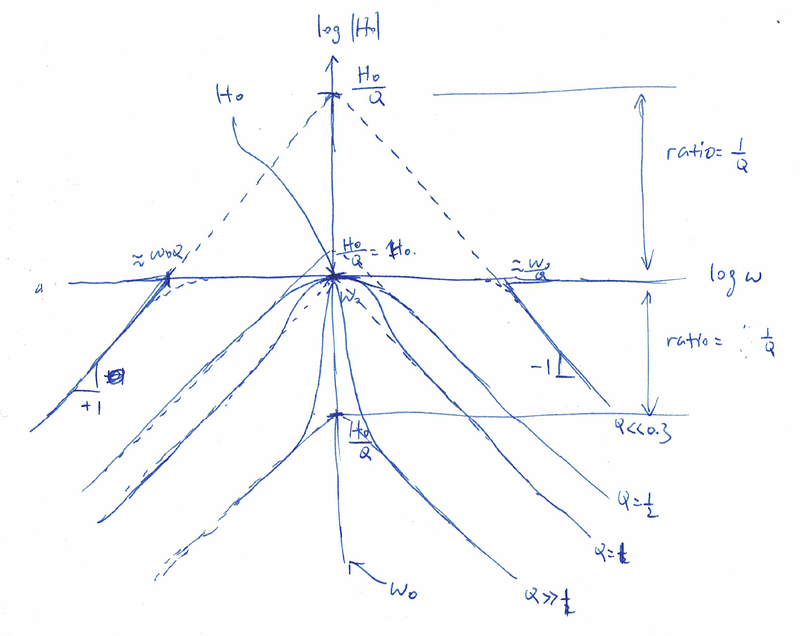
图片.png1069x850 250 KB 纵轴时|H| 对数刻度，横轴是ω对数刻度。
中间交汇处是H0，ω0。不管Q为何值，幅度响应都在ω0通过H0。
当Q小于0.3时，双实根距离很远，我们有一个正向极点和一个逆向极点。
当Q等于1时，两个渐近线的延长线正好交汇于H0，实际响应有一个小尖峰。
当Q远大于1时，两个渐近线交汇于H0/Q 很低的一个点，但是|H|还是要过H0，所以有一个很大尖峰。
相位响应（近似渐近线）如下：
随着Q增大，角度变化越快。
二阶低通与二阶带通类似，只是少了一个零点
标准表达式如下
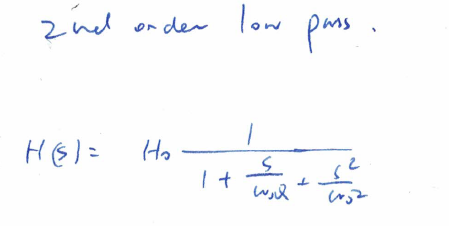
幅度响应如下
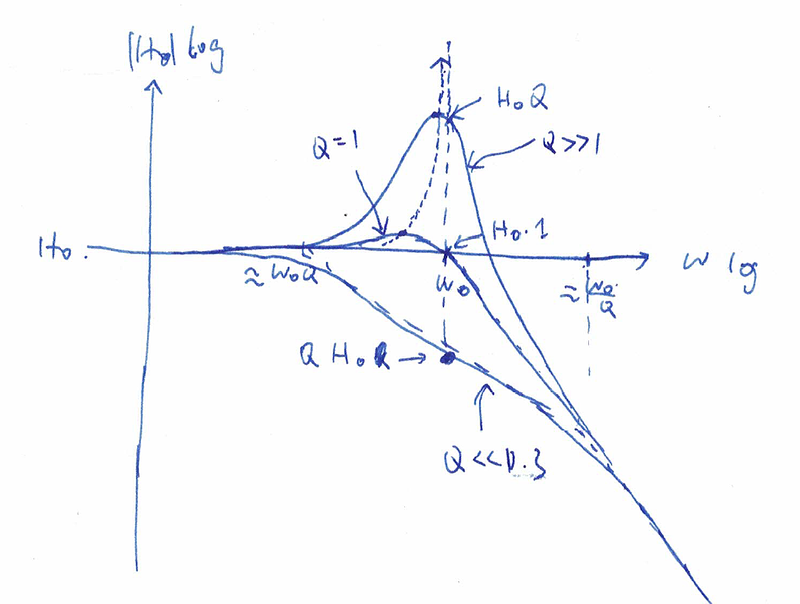
图片.png986x745 201 KB 记住幅度响应在ω0时为H0Q，所以当Q=1时幅度在ω0时为H0。但这时我们已经有微小的尖峰了。
注意幅度的最高点永远小于ω0，当Q增大时，无限接近于ω0。
二阶低通相位响应与带通的类似，只是整体向下移动90°。
同样地，我们可以定义正向二阶极点零点和反向二阶零极点，大家到此应该可以想出以下推论了。
（摘自Middlebrook）
来源：微信号 矽说
/3 
Excellent!