
最近在做一个温控电路时发现一个问题,既不知道补偿电路的经验值也不知道功率级的传递函数,PID的调试精髓尚未掌握,在初期调试中一片茫然。温控元件是一个半导体制冷器(TEC)温度控制在10度至60度,最大电流限制在2.5A。补偿电路采用的是Ⅰ型补偿。
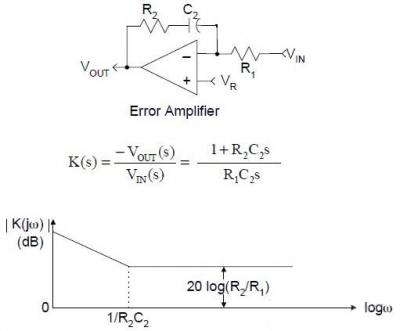
图1-1 Ⅰ型补偿电路
采用经验法要得到最优参数并不太容易,对于没经验的人来说就更不容易了。环路分析仪并不是每人都有,在思考如何得到功率级传递函数时想到一种反推法。
反推法是采用不合理的补偿环路参数让电路震荡并记录震荡频率,此时可认为补偿后的开环增益为0dB相移-180°,因为开关增益=补偿环路+功率级函数,而补偿环路参数是已知的所以可以反推出功率级传递函数。修改补偿环路参数可以得到不同的功率传递函数的点从而描绘出功率级传递函数曲线。
按照这种反推法得到的功率级bode图近似如下:
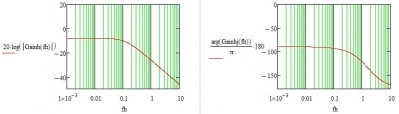
图1-2 加热电路功率级bode图
这里增益函数和相位函数可以独立(不同),如果要描述一个电路真实的传递函数还是很有难度的,将增益函数和相位函数分开只要曲线近似就可这样就大大降低了难度。
有了功率级传递函数后面的补偿就容易实现了,见下图:
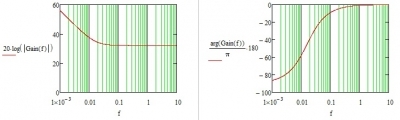
图1-3 补偿电路bode图
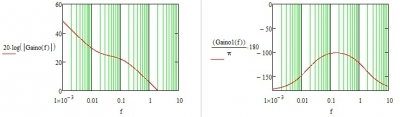
图1-4 总开环bode图
如图1-4 穿越频率约2Hz,相位余量约38°。
TEC温度响应实测如下:
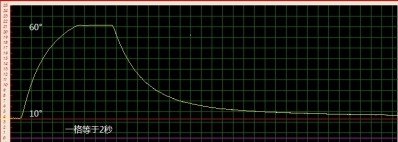
图1-5 实测TEC温度响应
图1-5是同事做的一个带波形显示的串口调试软件,可以将串口得到的数据转换成直观的波形。X轴每格代表2秒温度从10°升到60°大概需要5格既10s,温度从60°降到10°速度略慢,温度上升和下降速度主要受TEC的功率限制。从图1-5还可以观察到温度突变后并无明显的过冲现象,这说明由反推法得到的功率级传递函数还是可行的,如果有机会可以用环路分析仪或者软件仿真来验证这种反推法的准确性。
仿真Buck电路验证反推法
准备仿真一个Buck电路来验证这种反推法,电路如下:
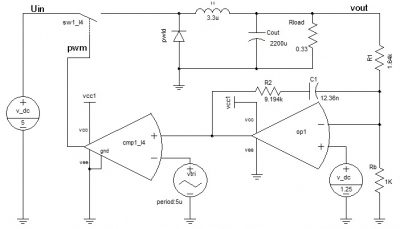
图2-1 Buck电路
电路的参考资料:
开关电源控制环路设计(初级篇).pdf (1.1 MB)
仿真文件:
bucktest.rar (3.6 KB)
通过仿真和Mathcad计算的结合验证了几个现象。
首先把图2-1中的R2改为0.9149k欧姆,输出结果如下:
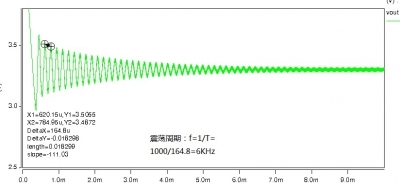
图2-2 输出欠阻尼震荡(条件稳定)
再观察此参数下的Bode图(总开环图)
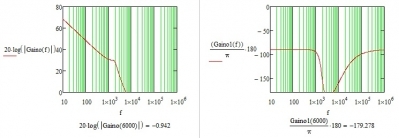
图2-3 条件稳定bode图
图2-3中右边的相位图有两个过零点一个在2.4KHz处一个在6KHz处,左边增益图穿越频率为6KHz。根据资料所说在穿越频率前如果相位超过-180度则会出现条件稳定,图2-2的这种欠阻尼震荡大概是条件稳定的一种表现形式。
把电阻R2改为276欧姆,电容C1改为40.36nF,输出结果如下:
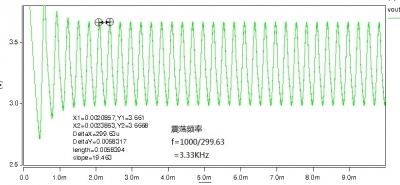
图2-4 等幅震荡
Bode图如下:
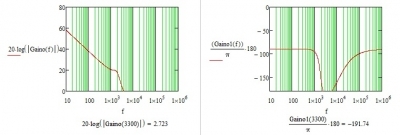
图2-5 等幅震荡bode图
图2-5中穿越频率处(约3.3KHz)相位超过了-180度,电路变成震荡电路。
将增益曲线继续左移,电容C1=480.36nF,电阻R2=23欧姆,输出结果如下:
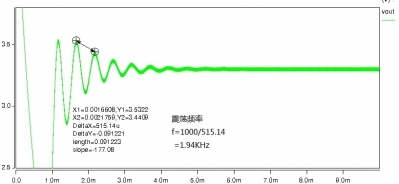
图2-6 开机震荡波形
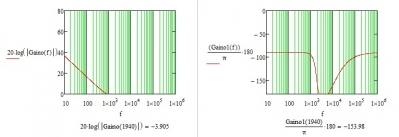
图2-7 开机震荡Bode图
图2-7中可能因为相位余量太小造成开机震荡。
环路参数配置合理的波形如下:
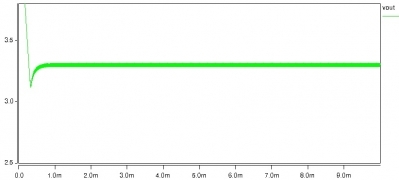
图2-9 合理参数下的输出波形
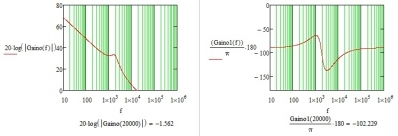
图2-10 合理参数的Bode图
电阻R2=9.194k欧姆,电容C1=1.236nF会得到条件稳定的通常情况:
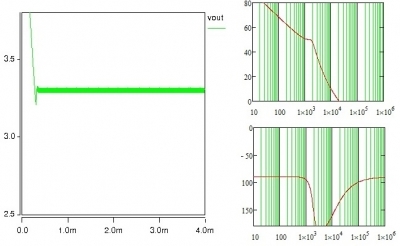
图2-3-1 条件稳定通常情况
看图2-3-1的输出电压是很稳定的,那么什么条件下会发生条件震荡?通常一个电路设计好后参数不会有太大漂移只剩下输出功率和输入电压这两个因素,通过Mathcad验证当输入电压变低时增益曲线会向着震荡的方向移动(图2-3-1增益曲线向左移动)。从这个结果看如果在设计环路时采用最低输入电压那么即使环路存在条件稳定也没有问题,因为电压已经是最低了会造成震荡的条件已被排除了。
反推法是调节环路中的参数使电路处于临界震荡状态,在这种状态下反推出的数据会非常接近功率级的Bode图,见下面一组数据。

表1-1 临界震荡参数表
将表1-1中后面的功率级增益和功率级相角绘制成曲线并同原电路的功率级Bode图对比如下:
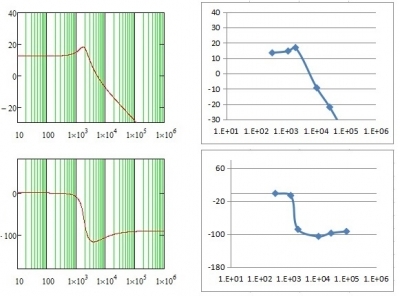
图3-1 原Buck拓扑bode图同反推bode图对比
如果忽略测试误差再多测几个点的话这种反推法基本可以描绘出一个未知电路的传递函数曲线,不过让电路工作于临界震荡状态并不容易尤其是在低频段如图3-1低频段的相位余量接近180度想震荡很难。表1-1的部分数据是在环路中增加了一级RC电路后才实现了低频震荡,高频震荡是工作于条件稳定状态既第二个过零点震荡。后续期望能找出一种更简单有效实现临界震荡的方法。
通过几组数据来验证相位余量对环路的影响,数据表如下:
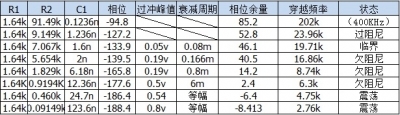
表1-2 不同相位余量数据表
这个表自上而下相位余量递减对应的状态由过阻尼逐渐过渡到震荡模式,见下面仿真图:
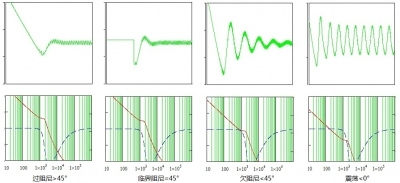
图4-1 相位余量逐渐变小的电路状态
工程上取相位余量45度恰好是临界阻尼状态,实际设计电路时多从可靠性考虑取略大于45度相位余量。(saber仿真和Mathcad略有差别,过阻尼>45°的图更接近临界阻尼,参考变化趋势即可)
上面图4-1存在条件稳定,通常没有条件稳定的情况如下:
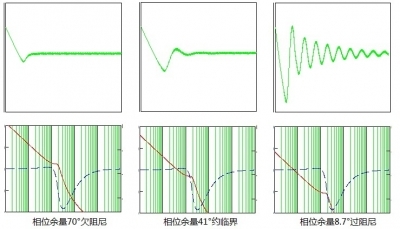
图4-2 欠、临、过三状态波形
在通常模式下规律也是相似的,相位余量45度为临界过度点。
来源:21世纪电源网




 /5
/5 


