但请记住,转换器是信号链的瓶颈,最终决定着信号的表示精度。因此,转换器的选择是设定系统整体要求的关键。
在信号链中,可能会累积的误差有两类——即直流和交流误差。
✍ 直流或静态误差(如增益和失调误差)有助于了解信号链的精度或灵敏度;
✍ 交流类误差也称为噪声和失真,限制着系统的性 能和动态范围。
这两类误差都需要了解,因为二者最终决定着系统的分辨率。本文将专门分析直流误差,根据其与无源和有源器件的关系, 对每种不精确性进行细分。
分析误差前,先对信号链分个级
图 1 是一种可以达到 0.1% 精度要求的简单数据采集系统,也就是说,每输入 1V 的电压,输出要么为 0.99388V,要么为 1.00612V。因此,转换器规定的动态范围为 60dB 或 9.67ENOB,假设其满量程电压为 10 V。转换器有两个放大器级、一个多路复用器和一个 ADC。本分析将忽略传感器、电缆、连接器、PCB 寄生电容和任何外部影响/误差,因为这些情况在很大程度上取决于我们要测量的具体应用或信号。
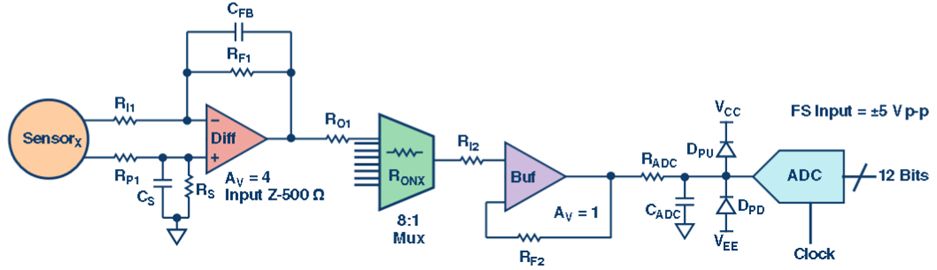
图1. 此简单数据采集信号链系统的设计精度为0.1%。
???? 第一级,一个简单的差分放大器 (图2)。该放大器的增益为 4×,输入阻抗为 500 Ω。设置电容是为了进行可选的滤波处理。

图2. 差分放大器为数据采集信号链的第一级。
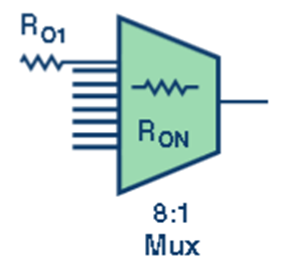
图3. 此 8:1 多路复用器有 8 个缓冲输入。
????第三级,将结果形成的通道信号施加到单位增益缓冲级放大器 (图4)。使用电阻是为了减少输入偏置电流不平衡。
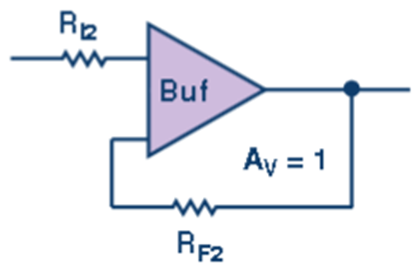
图 4. 将一个通道信号施加到这类缓冲放大器。
图5. 信号缓冲后将被施加到 12位、1 MSPS ADC。
接下来,我们将基于这里讨论的各个信号链级,考察无源误差和有源误差。
直流无源误差
所有无源组件都有误差与其相关,尤其是电阻。表面上看,电阻似乎是比较简单的器件,但实际上,如果其规格不符合设计要求,则在整个信号链中都有可能导致误差。这里不会讨论如何选择正确的电阻类型及其构成。但要记住,根据具体的应用,有些电阻类型可能比其他更合适。
阻性直流误差源于不理想的电阻容差。简单地指定容差值是不够的。然而,对电阻误差容差过分挑剔也可能产生不利影响,使得分析过于复杂。在为给定的信号链指定电阻类型时,至少要注意四个至关重要的技术规格:
- 值容差,单位通常为%。
- 温度系数或漂移,单位通常为ppm/°C。
- 寿命漂移或合格性,通常以指定小时数内的%为单位(通常为1000)。
- 值容差比,当网络中或同一封装中有两个或以上的电阻且值匹配时,值容差以%为单位。
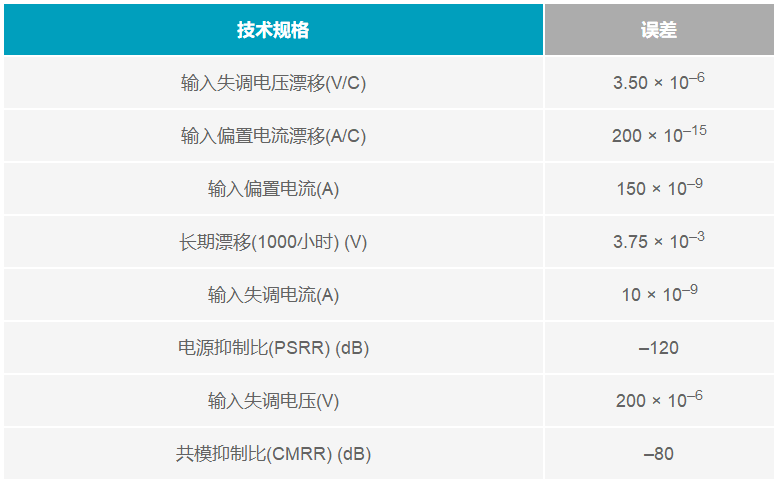
为了说明电阻误差是如何累积起来的 (图6),我们来看看下面这个例子:假设有一个 100 Ω 的电阻,其值容差为 1%,温度漂移为 100 ppm/°C,寿命容差为 5%,则在 5000 小时的寿命周期内,在 85°C 的温度范围内,其电阻为 93.15 Ω 至 106.85 Ω:
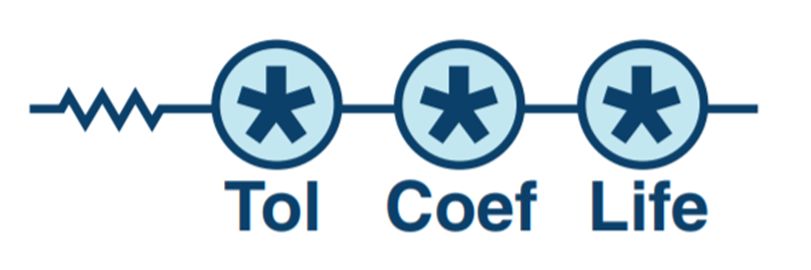
图6. 此图所示为一个电阻误差模型。
总容差(RVALUE + RTOL + RCOEFF + RLIFE) = (RVALUE + ((RTOL/100) × RVALUE)+ (((RCOEFF × 0.000001) ×温度范围) ×RVALUE) + ((RLIFE/100) × RVALUE))= 94 Ω 至106 Ω.
来之不易的信息边注
有些组件的寿命周期只有1000小时,但设计的要求可能要长得多,比如,10,000小时。为了解决这个问题,不要将1000小时乘以8.77 (8766小时/年);这样做太过悲 观了。任何精密模拟电路中的长期漂移都会有一定的“随机游动”量。正确的做法是用此数值的平方根,即 √8.766= ~3再乘以1000小时。因此,10,000小时的寿命周期为: √10.000= 3.16 × 1000小时,如此等等。
需要注意的是,电容和电感也有误差。但这些误差通常可以忽略不计,在这类直流分析里并无多大的价值。另外,这些器件实际上是无功器件,对滤波和带宽容差的影响最大,本文的直流分析里同样没有考虑这一点。
直流有源误差
图1 所描述的信号链采用了最普通的构建模块,这是数据采集系统的一种实现方法。该信号链由两个放大器、一个多路复用器和一个 ADC 构成。但要记住的是,有许多类型的有源器件都描述了各类信号链和不同的系统拓扑结构。在实施这类分析时,所有有源器件都会有某些类型的直流误差。为了了解要设计的系统的精度,必须决定要考虑哪些误差,这一点十分重要。
基本而言,直流精度中涉及两类/组误差。对所有这些有源器件来说,这些误差既有个别性,也有普遍性。单个有源器件误差只会显示相对于该器件的已知直流误差。这类误差可以在相应的数据手册里找到。例如,放大器的输入失调电压会被认为属于个别误差,因为此误差只是该有源器件特有的误差。
全局误差是信号链或系统中各个有源器件均存在的等量误差,但根据有源器件各自性能的不同,会表现出不同的误差 (图7)。全局误差的一个例子是总线电源和温度的电压调整率误差。接下来,我们逐一分解信号链中所示三个有源器件的这些误差。
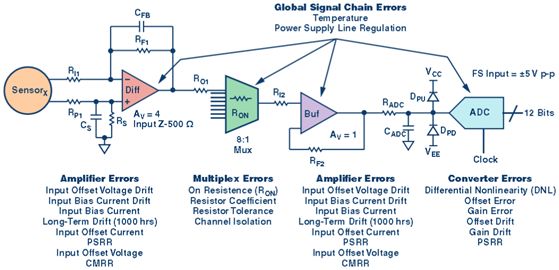
图7. 有源器件受两类直流精度误差的影响—个别误差和全局误差。
表1. 放大器的各种误差
多路复用器的误差一般少于放大器。在各种多路复用器直流误差中,导通电阻和通道隔离是影响最大的误差。表 2 列出了在使用多路复用器时应考虑的误差。
表2. 多路复用器的各种误差

失调、增益和 DNL 都是众所周知且较好理解的误差。同时还要包括PSRR。在使用第一部分提到的 ADC 时,应该考虑下列转换器误差:
- 相对精度DNL,定义为±0.5 LSBs。
- 相对精度温度系数DNL温度系数,通常包含在数据手册的相对精度规格中。
- 增益温度系数误差,为±2.5 LSB (数据来源于上文示例)。
- 失调温度系数误差,为±1.3 LSB (数据来源于上文示例)。
- 电源灵敏度,通常以第一奈奎斯特区内的低频PSRR表示;对于12位ADC而言,一般可表示为60 dB或±2 LSB。
上面就个别有源器件的误差提出了建议并给出了其定义,接下来,应该考虑全局误差,这类误差会对整个信号链产生影响 (表3)。在这个简单的示例中,只会将温度和电压调整率作为全局误差进行分析。然而,同时还有必要考虑特定应用或设计内在的任何其他外部影响因素。
表3. 全局信号链

将器件连接起来
前面定义了全部有源和无源误差,接下来,我们要把这些误差输入电子表格里,以便计算信号链的直流精度。表4展示了完成这一任务的一种方法。
虽然分析信号链精度的方法有许多种,但电子表格法却最为灵活。这种方法还有助于了解如何把所有这些误差数据在信号链设计中进行细分。借助这种方法,设计人员可以快速而有效地在可以为设计考虑的合适器件之间做出权衡。
花些时间编制一份电子表格,使其布局合理、有序。在表格顶部,定义全局误差和信号链规格,因为这些数据会影响整个信号链的性能。放大器规格/误差也放在顶部,因为整个信号链中有多种误差和两个放大器级。
往下,在表格左侧,把所有误差细分到各电阻级。电阻误差也细分到了各个级,以便于了解相应的权衡情况。右侧所示为在信号流进流出各级时连读计算和累计计算的误差。
在计算结果,所有误差均已转换成电压格式。这样是为了方便起见,因为转换器处于信号链末端,其输入满量程是以电压进行描述的。RTO (参考输出)用于描述从一级到下一级连续累计的 误差。各级同时还产生一个独立的合计数和RSS (和方根)合计数,以展示根据所用方法的不同,误差是如何累积起来的。
因此,根据表4里的最终结果,累计的合计误差为±2.6%,RSS误差为±1.6%。这是本文讨论的整个信号链的误差,其前提是针对各个部分的数据手册规格以及前面提到的在26°C下的全局条件。
表4. 全信号链分析示例

累积总量
精度可以通过多种方式计算,并且可能表现为多种形式。根据设计人员的想法,可以深入了解并记录所用方法,以避免形成错误结果。请记住,在第一部分,我们提到,如果只是用所有这些误差源的和方根(RSS)值,结果可能会过于悲观。然而,统计容差结果可能过于乐观了(总误差之和除以误差数)。整个信号链的实际容差应当介于这两种思路或方法之间。
因此,当在整个信号链中加入(累积)精度误差的时候,或者进行任何系统精度分析的时候,设计人员应当使用加权误差源法(如第一部分ADC示例所示),然后对这些误差源进行RSS计算。这是确定整个信号链总误差的最佳方法。
结论
无源和有源器件都会出现多种误差。并非所有误差都很重要,但要记住对信号链应用重要的那些误差。并非所有误差对每种应用都有效。在进行任何直流精度误差分析时,决定最重要或者影响最大或权重最大的误差有哪些,这是必不可少的步骤。
选择合适的无源器件对于信号链中的累积误差就如有源器件一样有用。编制电子表格并对数据进行分类,有助于快速考虑多种不同的器件和折衷情况。最后,误差的累积可能表现为多种不同形式,最常用的方法是RSS精度法。
然而,有人可能认为,加权总和误差法是确定“最差条件直流误差”的正确方式。否则,这可能轻易导致信号链的设计超过规格要求,用更多器件来补偿原来的误差集。更不用说成本及设计大小、重量和功率(SWaP)等因素的增量。
亚德诺半导体



 /5
/5 


