获得一个参数的方法有很多,有的人根据参考设计确定参数,有的人根据别人的推荐确定参数,有的人通过试验确定参数,有的人利用规格书提供的公式计算参数,还有人会考虑不同的工作状态确定参数,到底选用哪一种,与自己的状态、条件和需求密切相关。这个过程越复杂,自己得到的锻炼也越多,看起来是在为难自己,但到了某一天就会发现自己已经进入了自由之境,再也不会为此而烦恼了。
我看过的讲开关电源原理的书(《开关电源的原理与设计》,作者:张占松,蔡宣三,电子工业出版社出版,后面的图片和公式摘自此书,有需要的读者请自行购买阅读)没有给出电感量要如何确定的方法,但是给出了一些比较基本的东西,例如推导占空比的计算公式、输出电压纹波的计算方法,而电感量所起的作用就在其中了,下面摘要分享给大家。
先看原理图:
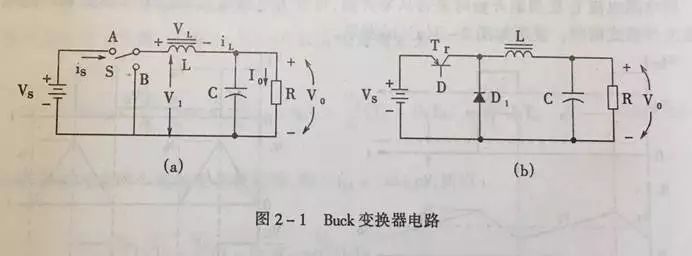

再看波形图:
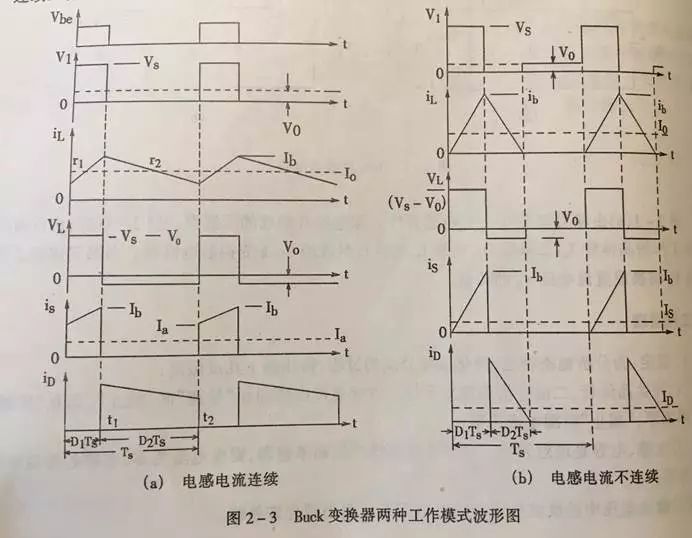
占空比是 Buck 工作中一个很重要的参数,要得到它,需要从一个平衡状态开始进行考虑,这个时候输入与输出之间是平衡的,输入电压是不变的,输出电压也是不变的,转换到电感上,充电阶段和放电阶段的电流变化量也就是相等的。
由于
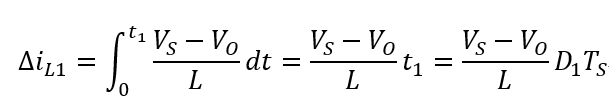
这是上桥开关接通期间电感充电的电流增量计算公式,VS 是输入电压,VO 是输出电压,此两者落在电感两端对其充电;L 是电感量;TS为开关周期;D1 是上桥开关接通时间在一个周期中的占空比,上桥开关从时间 0 开始接通,至时间 t1 截止。
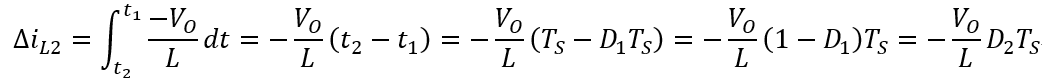
这是上桥开关截止、下桥开关接通期间的电感电流变化量计算公式,此时只有输出电压落在电感上,方向与充电期间的相反,所以电压反映为负值。公式中的 t2 为一个工作周期的结束时间;D2 是上桥截止、下桥导通时间在一个周期中的占空比,它与 D1 合起来为一个周期,所以有 D1+D2=1。因为平衡,一个周期中的电流增量与电流减量是相等的,所以有
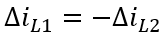
即
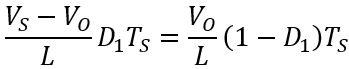
整理后的结果是
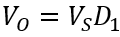
或者是它的变形:
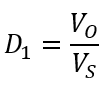
由于 VS 是固定的,所以是 D1 决定了输出电压,而 D1 是占空比。一般的 Buck 器件规格书通常都会给出最大占空比的值,我们根据规格书中的数据和实际的最低输入电压,便知道能够得到的最高输出电压是多少,或者说是反过来,根据最低输入电压、输出电压和最高占空比,我们便知道这款器件是否能够满足我们的要求,这在输入、输出压差很低的场合是很重要的一个考虑因素。
器件规格书通常不会给出最低占空比是多少,但会给出一个最短导通时间的参数,同时会给出一个工作频率的数据,工作频率的倒数即是工作周期 TS,最短导通时间即是上述公式中的 t1 的最小值,它对应着占空比 D1 的最小值。以 RTQ2130B 为例,这是一款工作电压范围为 3V-36V、负载能力 0.7A、工作频率为 2.1MHz±10% 的 Buck 器件,通过了 AEC-Q100 Grade 1 认证,这意味着它可以在非常恶劣的环境条件下(-40℃~125℃)长期可靠地工作,它的规格书是这样来表示这些参数的:

在最高工作频率 2.31MHz 下,一个周期的时长为 TS = 1/2.31MHz = 432.9nS,所以它的最低占空比为 D1min = 60/432.9 = 0.1386 = 13.86%。假如输入电压为 36V,在保持工作频率不变的情形下,最低的输出电压为 36V x 13.86% =4.9896V,要想得到 3.3V 的输出是不可能做到的,只有容许工作频率发生变化,也就是进入 PSM 工作状态,才能输出低于 4.9896V 的电压(这样说比 3.3V 更具有普遍意义)。
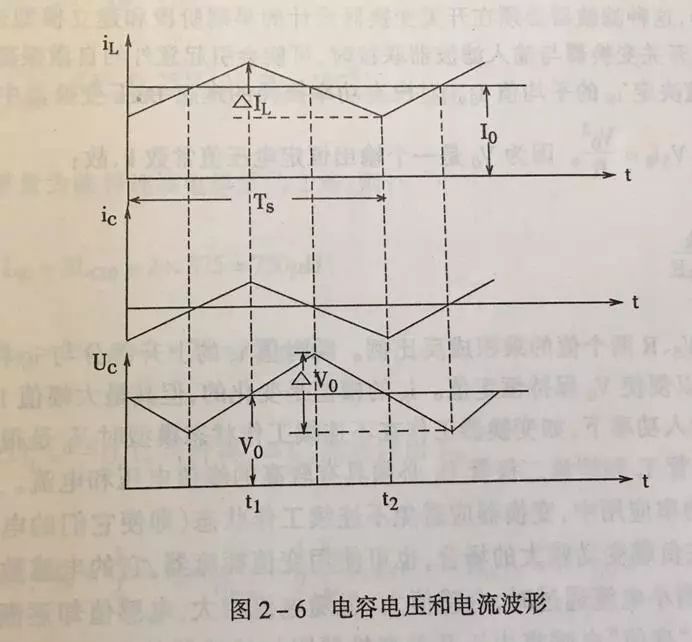
在 Buck 稳定工作期间,电感电流的平均值与负载电流相等,那些高于负载电流的部分将流入输出电容,因而会使输出电压升高;那些低于负载电流的部分就需要电容储能流出来予以弥补,因而会使输出电压降低。在这样的一个周期中,输出电压将要发生用下述公式所表达的变化:
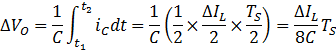
由于

所以有
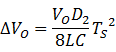
这便是输出电压纹波幅度的计算公式,由此可见:工作频率越高(TS 便越小),输出纹波便越小,而且其影响成平方关系,因此作用最大;电感和输出电容的值都与输出纹波成反比关系;输出电压与输出电压纹波成正比关系。
当一个 Buck 器件已经选定了的时候,它的工作频率通常已经确定;输出电压和占空比则不可能自己选择,应用的环境已经做了决定,自己能够做主的就是 L 和 C 的值,这时候就要根据应用对输出电压纹波的需求进行参数的计算,我们这时候会发现 L 和 C 的作用是同等的,以我来说就会有一种不知所措的感觉,到底是让 C 大一点还是让 L 大一点呢?好在前人已经做过很多的工作,他们发现让电感电流纹波等于负载电流的 20%-40% 是比较好的,这样做能在性能、成本和体积等方面有一个比较好的均衡,于是就可以根据这一数据先把电感量确定下来,但这也只是一个参考而已,你完全可以按照自己的心意去做。如果你记忆力好,自然可以在前面提供的计算公式基础上做点变形,但一般的产品规格书都会给出最简单的做法,以 RTQ2130B 为例,它在规格书的应用说明部分就给出了下述电感计算公式:
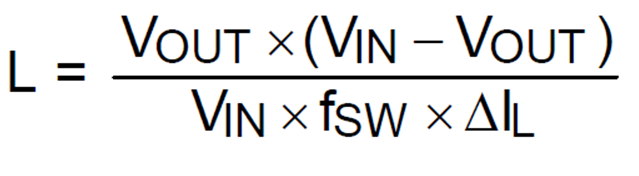
其中的 VOUT 是输出电压,VIN 是输入电压,fSW 是工作频率,
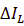
就是电感电流纹波。
到此为止,本文开始提出来的问题就已经解决了,但你还可以做更多的思考。
上述计算公式通常是以最大负载为基础进行计算的,电流纹波的数据在负载降低直至电感电流开始进入连续和非连续的临界状态时都会保持不变,所以输出电压纹波也会保持不变。
如果负载继续降低,电流非连续模式就成为常态,很显然这时候的电感电流纹波是低于连续模式的,所以输出电压纹波一定是低于连续工作模式的。
如果输入电压很高而输出电压很低,这时候有可能出现我们前面提及的 PSM 工作模式,上桥开关的动作不再是周期性连续的,这时候的纹波就与器件的工作模式有关了。如果每一次上桥接通都是以最小导通时间实施,电感的电流纹波就不会比连续工作模式时的更高,这样就不会带来输出电压纹波的增加。如果该转换器是以滞回式模式工作,由于上桥每一次导通的电流都是比较大的,它的输出电压纹波就会比较高,高于连续工作模式时的表现,但这种模式也同时带来别的好处,它的静态耗电会非常低。介于这两种模式之间的情况也可以存在,这就要具体情况具体分析了,我们在选择之前可以做比较深入的研究,避免选择以后再改变就比较痛苦。PSM 模式的最大问题是低频纹波,这个问题超出了今日题目的范畴,在此不做更多探讨。
当我们确定了电感的纹波电流数据以后,流过它的最大电流数据就可以很容易地确定下来,它等于最大输出电流加上纹波电流数据的一半。同时,输出电容的容量也是确定了的,我们可以从前面纹波电压的计算公式得到它,也可以借助规格书来完成:
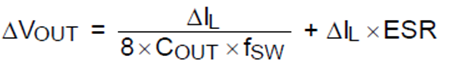
来源: RichtekTechnology







 /2
/2 

