相信网上现在有很多关于FFT的教程,我曾经也参阅了很多网上的教程,感觉都不怎么通俗易懂。在基本上的研究FFT,并且通过编程的形式实现之后。我决定写一篇通俗易懂的关于FFT的讲解。因此我在接下来的叙述中尽量非常通俗细致的讲解。
本人最早知道傅里叶变换的时候是沉迷于音乐的频谱跳动无法自拔,当时就很想做一个音乐频谱显示器。搜阅了很多资料之后,才了解到傅里叶变换,和FFT。当然这都是以前的事情了,经过了系统的学习+2个星期的研究,自制了一个FFT的算法,不敢说速度上的优势,但是个人认为是一种通俗易懂的实现方法。经过实际的VC++模拟实验、和STM32跑的也很成功。
首先,要会FFT,就必须要对DFT有所了解,因为两者之间本质上是一样的。在此之前,先列出离散傅里叶变换对(DFT):
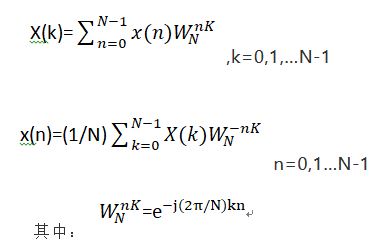
但是FFT之所以称之为快速傅里叶变换,就利用了以下的几个性质(重中之重!)
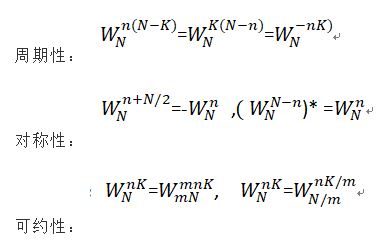
先把这仨公式放到这,接下来会用到。
根据这几个特性,就可以将一个长的DFT运算分解为若干短序列的DFT运算的组合,从而减少运算量。在这里,为了方便理解,我就用了一个按时间抽取的快速傅里叶变换(DIT-FFT)的方法。
首先,将一个序列x(n)一分为二
对于
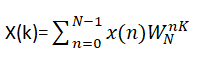
,k=0,1,…N-1 设N是2的整次幂 也就是N=2^M
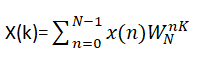
将x(n)按照奇偶分组
x(2r)=x1(r)
x(2r+1)=x2(r) r=0,1,…..(N/2)-1
那么将DFT也分为两组来预算
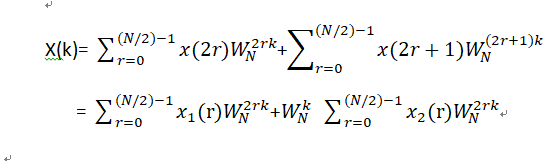
(第一项是偶 第二项是奇)
这个时候,我们上边提的三个性质中的可约性就起到作用了:
回顾一下:
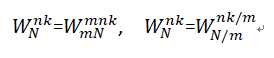
那么这个式子就可以化为:
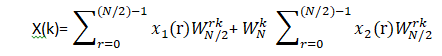
则X1(k)和X2(k)都是长度为N/2的序列 x1(k)和x2(k)的N/2点的离散傅里叶变换
其中:
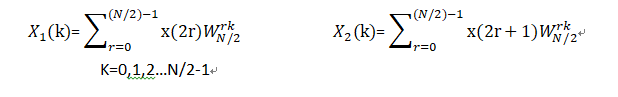
K=0,1,2…N/2-1
至此,一个N点的DFT就被分解为2个N/2的DFT。但是X1(k),和X2(k)只有N/2个点,也就是说式子(1-1)只是DFT前半部分。要求DFT的后半部分可以利用其对称性求出后半部分为:
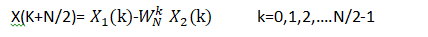
那么式(1-1)和(1-2)就可以专用一个蝶形信号流图符号来表示。如图:
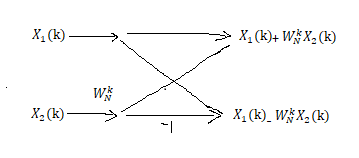
以N=8为例,可以用下图表示:
通过这样的分解,每一个N/2点DFT只需(N^2)/4次复数相乘计算,明显的节省了运算量。
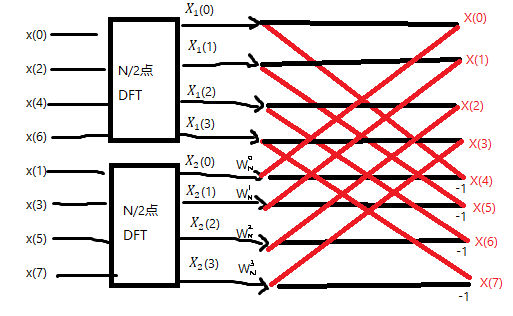
以此类推,继续将已经得出的X1(k)和X2(k)按照奇偶分解,还是和上边一样的方法。那么就得出了百度上都可以找到的一大推的这个图片了。 (笑)
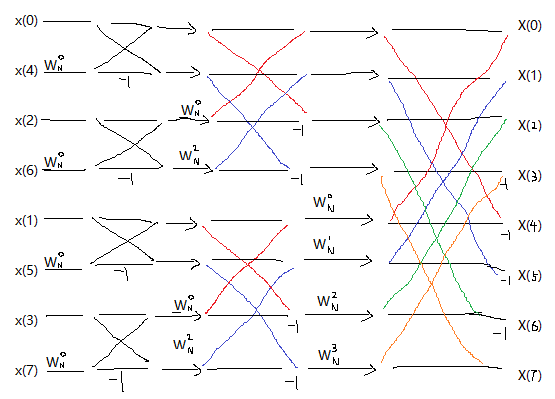
对于这张图片我想强调的一点就是第二阶蝶形运算的时候,WN0之后不应该是WN1吗,为什么是W2N了,这个问题之前困扰了我一段时间,但是不要忘了,前者的 W0N的展开是W0N/2 因为此时N已经按照奇偶分开了,所以是N/2 而W2N/2也就是 W2N是根据可约性得出的,在这里不能混淆.。
对于运算效率就不用多提了
以上就是FFT算法的理论内容了,接下来就是用C语言对这个算法的实现了,对于FFT算法C语言的实现,网上的方法层出不穷,介于本人比较懒(懒得看别人的程序),再加上自给自足丰衣足食的原则,我自己也写了一个个人认为比较通俗易懂的程序,并且为了帮助读者理解,我特意尽量减少了库函数的使用,一些基本的函数都是自己写的(难免有很多BUG),但是作为FFT算法已经够用了,目前这个程序只能处理2^N的数据,理论上来讲如果不够2^N的话可以在后面数列补0这种操作为了简约我也就没有实现,但是主要的功能是具备的,下面是代码:
/* 时间:2018年11月24日 功能:将input里的数据进行快速傅里叶变换 并且输出 */ #include <stdio.h> #include <math.h> #define PI 3.1415926 #define FFT_LENGTH 8 double input[FFT_LENGTH]={1,1,1,1,1,1,1,1}; struct complex1{ //定义一个复数结构体 double real; //实部 double image; //虚部 }; //将input的实数结果存放为复数 struct complex1 result_dat[8]; /* 虚数的乘法 */ struct complex1 con_complex(struct complex1 a,struct complex1 b){ struct complex1 temp; temp.real=(a.real*b.real)-(a.image*b.image); temp.image=(a.image*b.real)+(a.real*b.image); return temp; } /* 简单的a的b次方 */ int mypow(int a,int b){ int i,sum=a; if(b==0)return 1; for(i=1;i<b;i++){ sum*=a; } return sum; } /* 简单的求以2为底的正整数 */ int log2(int n){ unsigned i=1; int sum=1; for(i;;i++){ sum*=2; if(sum>=n)break; } return i; } /* 简单的交换数据的函数 */ void swap(struct complex1 *a,struct complex1 *b){ struct complex1 temp; temp=*a; *a=*b; *b=temp; } /* dat为输入数据的数组 N为抽样次数 也代表周期 必须是2^N次方 */ void fft(struct complex1 dat[],unsigned char N){ /*最终 dat_buf计算出 当前蝶形运算奇数项与W 乘积 dat_org存放上一个偶数项的值 */ struct complex1 dat_buf,dat_org; /* L为几级蝶形运算 也代表了2进制的位数 n为当前级蝶形的需要次数 n最初为N/2 每级蝶形运算后都要/2 i j为倒位时要用到的自增符号 同时 i也用到了L碟级数 j是计算当前碟级的计算次数 re_i i_copy均是倒位时用到的变量 k为当前碟级 cos(2*pi/N*k)的 k 也是e^(-j2*pi/N)*k 的 k */ unsigned char L,i,j,re_i=0,i_copy=0,k=0,fft_flag=1; //经过观察,发现每级蝶形运算需要N/2次运算,共运算N/2*log2N 次 unsigned char fft_counter=0; //在此要进行补2 N必须是2^n 在此略 //蝶形级数 (L级) L=log2(N); //计算每级蝶形计算的次数(这里只是一个初始值) 之后每次要/2 //n=N/2; //对dat的顺序进行倒位 for(i=1;i<N/2;i++){ i_copy=i; re_i=0; for(j=L-1;j>0;j--){ //判断i的副本最低位的数字 并且移动到最高位 次高位 .. //re_i为交换的数 每次它的数字是不能移动的 并且循环之后要清0 re_i|=((i_copy&0x01)<<j); i_copy>>=1; } swap(&dat[i],&dat[re_i]); } //进行fft计算 for(i=0;i<L;i++){ fft_flag=1; fft_counter=0; for(j=0;j<N;j++){ if(fft_counter==mypow(2,i)){ //控制隔几次,运算几次, fft_flag=0; }else if(fft_counter==0){ //休止结束,继续运算 fft_flag=1; } //当不判断这个语句的时候 fft_flag保持 这样就可以持续运算了 if(fft_flag){ dat_buf.real=cos((2*PI*k)/(N/mypow(2,L-i-1))); dat_buf.image=-sin((2*PI*k)/(N/mypow(2,L-i-1))); dat_buf=con_complex(dat[j+mypow(2,i)],dat_buf); //计算 当前蝶形运算奇数项与W 乘积 dat_org.real=dat[j].real; dat_org.image=dat[j].image; //暂存 dat[j].real=dat_org.real+dat_buf.real; dat[j].image=dat_org.image+dat_buf.image; //实部加实部 虚部加虚部 dat[j+mypow(2,i)].real=dat_org.real-dat_buf.real; dat[j+mypow(2,i)].image=dat_org.image-dat_buf.image; //实部减实部 虚部减虚部 k++; fft_counter++; }else{ fft_counter--; //运算几次,就休止几次 k=0; } } } } void main(){ int i; //先将输入信号转换成复数 for(i=0;i<FFT_LENGTH;i++){ result_dat[i].image=0; //输入信号是二维的,暂时不存在复数 result_dat[i].real=input[i]; //result_dat[i].real=10; //输入信号都为实数 } fft(result_dat,FFT_LENGTH); for(i=0;i<FFT_LENGTH;i++){ input[i]=sqrt(result_dat[i].real*result_dat[i].real+result_dat[i].image*result_dat[i].image); //取模 printf("%lf\n",input[i]); } while(1); }
复制代码这就是本次浅谈FFT以及FFT算法的基本实现的全部内容了
原创内容转载其注明原作者.
参考书籍:数字信号处理
来源:21ic论坛,作者:enderman1






 /1
/1 

