高斯滤波器是一种线性滤波器，能够有效的抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1；而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。
什么是高斯滤波器
既然名称为高斯滤波器，那么其和高斯分布（正态分布）是有一定的关系的。一个二维的高斯函数如下：
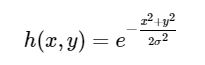其中 ( x , y ) 为点坐标，在图像处理中可认为是整数；σ 是标准差。要想得到一个高斯滤波器的模板，可以对高斯函数进行离散化，得到的高斯函数值作为模板的系数。例如：要产生一个 3×3 的高斯滤波器模板，以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标，如下所示（x轴水平向右，y轴竖直向下）
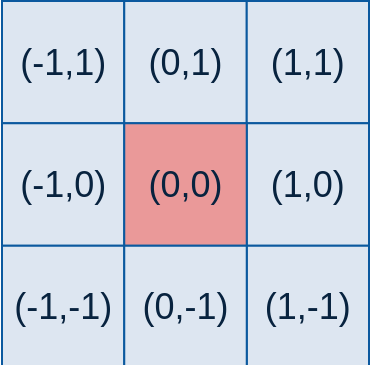这样，将各个位置的坐标带入到高斯函数中，得到的值就是模板的系数。对于窗口模板的大小为 ( 2k + 1 ) × ( 2k + 1 )，模板中各个元素值的计算公式如下：
这样计算出来的模板有两种形式：小数和整数。• 小数形式的模板，就是直接计算得到的值，没有经过任何的处理；
• 整数形式的，则需要进行归一化处理，将模板左上角的值归一化为1，下面会具体介绍。使用整数的模板时，需要在模板的前面加一个系数，系数为
，也就是模板系数和的倒数。高斯模板的生成
知道模板生成的原理，实现起来也就不困难了
void generateGaussianTemplate(double window[][11], int ksize, double sigma){ static const double pi = 3.1415926; int center = ksize / 2; // 模板的中心位置，也就是坐标的原点 double x2, y2; for (int i = 0; i < ksize; i++) { x2 = pow(i - center, 2); for (int j = 0; j < ksize; j++) { y2 = pow(j - center, 2); double g = exp(-(x2 + y2) / (2 * sigma * sigma)); g /= 2 * pi * sigma; window[i][j] = g; } } double k = 1 / window[0][0]; // 将左上角的系数归一化为1 for (int i = 0; i < ksize; i++) { for (int j = 0; j < ksize; j++) { window[i][j] *= k; } } }
复制代码生成的过程，首先根据模板的大小，找到模板的中心位置 ksize/2。 然后就是遍历，根据高斯分布的函数，计算模板中每个系数的值。
需要注意的是，最后归一化的过程，使用模板左上角的系数的倒数作为归一化的系数（左上角的系数值被归一化为1），模板中的每个系数都乘以该值（左上角系数的倒数），然后将得到的值取整，就得到了整数型的高斯滤波器模板。
下面截图生成的是，大小为 3 × 3, σ = 0.8 的模板
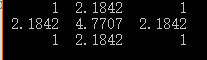对上述解结果取整后得到如下模板：
这个模板就比较熟悉了，其就是根据 σ = 0.8 的高斯函数生成的模板。至于小数形式的生成也比较简单，去掉归一化的过程，并且在求解过程后，模板的每个系数要除以所有系数的和。具体代码如下：void generateGaussianTemplate(double window[][11], int ksize, double sigma){ static const double pi = 3.1415926; int center = ksize / 2; // 模板的中心位置，也就是坐标的原点 double x2, y2; double sum = 0; for (int i = 0; i < ksize; i++) { x2 = pow(i - center, 2); for (int j = 0; j < ksize; j++) { y2 = pow(j - center, 2); double g = exp(-(x2 + y2) / (2 * sigma * sigma)); g /= 2 * pi * sigma; sum += g; window[i][j] = g; } } //double k = 1 / window[0][0]; // 将左上角的系数归一化为1 for (int i = 0; i < ksize; i++) { for (int j = 0; j < ksize; j++) { window[i][j] /= sum; } } }
复制代码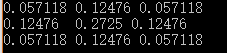
σ 值的意义及选取通过上述的实现过程，不难发现，高斯滤波器模板的生成最重要的参数就是高斯分布的标准差σσ。标准差代表着数据的离散程度，如果σσ较小，那么生成的模板的中心系数较大，而周围的系数较小，这样对图像的平滑效果就不是很明显；反之，σσ较大，则生成的模板的各个系数相差就不是很大，比较类似均值模板，对图像的平滑效果比较明显。
来看下一维高斯分布的概率分布密度图：
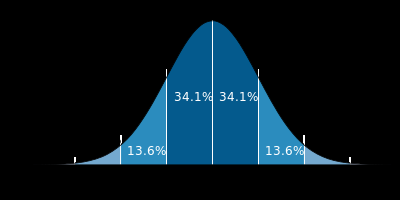横轴表示可能得取值x，竖轴表示概率分布密度F(x)，那么不难理解这样一个曲线与x轴围成的图形面积为1。σσ（标准差）决定了这个图形的宽度，可以得出这样的结论：σσ越大，则图形越宽，尖峰越小，图形较为平缓；σσ越小，则图形越窄，越集中，中间部分也就越尖，图形变化比较剧烈。这其实很好理解，如果sigma也就是标准差越大，则表示该密度分布一定比较分散，由于面积为1，于是尖峰部分减小，宽度越宽（分布越分散）；同理，当σσ越小时，说明密度分布较为集中，于是尖峰越尖，宽度越窄！于是可以得到如下结论：
σσ越大，分布越分散，各部分比重差别不大，于是生成的模板各元素值差别不大，类似于平均模板；
σσ越小，分布越集中，中间部分所占比重远远高于其他部分，反映到高斯模板上就是中心元素值远远大于其他元素值，于是自然而然就相当于中间值得点运算。
基于OpenCV的实现
在生成高斯模板好，其简单的实现和其他的空间滤波器没有区别，具体代码如下：
void GaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma){ CV_Assert(src.channels() || src.channels() == 3); // 只处理单通道或者三通道图像 const static double pi = 3.1415926; // 根据窗口大小和sigma生成高斯滤波器模板 // 申请一个二维数组，存放生成的高斯模板矩阵 double **templateMatrix = new double*[ksize]; for (int i = 0; i < ksize; i++) templateMatrix[i] = new double[ksize]; int origin = ksize / 2; // 以模板的中心为原点 double x2, y2; double sum = 0; for (int i = 0; i < ksize; i++) { x2 = pow(i - origin, 2); for (int j = 0; j < ksize; j++) { y2 = pow(j - origin, 2); // 高斯函数前的常数可以不用计算，会在归一化的过程中给消去 double g = exp(-(x2 + y2) / (2 * sigma * sigma)); sum += g; templateMatrix[i][j] = g; } } for (int i = 0; i < ksize; i++) { for (int j = 0; j < ksize; j++) { templateMatrix[i][j] /= sum; cout << templateMatrix[i][j] << " "; } cout << endl; } // 将模板应用到图像中 int border = ksize / 2; copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT); int channels = dst.channels(); int rows = dst.rows - border; int cols = dst.cols - border; for (int i = border; i < rows; i++) { for (int j = border; j < cols; j++) { double sum[3] = { 0 }; for (int a = -border; a <= border; a++) { for (int b = -border; b <= border; b++) { if (channels == 1) { sum[0] += templateMatrix[border + a][border + b] * dst.at<uchar>(i + a, j + b); } else if (channels == 3) { Vec3b rgb = dst.at<Vec3b>(i + a, j + b); auto k = templateMatrix[border + a][border + b]; sum[0] += k * rgb[0]; sum[1] += k * rgb[1]; sum[2] += k * rgb[2]; } } } for (int k = 0; k < channels; k++) { if (sum[k] < 0) sum[k] = 0; else if (sum[k] > 255) sum[k] = 255; } if (channels == 1) dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]); else if (channels == 3) { Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) }; dst.at<Vec3b>(i, j) = rgb; } } } // 释放模板数组 for (int i = 0; i < ksize; i++) delete[] templateMatrix[i]; delete[] templateMatrix; }
复制代码分离实现高斯滤波
由于高斯函数的可分离性，尺寸较大的高斯滤波器可以分成两步进行：首先将图像在水平（竖直）方向与一维高斯函数进行卷积；然后将卷积后的结果在竖直（水平）方向使用相同的一维高斯函数得到的模板进行卷积运算。具体实现代码如下：
// 分离的计算void separateGaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma) { CV_Assert(src.channels()==1 || src.channels() == 3); // 只处理单通道或者三通道图像 // 生成一维的高斯滤波模板 double *matrix = new double[ksize]; double sum = 0; int origin = ksize / 2; for (int i = 0; i < ksize; i++) { // 高斯函数前的常数可以不用计算，会在归一化的过程中给消去 double g = exp(-(i - origin) * (i - origin) / (2 * sigma * sigma)); sum += g; matrix[i] = g; } // 归一化 for (int i = 0; i < ksize; i++) matrix[i] /= sum; // 将模板应用到图像中 int border = ksize / 2; copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT); int channels = dst.channels(); int rows = dst.rows - border; int cols = dst.cols - border; // 水平方向 for (int i = border; i < rows; i++) { for (int j = border; j < cols; j++) { double sum[3] = { 0 }; for (int k = -border; k <= border; k++) { if (channels == 1) { sum[0] += matrix[border + k] * dst.at<uchar>(i, j + k); // 行不变，列变化；先做水平方向的卷积 } else if (channels == 3) { Vec3b rgb = dst.at<Vec3b>(i, j + k); sum[0] += matrix[border + k] * rgb[0]; sum[1] += matrix[border + k] * rgb[1]; sum[2] += matrix[border + k] * rgb[2]; } } for (int k = 0; k < channels; k++) { if (sum[k] < 0) sum[k] = 0; else if (sum[k] > 255) sum[k] = 255; } if (channels == 1) dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]); else if (channels == 3) { Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) }; dst.at<Vec3b>(i, j) = rgb; } } } // 竖直方向 for (int i = border; i < rows; i++) { for (int j = border; j < cols; j++) { double sum[3] = { 0 }; for (int k = -border; k <= border; k++) { if (channels == 1) { sum[0] += matrix[border + k] * dst.at<uchar>(i + k, j); // 列不变，行变化；竖直方向的卷积 } else if (channels == 3) { Vec3b rgb = dst.at<Vec3b>(i + k, j); sum[0] += matrix[border + k] * rgb[0]; sum[1] += matrix[border + k] * rgb[1]; sum[2] += matrix[border + k] * rgb[2]; } } for (int k = 0; k < channels; k++) { if (sum[k] < 0) sum[k] = 0; else if (sum[k] > 255) sum[k] = 255; } if (channels == 1) dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]); else if (channels == 3) { Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) }; dst.at<Vec3b>(i, j) = rgb; } } } delete[] matrix; }
复制代码在 OpenCV 也有对高斯滤波器的封装 GaussianBlur，其声明如下：
CV_EXPORTS_W void GaussianBlur( InputArray src, OutputArray dst, Size ksize, double sigmaX, double sigmaY = 0, int borderType = BORDER_DEFAULT );
复制代码下图是自己实现的高斯滤波器和OpenCV中的GaussianBlur的结果对比
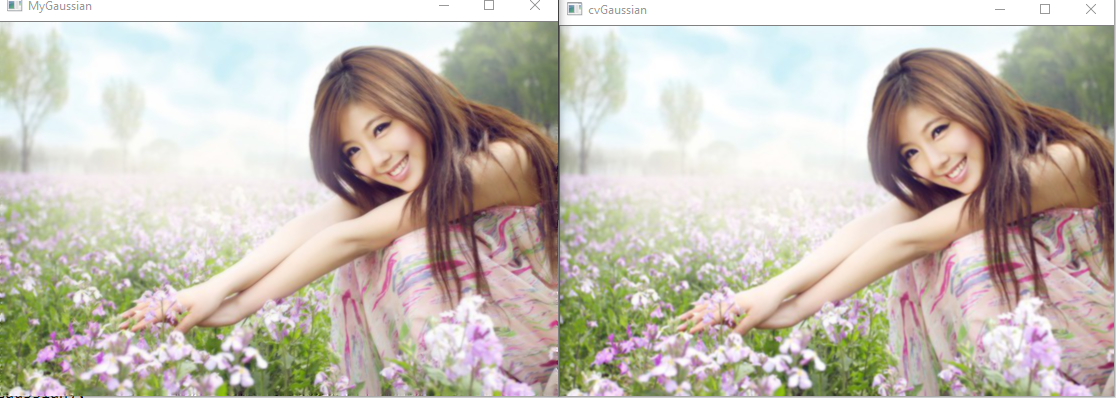上图是 5 × 5 , σ = 0.8 的高斯滤波器，可以看出两个实现得到的结果没有很大的区别。总结
高斯滤波器是一种线性平滑滤波器，其滤波器的模板是对二维高斯函数离散得到。由于高斯模板的中心值最大，四周逐渐减小，其滤波后的结果相对于均值滤波器来说更好。
高斯滤波器最重要的参数就是高斯分布的标准差 σ，标准差和高斯滤波器的平滑能力有很大的能力，σ 越大，高斯滤波器的频带就较宽，对图像的平滑程度就越好。通过调节 σ 参数，可以平衡对图像的噪声的抑制和对图像的模糊。
作者：Brook_icv
原文链接：https://www.cnblogs.com/wangguchangqing/p/6407717.html
/3 
