在某一个频点匹配很容易,但是双频以上就复杂点了。因为在900M完全匹配了,那么1800处就不会达到匹配,要算一个适合的匹配电路。最好用仿真软件或一个点匹配好了,在网络分析仪上 的S11参数下调整,因为双频的匹配点肯定离此处不会太远,只有两个元件匹配是唯一的,但是pi 型网络匹配,就有无数个解了。这时候需要仿真来挑,最好使用经验。
仿真工具在实际过程中几乎没什么用处。因为仿真工具是不知道你元件的模型的。你必须要输入实际元件的模型,也就是说各种分布参数,你的结果才可能与实际相符。一个实际电感器并不是简单用电感量能衡量的,应该是一个等效网络来模拟。本人通常只会用仿真工具做一些理论的研究。
实际设计中,要充分明白Smith圆图的原理,然后用网络分析仪的圆图工具多调试。懂原理让你定性地知道要用什么件,多调是要让你熟悉你所用的元件会在实际的圆图上怎么移动。(由于分布参数及元件的频率响应特性的不同,实际件在圆图上的移动和你理论计算的移动会不同的)。
双频的匹配的确是一个折衷的过程。你加一个件一定是有目的性的。以GSM、DCS双频来说,你如果想调GSM而又不太想改变DCS,你就应该选择串连电容、并联电感的方式。同样如果想调DCS,你应该选择串电感、并电容。
理论上需要2各件调一个频点,所以实际的手机或者移动终端通常按如下规律安排匹配电路:对于简单一些的,天线空间比较大,反射本来就较小的,采用Pai型(2并一串),如常规直板手机、常规翻盖机;稍微复杂些的采用双L型(2串2并):对于更复杂的,采用L+Pai型(2串3并),比如用拉杆天线的手机。
记住,匹配电路虽然能降低反射,但同时会引入损耗。有些情况,虽然驻波比好了,但天线系统的效率反而会降低。所以匹配电路的设计是有些忌讳的;比如在GSM、DCS手机中匹配电路中,串联电感一般不大于5.6nH。还有,当天线的反射本身比较大,带宽不够,在smith图上看到各频带边界点离圆心的半径很大,一般加匹配是不能改善辐射的。
天线的反射指标(VSWR,return loss)在设计过程中一般只要作为参考。关键参数是传输性参数(如效率,增益等)。有人一味强调return loss,一张口要-10dB,驻波比要小于1.5,其实没有意义。我碰到这种人,我就开玩笑说,你只要反射指标好,我给你接一个50欧姆的匹配电阻好了,那样驻波小于1.1啊,至于你手机能不能工作我就不管了!
SWR驻波比仅仅说明端口的匹配程度,即阻抗匹配程度。匹配好,SWR小,天线输入端口处反射回去的功率小。匹配不好,反射回去的功率就大。至于进入天线的那部分功率是不是辐射了,你根本不清楚。天线的效率是辐射到空间的总功率与输入端口处的总功率之比。所以SWR好了,无法判断天线效率一定就高(拿一个50ohm的匹配电阻接上,SWR很好的,但有辐射吗?)。但是SWR不好了,反射的功率大,可以肯定天线的效率一定不会高。SWR好是天线效率好的必要条件而非充分条件。SWR好并且辐射效率(radiation efficiency)高是天线效率高的充分必要条件。当SWR为理想值(1)时,端口理想匹配,此时天线效率就等于辐射效率。
当今的手机,天线的空间压缩得越来越小,是牺牲天线的性能作为代价的。对于某些多频天线,甚至VSWR达到了6。以前大家比较多采用外置天线,平均效率在50%算低的,现在50%以上的效率就算很好了!看一看市场上的手机,即使是名公司的,如Nokia等,也有效率低于20%的。有的手机(滑盖的啊,旋转的啊)甚至在某些频点的效率只有10%左右。
见过几个手机内置天线的测试报告,天线效率基本都在30-40%左右,当时觉得实在是够差的(比我设计的微带天线而言),现在看来还是凑合的了。不过实际工程中,好像都把由于S11造成的损耗和匹配电路的损耗计在效率当中了,按天线原理,只有介质损耗(包括基板引起的和手机内磁铁引起的)和金属损耗(尽管很小)是在天线损耗中的,而回损和匹配电路的损耗不应该记入的。不过工程就是工程啊,这样容易测试啊。
对了,再补充一句,软件仿真在一定程度上是对工程有帮助的:当然,仿真的结果准确程度没法跟测试相比,但是通过参数扫描仿真获取的天线性能随参数变化趋势还是有用的,这比通过测试获取数据要快不少,尤其是对某些不常用的参数。
“仿真工具在实际工程中没有什么用处”,是说在设计匹配电路时,更具体一点是指设计双频GSM、DCS手机天线匹配电路时。如果单独理解这句话,无疑是错的。事实上,我一直在用HFSS进行天线仿真,其结果也都是基于仿真结果的。
对了,焊元器件真的是一件费劲的事,而且也有方法的,所谓熟能生巧嘛。大的公司可能给你专门配焊接员,那样你可能就只要说焊什么就可以了。然而,我们在此讨论的是如何有效地完成匹配电路的设计。注意有效性!有效性包括所耗的时间以及选择元器件的准确性。如果没有实际动手的经验,只通过软件仿真得出一种匹配设计然而用到实际天线输入端。呵呵,我可以说,十有八九你的设计会不能用,甚至和你的想象大相径庭!
实际设计中,还有一种情况你在仿真中是无法考虑的(除非你事先测量)。那就是,分布参数对于PIFA的影响。由于如今天线高度越来越小,而匹配电路要么在天线的下方(里面)要么在其下方(外面),反正很近,加入一个实际元件在实际中会引入分布参数的改变。尤其如果电路板排版不好,这种效应会明显一些。实际焊接时,甚至如果一个件焊得不太好,重新焊接一下,都会带来阻抗的变化。
所以,PIFA的设计中,通常我们不采用匹配电路(或者叫0ohm匹配)。这就要求你仔细调节优化你的天线。一般来说对现今的柔性电路板设计方案(Flexfilm)比较容易做到,因为修改辐射片比较容易。对于用得比较多的另一种设计方案冲压金属片(stamping metal),相对来说就比较难些了。一是硬度大,受工艺的限制不能充分理由所有空间,二是模具一旦成型要多次修改辐射片的设计也很困难。
在匹配设计上仿真工具有没有很大的用处,没多少人是可以用仿真工具算出匹配来的。再说,有没有很大效果怎么衡量呢? 工程上讲究的是快速,准确。为了仿真而仿真,没有实际意义。为了得到一个2、3、最多5个件的匹配你去建立电感、电容的模型,不太值的。还有,你如何考虑上面我提到的PIFA匹配的分布参数的改变?前面我还说到一些匹配电路的忌讳,不是源于理论,完全源于实践。因为天线的设计是希望能提高它的辐射效率(总效率)!我没有成功地在1小时内通过仿真工具找到过准确的匹配电路(就说GSM、DCS)双频的吧,(实际中用视错法是可以的)。
在处理RF系统的实际应用问题时,总会遇到一些非常困难的工作,对各部分级联电路的不同阻抗进行匹配就是其中之一。一般情况下,需要进行匹配的电路包括天线与低噪声放大器(LNA)之间的匹配、功率放大器输出(RFOUT)与天线之间的匹配、LNA/VCO输出与混频器输入之间的匹配。匹配的目的是为了保证信号或能量有效地从“信号源”传送到“负载”。
在高频端,寄生元件(比如连线上的电感、板层之间的电容和导体的电阻)对匹配网络具有明显的、不可预知的影响。频率在数十兆赫兹以上时,理论计算和仿真已经远远不能满足要求,为了得到适当的最终结果,还必须考虑在实验室中进行的RF测试、并进行适当调谐。需要用计算值确定电路的结构类型和相应的目标元件值。
有很多种阻抗匹配的方法,包括
· 计算机仿真: 由于这类软件是为不同功能设计的而不只是用于阻抗匹配,所以使用起来比较复杂。设计者必须熟悉用正确的格式输入众多的数据。设计人员还需要具有从大量的输出结果中找到有用数据的技能。另外,除非计算机是专门为这个用途制造的,否则电路仿真软件不可能预装在计算机上。
· 手工计算: 这是一种极其繁琐的方法,因为需要用到较长(“几公里”)的计算公式、并且被处理的数据多为复数。
· 经验: 只有在RF领域工作过多年的人才能使用这种方法。总之,它只适合于资深的专家。
· 史密斯圆图:本文要重点讨论的内容。
本文的主要目的是复习史密斯圆图的结构和背景知识,并且总结它在实际中的应用方法。讨论的主题包括参数的实际范例,比如找出匹配网络元件的数值。当然,史密斯圆图不仅能够为我们找出最大功率传输的匹配网络,还能帮助设计者优化噪声系数,确定品质因数的影响以及进行稳定性分析。
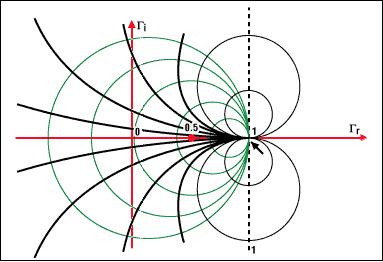
图1. 阻抗和史密斯圆图基础
基础知识在介绍史密斯圆图的使用之前,最好回顾一下RF环境下(大于100MHz) IC连线的电磁波传播现象。这对RS-485传输线、PA和天线之间的连接、LNA和下变频器/混频器之间的连接等应用都是有效的。
大家都知道,要使信号源传送到负载的功率最大,信号源阻抗必须等于负载的共轭阻抗,即:
RS + jXS = RL - jXL
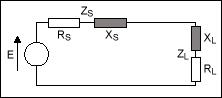
图2. 表达式RS + jXS = RL - jXL的等效图
在这个条件下,从信号源到负载传输的能量最大。另外,为有效传输功率,满足这个条件可以避免能量从负载反射到信号源,尤其是在诸如视频传输、RF或微波网络的高频应用环境更是如此。史密斯圆图
史密斯圆图是由很多圆周交织在一起的一个图。正确的使用它,可以在不作任何计算的前提下得到一个表面上看非常复杂的系统的匹配阻抗,唯一需要作的就是沿着圆周线读取并跟踪数据。
史密斯圆图是反射系数(伽马,以符号Γ表示)的极座标图。反射系数也可以从数学上定义为单端口散射参数,即s11。
史密斯圆图是通过验证阻抗匹配的负载产生的。这里我们不直接考虑阻抗,而是用反射系数ΓL,反射系数可以反映负载的特性(如导纳、增益、跨导),在处理RF频率的问题时ΓL更加有用。
我们知道反射系数定义为反射波电压与入射波电压之比:
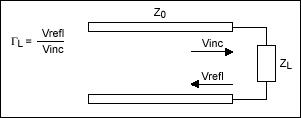
图3. 负载阻抗
负载反射信号的强度取决于信号源阻抗与负载阻抗的失配程度。反射系数的表达式定义为:
由于阻抗是复数,反射系数也是复数。
为了减少未知参数的数量,可以固化一个经常出现并且在应用中经常使用的参数。这里Z0 (特性阻抗)通常为常数并且是实数,是常用的归一化标准值,如50Ω、75Ω、100Ω和600Ω。于是我们可以定义归一化的负载阻抗:

据此,将反射系数的公式重新写为:
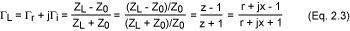
从上式我们可以看到负载阻抗与其反射系数间的直接关系。但是这个关系式是一个复数,所以并不实用。我们可以把史密斯圆图当作上述方程的图形表示。
为了建立圆图,方程必需重新整理以符合标准几何图形的形式(如圆或射线)。
首先,由方程2.3求解出;

并且

令等式2.5的实部和虚部相等,得到两个独立的关系式:

重新整理等式2.6,经过等式2.8至2.13得到最终的方程2.14。这个方程是在复平面(Γr,Γi)上、圆的参数方程(x - a)² + (y - b)² = R²,它以[r/(r + 1),0]为圆心,半径为1/(1 + r)。
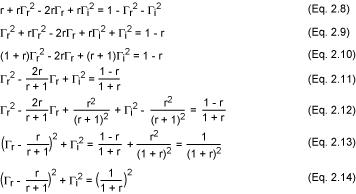
更多细节参见图4a。
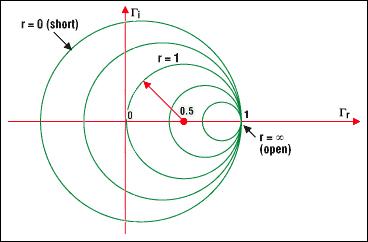
在作史密斯圆图时,有一些需要注意的问题。下面是最重要的几个方面:
· 所有的圆周只有一个相同的,唯一的交点(1,0)。
· 代表0Ω、也就是没有电阻(r = 0)的圆是最大的圆。
· 无限大的电阻对应的圆退化为一个点(1,0)
· 实际中没有负的电阻,如果出现负阻值,有可能产生振荡。
· 选择一个对应于新电阻值的圆周就等于选择了一个新的电阻。
作图
经过等式2.15至2.18的变换,2.7式可以推导出另一个参数方程,方程2.19。
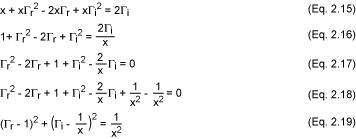
同样,2.19也是在复平面(Γr,Γi)上的圆的参数方程(x - a)² + (y - b)² = R²,它的圆心为(1,1/x),半径1/x。
更多细节参见图4b。
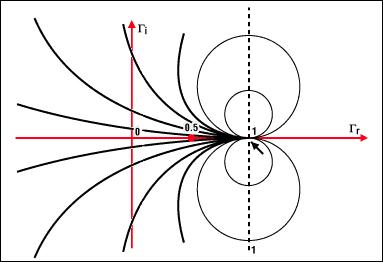
完成圆图
为了完成史密斯圆图,我们将两簇圆周放在一起。可以发现一簇圆周的所有圆会与另一簇圆周的所有圆相交。若已知阻抗为r + jx,只需要找到对应于r和x的两个圆周的交点就可以得到相应的反射系数。
可互换性
上述过程是可逆的,如果已知反射系数,可以找到两个圆周的交点从而读取相应的r和×的值。过程如下:
· 确定阻抗在史密斯圆图上的对应点
· 找到与此阻抗对应的反射系数(Γ)
· 已知特性阻抗和Γ,找出阻抗
· 将阻抗转换为导纳
· 找出等效的阻抗
· 找出与反射系数对应的元件值(尤其是匹配网络的元件,见图7)
推论
因为史密斯圆图是一种基于图形的解法,所得结果的精确度直接依赖于图形的精度。下面是一个用史密斯圆图表示的RF应用实例:
例: 已知特性阻抗为50Ω,负载阻抗如下:
| Z1 = 100 + j50Ω | Z2 = 75 - j100Ω | Z3 = j200Ω | Z4 = 150Ω |
| Z5 = ∞ (an open circuit) | Z6 = 0 (a short circuit) | Z7 = 50Ω | Z8 = 184 - j900Ω |
| z1 = 2 + j | z2 = 1.5 - j2 | z3 = j4 | z4 = 3 |
| z5 = 8 | z6 = 0 | z7 = 1 | z8 = 3.68 - j18 |
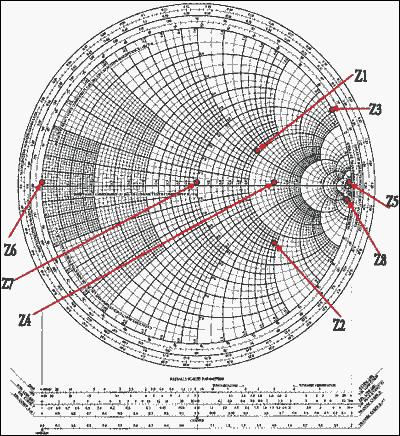
图5. 史密斯圆图上的点
现在可以通过图5的圆图直接解出反射系数Γ。画出阻抗点(等阻抗圆和等电抗圆的交点),只要读出它们在直角坐标水平轴和垂直轴上的投影,就得到了反射系数的实部Γr和虚部Γi (见图6)。该范例中可能存在八种情况,在图6所示史密斯圆图上可以直接得到对应的反射系数Γ:
| Γ1 = 0.4 + 0.2j | Γ2 = 0.51 - 0.4j | Γ3 = 0.875 + 0.48j | Γ4 = 0.5 |
| Γ5 = 1 | Γ6 = -1 | Γ7 = 0 | Γ8 = 0.96 - 0.1j |
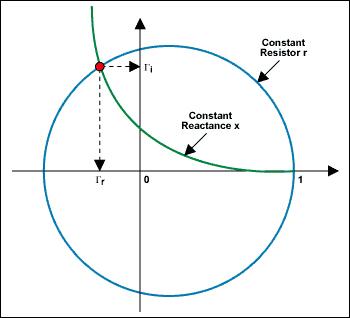
图6. 从X-Y轴直接读出反射系数Γ的实部和虚部
用导纳表示史密斯圆图是用阻抗(电阻和电抗)建立的。一旦作出了史密斯圆图,就可以用它分析串联和并联情况下的参数。可以添加新的串联元件,确定新增元件的影响只需沿着圆周移动到它们相应的数值即可。然而,增加并联元件时分析过程就不是这么简单了,需要考虑其它的参数。通常,利用导纳更容易处理并联元件。
我们知道,根据定义Y = 1/Z,Z = 1/Y。导纳的单位是姆欧或者Ω-1 (早些时候导纳的单位是西门子或S)。并且,如果Z是复数,则Y也一定是复数。
所以Y = G + jB (2.20),其中G叫作元件的“电导”,B称“电纳”。在演算的时候应该小心谨慎,按照似乎合乎逻辑的假设,可以得出:G = 1/R及B = 1/X,然而实际情况并非如此,这样计算会导致结果错误。
用导纳表示时,第一件要做的事是归一化,y = Y/Y0,得出y = g + jb。但是如何计算反射系数呢?通过下面的式子进行推导:
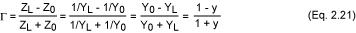
结果是G的表达式符号与z相反,并有Γ(y) = -Γ(z)。
如果知道z,就能通过将的符号取反找到一个与(0,0)的距离相等但在反方向的点。围绕原点旋转180°可以得到同样的结果(见图7)。
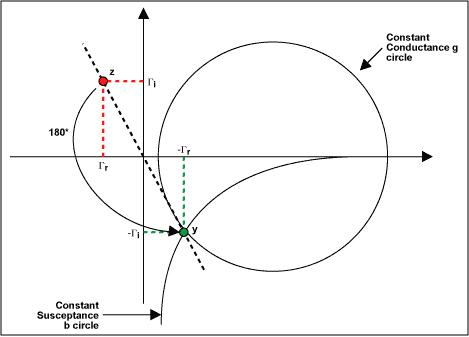
图7. 180°度旋转后的结果
当然,表面上看新的点好像是一个不同的阻抗,实际上Z和1/Z表示的是同一个元件。(在史密斯圆图上,不同的值对应不同的点并具有不同的反射系数,依次类推)出现这种情况的原因是我们的图形本身是一个阻抗图,而新的点代表的是一个导纳。因此在圆图上读出的数值单位是西门子。尽管用这种方法就可以进行转换,但是在解决很多并联元件电路的问题时仍不适用。
导纳圆图
在前面的讨论中,我们看到阻抗圆图上的每一个点都可以通过以Γ复平面原点为中心旋转180°后得到与之对应的导纳点。于是,将整个阻抗圆图旋转180°就得到了导纳圆图。这种方法十分方便,它使我们不用建立一个新图。所有圆周的交点(等电导圆和等电纳圆)自然出现在点(-1,0)。使用导纳圆图,使得添加并联元件变得很容易。在数学上,导纳圆图由下面的公式构造:

解这个方程:

接下来,令方程3.3的实部和虚部相等,我们得到两个新的独立的关系:

从等式3.4,我们可以推导出下面的式子:
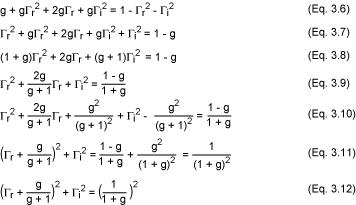
它也是复平面(Γr,Γi)上圆的参数方程(x - a)² + (y - b)² = R² (方程3.12),以[g/(g + 1),0]为圆心,半径为1/(1 + g)。
从等式3.5,我们可以推导出下面的式子:
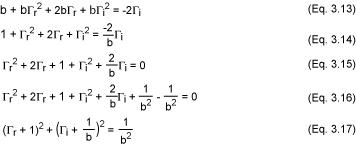
同样得到(x - a)² + (y - b)² = R²型的参数方程(方程3.17)。
求解等效阻抗
当解决同时存在串联和并联元件的混合电路时,可以使用同一个史密斯圆图,在需要进行从z到y或从y到z的转换时将图形旋转。
考虑图8所示网络(其中的元件以Z0 = 50Ω进行了归一化)。串联电抗(x)对电感元件而言为正数,对电容元件而言为负数。而电纳(b)对电容元件而言为正数,对电感元件而言为负数。
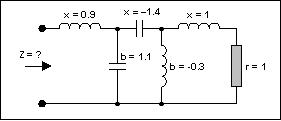
图8. 一个多元件电路
这个电路需要进行简化(见图9)。从最右边开始,有一个电阻和一个电感,数值都是1,我们可以在r = 1的圆周和I=1的圆周的交点处得到一个串联等效点,即点A。下一个元件是并联元件,我们转到导纳圆图(将整个平面旋转180°),此时需要将前面的那个点变成导纳,记为A'。现在我们将平面旋转180°,于是我们在导纳模式下加入并联元件,沿着电导圆逆时针方向(负值)移动距离0.3,得到点B。然后又是一个串联元件。现在我们再回到阻抗圆图。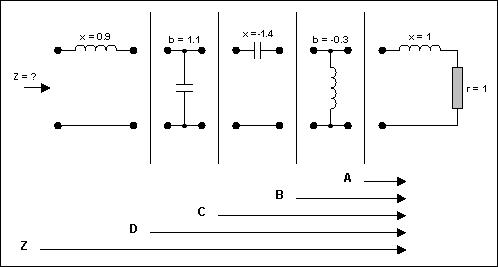
图9. 将图8网络中的元件拆开进行分析
在返回阻抗圆图之前,还必需把刚才的点转换成阻抗(此前是导纳),变换之后得到的点记为B',用上述方法,将圆图旋转180°回到阻抗模式。沿着电阻圆周移动距离1.4得到点C就增加了一个串联元件,注意是逆时针移动(负值)。进行同样的操作可增加下一个元件(进行平面旋转变换到导纳),沿着等电导圆顺时针方向(因为是正值)移动指定的距离(1.1)。这个点记为D。最后,我们回到阻抗模式增加最后一个元件(串联电感)。于是我们得到所需的值,z,位于0.2电阻圆和0.5电抗圆的交点。至此,得出z = 0.2 + j0.5。如果系统的特性阻抗是50Ω,有Z = 10 + j25Ω (见图10)。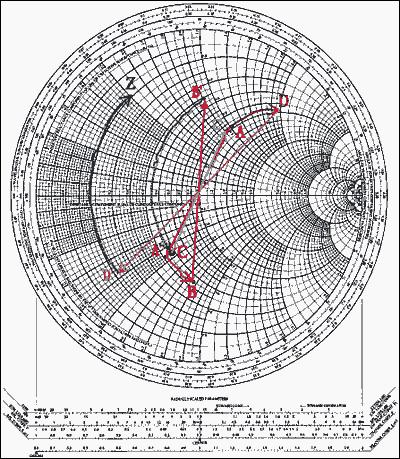
图10. 在史密斯圆图上画出的网络元件
逐步进行阻抗匹配史密斯圆图的另一个用处是进行阻抗匹配。这和找出一个已知网络的等效阻抗是相反的过程。此时,两端(通常是信号源和负载)阻抗是固定的,如图11所示。我们的目标是在两者之间插入一个设计好的网络已达到合适的阻抗匹配。
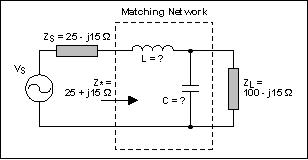
图11. 阻抗已知而元件未知的典型电路
初看起来好像并不比找到等效阻抗复杂。但是问题在于有无限种元件的组合都可以使匹配网络具有类似的效果,而且还需考虑其它因素(比如滤波器的结构类型、品质因数和有限的可选元件)。实现这一目标的方法是在史密斯圆图上不断增加串联和并联元件、直到得到我们想要的阻抗。从图形上看,就是找到一条途径来连接史密斯圆图上的点。同样,说明这种方法的最好办法是给出一个实例。
我们的目标是在60MHz工作频率下匹配源阻抗(ZS)和负载阻抗(zL) (见图11)。网络结构已经确定为低通,L型(也可以把问题看作是如何使负载转变成数值等于ZS的阻抗,即ZS复共轭)。下面是解的过程:
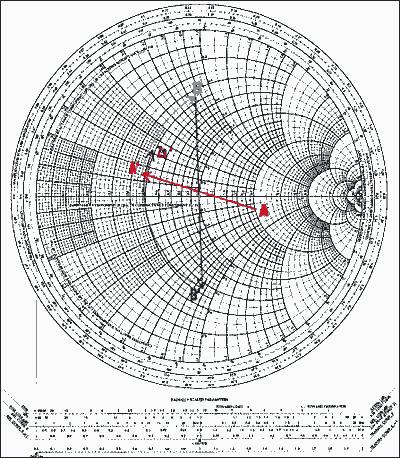
图12. 图11的网络,将其对应的点画在史密斯圆图上
要做的第一件事是将各阻抗值归一化。如果没有给出特性阻抗,选择一个与负载/信号源的数值在同一量级的阻抗值。假设Z0为50Ω。于是zS = 0.5 - j0.3,z*S = 0.5 + j0.3,ZL = 2 - j0.5。下一步,在图上标出这两个点,A代表zL,D代表z*S
然后判别与负载连接的第一个元件(并联电容),先把zL转化为导纳,得到点A'。
确定连接电容C后下一个点出现在圆弧上的位置。由于不知道C的值,所以我们不知道具体的位置,然而我们确实知道移动的方向。并联的电容应该在导纳圆图上沿顺时针方向移动、直到找到对应的数值,得到点B (导纳)。下一个元件是串联元件,所以必需把B转换到阻抗平面上去,得到B'。B'必需和D位于同一个电阻圆上。从图形上看,从A'到D只有一条路径,但是如果要经过中间的B点(也就是B'),就需要经过多次的尝试和检验。在找到点B和B'后,我们就能够测量A'到B和B'到D的弧长,前者就是C的归一化电纳值,后者为L的归一化电抗值。A'到B的弧长为b = 0.78,则B = 0.78 × Y0 = 0.0156S。因为ωC = B,所以C = B/ω = B/(2πf) = 0.0156/[2π(60 × 106)] = 41.4pF。
B到D的弧长为× = 1.2,于是X = 1.2 × Z0 = 60Ω。由ωL = X,得L = X/ω = X/(2πf)= 60/[2π(60 × 106)] = 159nH。
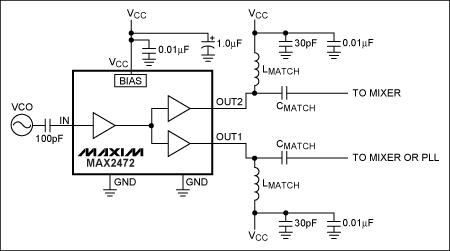
图13. MAX2472典型工作电路
第二个例子是MAX2472的输出匹配电路,匹配于50Ω负载阻抗(zL),工作品率为900MHz (图14所示)。该网络采用与MAX2472数据资料相同的配置结构,上图给出了匹配网络,包括一个并联电感和串联电容,以下给出了匹配网络元件值的查找过程。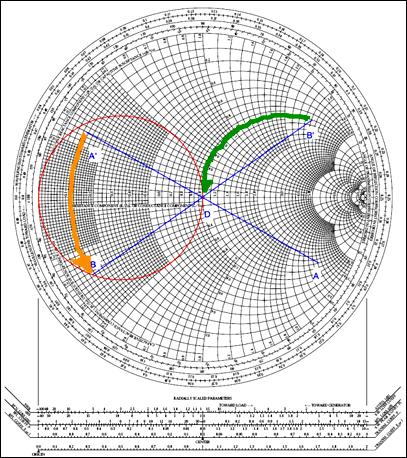
图14. 图13所示网络在史密斯圆a图上的相应工作点
首先将S22散射参数转换成等效的归一化源阻抗。MAX2472的Z0为50Ω,S22 = 0.81/-29.4°转换成zS = 1.4 - j3.2,zL = 1和zL* = 1。下一步,在圆图上定位两个点,zS标记为A,zL*标记为D。因为与信号源连接的是第一个元件是并联电感,将源阻抗转换成导纳,得到点A’。
确定连接电感LMATCH后下一个点所在的圆弧,由于不知道LMATCH的数值,因此不能确定圆弧终止的位置。但是,我们了解连接LMATCH并将其转换成阻抗后,源阻抗应该位于r = 1的圆周上。由此,串联电容后得到的阻抗应该为z = 1 + j0。以原点为中心,在r = 1的圆上旋转180°,反射系数圆和等电纳圆的交点结合A’点可以得到B (导纳)。B点对应的阻抗为B’点。
找到B和B'后,可以测量圆弧A'B以及圆弧B'D的长度,第一个测量值可以得到LMATCH。电纳的归一化值,第二个测量值得到CMATCH电抗的归一化值。圆弧A'B的测量值为b = -0.575,B = -0.575 × Y0 = 0.0115S。因为1/ωL = B,则LMATCH = 1/Bω = 1/(B2πf) = 1/(0.01156 × 2 × π × 900 × 106) = 15.38nH,近似为15nH。圆弧B'D的测量值为× = -2.81,X = -2.81 × Z0 = -140.5Ω。因为-1/ωC = X,则CMATCH = -1/Xω = -1/(X2πf) = -1/(-140.5 × 2 × π × 900 × 106) = 1.259pF,近似为1pF。这些计算值没有考虑寄生电感和寄生电容,所得到的数值接近与数据资料中给出的数值:LMATCH = 12nH和CMATCH = 1pF。
总结
在拥有功能强大的软件和高速、高性能计算机的今天,人们会怀疑在解决电路基本问题的时候是否还需要这样一种基础和初级的方法。
实际上,一个真正的工程师不仅应该拥有理论知识,更应该具有利用各种资源解决问题的能力。在程序中加入几个数字然后得出结果的确是件容易的事情,当问题的解十分复杂、并且不唯一时,让计算机作这样的工作尤其方便。然而,如果能够理解计算机的工作平台所使用的基本理论和原理,知道它们的由来,这样的工程师或设计者就能够成为更加全面和值得信赖的专家,得到的结果也更加可靠。




 /3
/3 
