交流电路中消耗的电能可以用直角三角形的三个边来表示,通常称为功率三角形
我们在关于交流电路的电力教程中看到过其中包含电阻和电容或电阻和电感,或两者都包含有功功率和无功功率。因此,为了让我们计算消耗的总功率,我们需要知道电压和电流的正弦波形之间的相位差。
在交流电路中,电压和电流波形是正弦波,所以他们的振幅随时间不断变化。由于我们知道功率是电压乘以电流(P = V * I),因此当两个电压和电流波形相互对齐时,将发生最大功率。
也就是说,它们的峰值和零交叉点同时出现。当发生这种情况时,两个波形被称为“同相”。
交流电路中的三个主要部件会影响电压和电流波形之间的关系,从而影响它们的相位差,定义电路的总阻抗的是电阻器,电容器和电感器。
交流电路的阻抗(Z)等于直流电路中计算的电阻,阻抗以欧姆为单位。对于AC电路,阻抗通常定义为电路元件产生的电压和电流相量的比率。相量是以这样的方式绘制的直线,即通过其长度和相对于其他相量线的相位差来表示电压或电流幅度,其相对于其他相量的角位置。
AC电路包含将电阻和电抗组合在一起以提供限制电路周围电流的总阻抗(Z)。但是,交流电路阻抗不等于电阻和反应欧姆值的代数和,因为纯电阻和纯电抗相互异相90° o 。但是我们可以使用这个90 o 相位差作为直角三角形的边,称为阻抗三角形,阻抗是由毕达哥拉斯定理确定的斜边。
电阻,电抗和阻抗之间的几何关系可以通过使用如图所示的阻抗三角形直观地表示。
阻抗三角形
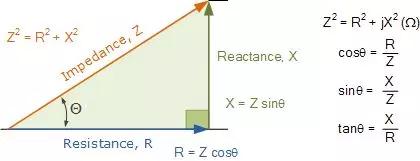
请注意,阻抗是电阻和电抗的矢量和,它不仅具有幅度(Z),而且还具有相角(θ),它代表相位差(θ)。阻力和电抗。还要注意,随着频率的变化,三角形会因电抗的变化而改变形状,(X)。当然,电阻(R)将始终保持不变。
我们可以通过将阻抗三角形转换为代表交流电路中三个功率元件的功率三角形来进一步采用这一思路。欧姆定律告诉我们,在直流电路中,功率(P)(单位为瓦特)等于电流平方(I 2 )乘以电阻(R)。因此,我们可以将上面阻抗三角形的三边乘以I 2,得到相应的幂三角形:
Real PowerP = I 2 RWatts,(W)
Reactive PowerQ = I 2 XVolt-amperes Reactive,( VAr)
表观PowerS = I 2 ZVolt-amperes,(VA)
01交流电路中的实际功率
有功功率(P),也称为真功率或有功功率,在电路中执行“实际工作”。以瓦特为单位测量的实际功率定义了电路的电阻部分所消耗的功率。然后,AC电路中的实际功率(P)与DC电路中的功率P相同。就像直流电路一样,它总是按I 2 * R计算,其中R是电路的总电阻分量。
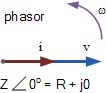
由于电阻不会在电压和电流波形之间产生任何相量差异(相移),所有有用的功率都会直接传递给电阻并转换为热量,光线和工作。那么电阻消耗的功率就是实际功率,这基本上就是电路的平均功率。
为了找到实际功率的相应值,有效值电压和电流值乘以相角的余弦, θ如图所示。
Real PowerP = I 2 R = V * I * cos(θ)瓦特,(W)
但由于它们在电阻电路中的电压和电流之间没有相位差,因此两个波形之间的相移将为零(0)。然后:
交流电路中的实际功率
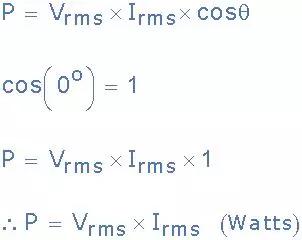
其中实际功率(P)以瓦特为单位,电压( V)是有效值电压,电流(I)是有效值安培。
然后实际功率是以瓦特为单位测量的I 2 * R电阻元件,这是你读到的在您的公用事业能量计上,单位为瓦特(W),千瓦(kW)和兆瓦(兆瓦)。请注意,实际功率P始终为正。
交流电路中的无功功率
无功功率(Q),(有时称为无功功率)是交流电路中消耗的功率不会执行任何有用的工作,但会对电压和电流波形之间的相移产生很大影响。无功功率与电感和电容产生的电抗有关,抵消了有功功率的影响。直流电路中不存在无功功率。

与完成所有工作的有功功率(P)不同,无功功率(Q)需要功率由于感应磁场和电容静电场的产生和减少而远离电路,从而使真正的电源更难直接向电路或负载供电。
在其磁场中的电感器试图控制电流,而由电容器静电场存储的电力试图控制电压。结果是电容器“产生”无功功率并且电感器“消耗”无功功率。这意味着它们都消耗并向源返回功率,因此没有消耗实际功率。
为了找到无功功率,均方根电压和电流值乘以相角的正弦,θ如图所示。
无功功率Q = I 2 X = V * I * sin(θ)伏安无功,(VAr's)
由于纯电抗(电感或电容)中的电压和电流波形之间存在90 o 相位差,所以将V * I乘以sin (θ)给出一个彼此异相90°的垂直分量,因此:
交流电路中的无功功率
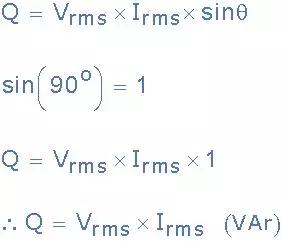
无功功率(Q)为伏安无功,电压(V)为有效值电压,电流(I)为有效值安培。
然后,无功功率代表伏特和安培的乘积,彼此相位相差90°,但通常可以有任何相位角,电压和电流之间的θ。
T.无功功率是I 2 X无功元件,其单位为伏安无功(VAr),千伏安无功(kVAr)和兆瓦安 - 无功(MVAr)。
02交流电路中的视在功率
我们已经看到,实际功率通过电阻消耗,并且无功功率被提供给电抗。因此,由于电阻电阻和电抗元件之间的差异,电流和电压波形不同相。
然后在实际功率(P)与电流之间存在数学关系。无功功率(Q),称为复功率。施加到AC电路的均方根电压V和流入该电路的均方根电流I的乘积称为“伏安产品”(VA),给定符号S,其大小通常称为视在功率。/ p>
这个复数幂不等于加在一起的实数和无功功率的代数和,而是以伏安(VA)给出的P和Q的矢量和。它是由功率三角形表示的复杂功率。伏安产品的均方根值通常被称为视在功率,“显然”这是电路消耗的总功率,即使完成工作的实际功率要少得多。
由于视在功率由两部分组成,即以瓦为单位的同相功率或实际功率的电阻功率和以伏安为单位的异相功率的无功功率,我们可以显示矢量以功率三角形的形式添加这两个功率分量。功率三角形有四个部分:P,Q,S和θ。
在交流电路中构成功率的三个元素可以通过直角三角形的三边以图形方式表示,与前一个阻抗三角形相同。水平(相邻)侧表示电路实际功率(P),垂直(相对)侧表示电路无功功率(Q),斜边表示所示功率三角形的所得视在功率(S)。
交流电路的功率三角
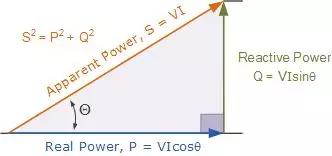
其中:
P是I 2 * R或实际功率,以瓦特为单位执行工作,W
Q是I 2 * X或以伏安无功方式测量的无功功率,VAr
S是I 2 * Z或视在功率以伏安为单位测量,VA
θ是以度为单位的相位角。相角越大,无功功率越大
Cos(θ)= P / S = W / VA =功率因数,pf
Sin(θ)= Q / S = VAr / VA
Tan(θ)= Q / P = VAr / W
功率因数计算为实际功率与视在功率之比因为这个比率等于cos(θ)。
03交流电路中的功率因数
功率因数cos(θ)是交流电路的重要组成部分,也可以用电路阻抗或电路功率的术语。功率因数定义为实际功率(P)与视在功率(S)之比,通常表示为十进制值,例如0.95,或百分比:95%。
功率factor定义了电流和电压波形之间的相位角,I和V是电流和电压的均方根值的大小。注意,相位角是电流相对于电压的差值还是相对于电流的电压无关紧要。数学关系如下:
交流电路的功率因数

我们之前曾说过,在纯电阻电路中,电流和电压波形是彼此同相的,所以消耗的实际功率与视在功率相同,因为相位差为零度(0 o )。因此功率因数将是:
功率因数,pf = cos 0 o = 1.0
<那就是消耗的瓦数与消耗的伏安数相同,产生的功率因数为1.0或100%。在这种情况下,它被称为单位功率因数。
我们上面也说过,在纯粹的电抗电路中,电流和电压波形相互异相90° o 。由于相位差为90度(90 o ),功率因数将为:
功率因数,pf = cos 90 o = 0
即消耗的瓦特数为零,但仍有电压和电流为无功负载供电。显然,降低功率三角形的反应性VAr分量将导致θ减小将功率因数提高到1,单位。还希望具有高功率因数,因为这可以最有效地利用电路向负载提供电流。
然后我们可以写出实际功率,视在功率和电路之间的关系。功率因数为:

电感电路,电流“滞后”据说电压(ELI)具有滞后的功率因数,并且电流“引导”电压(ICE)的电容电路被认为具有超前功率因数。
功率三角示例No1
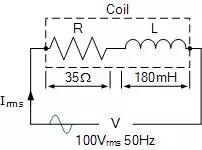
电感为180mH,电阻为35Ω的绕线圈连接到100V 50Hz电源。计算:a)线圈的阻抗,b)电流,c)功率因数,和d)消耗的视在功率。
同时绘制上述线圈的最终功率三角形。
给出的数据:R =35Ω,L = 180mH,V = 100V,ƒ= 50Hz。
(a)线圈的阻抗(Z):
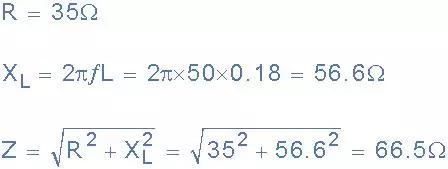
(b)线圈消耗的电流(I):
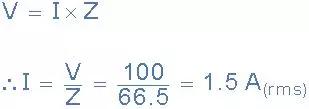
(c)功率因数和相角,θ:
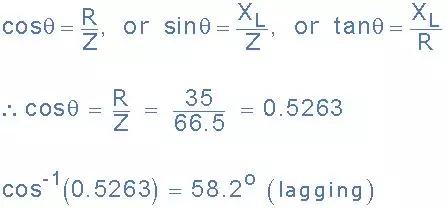
(d)线圈消耗的视在功率(S):

(e)线圈的功率三角形:

作为功率三角形的关系这个简单的例子表明,在功率因数为0.5263或52.63%时,线圈需要150 VA的功率才能产生79瓦的有用功。换句话说,在功率因数为52.63%时,线圈需要大约89%的电流才能完成相同的工作,这会浪费很多电流。
增加一个功率因数校正电容器(对于这个例子a跨越线圈的32.3uF),为了将功率因数增加到超过0.95或95%,将大大降低线圈消耗的无功功率,因为这些电容器充当无功电流发生器,从而减少了消耗的总电流量。
04功率三角和功率因数汇总
我们在这里看到电力的三个要素, Real Power , Reactive Power 和视在功率可以用称为功率三角的三角形的三边来表示。由于这三个元素由“直角三角形”表示,它们的关系可以定义为:S 2 = P 2 + Q 2 ,其中:P 是瓦特(W)的实际功率, Q 是伏安无功(VAr)和 S 是以伏安(VA)为单位的视在功率。
我们还看到,在交流电路中,量cos(θ)称为功率因数。AC电路的功率因数定义为电路消耗的实际功率(W)与同一电路消耗的视在功率(VA)之比。因此,这给了我们:功率因数=实际功率/视在功率,或p.f. = W / VA。
然后,电流和电压之间产生的角度的余弦是功率因数。通常功率因数表示为百分比,例如95%,但也可以表示为十进制值,例如0.95。
当功率因数等于1.0(单位)或100%时,即当实际功耗等于电路视在功率时,电流和电压之间的相角为0 o :cos -1 (1.0)= 0 Ø。当功率因数等于零(0)时,电流和电压之间的相位角将为90 o :cos -1 (0)= 90 Ø。在这种情况下,无论电路电流如何,交流电路消耗的实际功率都为零。
在实际交流电路中,功率因数可以在0到1.0之间,具体取决于连接负载内的无源元件。对于感性电阻负载或电路(最常见的情况),功率因数将“滞后”。在电容 - 电阻电路中,功率因数将是“领先的”。然后可以将交流电路定义为具有单位,滞后或超前功率因数。
功率因数较低且值为零(0)将消耗浪费功率,从而降低电路效率,同时功率因数接近一(1.0)或单位(100%)的电路或负载将更有效。这是因为具有低功率因数的电路或负载需要比相同电路或负载更大的电流,功率因数接近1.0(单位)。
来源:网络







 /5
/5 

