负氧离子具体是什么本文就不介绍了,本文的关键就是介绍负氧离子传感器在研发过程中使用到的关键公式和相关算法,没用的话就不多说了,下面直接开始本文重点内容。
什么是公式?
公式,是指各个量之间的一定关系(如定律或者定理)的式子。
什么是算法?
算法,是对解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。
负氧离子浓度计算公式
在某度或者相关的技术文档中可以找到一条以下公式:
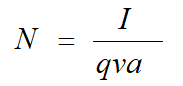
式中,N为每单位体积空气中离子数目(个/cm3),I为微电流计读数(A),q为基本电荷电量(1.6x10-19C),v为取样空气流速(cm/s),a为收集器的有效截面积(cm2)。
公式中已知的量是q(基本电荷量),想要通过这条公式算出N(每单位体积空气中离子数目)还需要获取的量是I电流、v取样空气流速和a收集器的有效截面积。其中v和a与结构相关,按照一定的结构和风扇转速可以获得v和a的值。最后只有I的值需要知道,根据公式说明I为微电流计读数(A),所以整个项目的关键就是准确的获取这个值,看到这里有些厉害的小伙伴可能会觉得获取这个值那不是很简单吗?真的不难吗,下面我跟你解释一下,刚才我也说了获取这个值是整个项目的关键。那是因为获取到的电流的量的单位为fA(飞安)级别。这是一个什么样的级别。跟你科普一下电流的单位,电流的单位有A、mA、uA、nA、pA、fA,单位换算如下:
1A=1000mA;
1mA=1000uA;
1uA=1000nA;
1nA=1000pA;
1pA=1000fA;
I的单位是A,也就是说如果检测到的电流如果是12fA,需要转化为A再带入公式,所以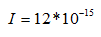
读:12乘以10的负15次方
在这里就出现了一条单位转换公式,假设检测到的电流为x就有;
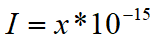
读:x乘以10的负15次方
根据这个就可以知道在电路设计中需要做的事情就是使用现有的硬件放大器芯片去把微弱的电流检测出来。根据相关方案介绍,可以使用一种叫I转V(电流转电压) 的转换放大芯片满足要求。大概的原理图如下:
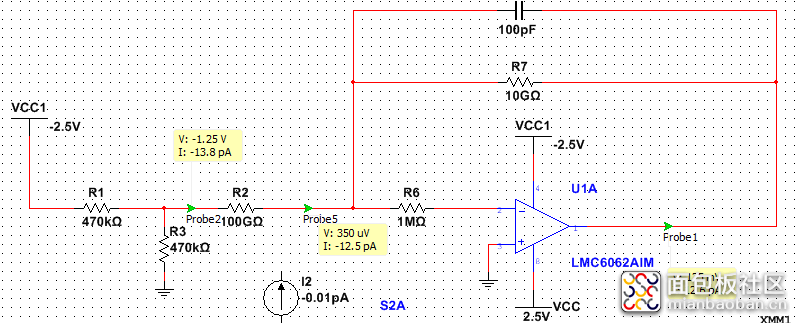
使用电路模拟软件测试电路,通过电阻分压的原理和欧姆定律算出流过电阻的电流(电阻分压和流过电阻的电流都有相关的公式,分压原理公式:I=U/(R1+R2);使用欧姆定律可以算出流过电阻的电流,欧姆定律公式:I=U/R)在本文中由于是使用软件模拟得出结果所以就不再详细说明。分压限流后的输出提供给芯片的输入端,由于输入的是电流值输出的是电压值,所以需要记录数据找出输入输出的关系式。测试不同的输入值所得出的结果存在一定的关系。在这就出现了一条我们之前就已经学过的一条函数公式,一次函数公式:
y=kx+b
式中,把y设定为电路输出的结果值,x设定为电路输入的电流值。通过多组模拟数据带入公式,可以算出公式中k和b的值。然后再验证公式的可行性,就完成的电路的关系式。最终根据电路检测的输出结果值通过验证的公式算出输入端的真实电流值x,所以x=(y-b)/k。
电路所采集到的量到目前为止都是一些模拟量,所以在电路设计中还需要有AD转换(模拟量转换为数据量)的功能模块。根据相关芯片资料描述AD转换芯片存在特定的检测范围。检测的值大于或者小于芯片的检测范围都不能进行正确的转换输出,所以在电路设计中需要加入电压放大电路把小于AD转换芯片的检测范围的模拟量放大到AD转换芯片的检测范围内进行转换, 但是又不能大于AD转换芯片的检测范围所以需要不同的量程去适应。电压放大电路一般都是使用相应的运算放大器把微弱的电压放大。因为通过使用硬件放大电路去把检测值放大了n倍。所以在这个环节量存在着一定的关系,放大后的值不是原本的值,需要通过关系式还原为原本的值。将一个已知的微弱电压提供到放大电路的输入端使用仪器检测电路的输出端的电压很容易就可以知道电路的关系。比如把一个1mV的电压加到输入端,万用表测量输出值显示为10mV,那么之间的倍数就很容易算出,假设电路的倍数为n,输入的已知电压为Vin,经过放大后输出的电压为Vout,即关系式为:
n=Vout/Vin
知道已知放大电路的倍数关系,通过关系式可知真实的输出电压值Vin=Vout/n。不同量程原理一样。
AD转换芯片把模拟量转换为数据量时一般输出的结果值为AD数量值。所以在这也存在着AD值与电压的关系式。相关的换算关系式芯片说明书内都有说到,一般AD值转换为电压的关系式为:
V=adc*Vcal/2~n;(读:adc乘以Vcal除于2的n次方)
式中V为换算结果电压值,adc为芯片转换后的结果值,Vcal为芯片的基准电压,n为ad芯片转换精度(比如有8位、10位、12位、16位、24位)。
AD芯片的转换难免会产生一定的误差,为了提高转换的精度在这需要加入一定的算法去提高转换结果。最简单的方法就是多次转换求平均的方法又叫做"算术平均滤波法"。公式为:
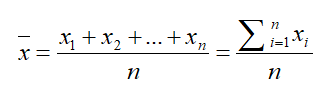
程序设计如下:
#define amf_N 12 //算术平均滤波法采样个数//算术平均滤波 uint16_t Arithmeticmeanfiltering(void) { uint16_t sum; unsigned char count; for ( count=0;count<amf_N;count++) { sum+=Read_ADS(); delay_ms(10); printf("ADC:%d\r\n",Read_ADS()); } return (sum/amf_N); }
复制代码所以在这里另一种算法更适合,叫做"中位值算术平均滤波法"。其实这种算法是算术平均滤波法的一个改良。主要的区别在于对采集的多次数据进行了从小到大的排序,排序的方法为冒泡排序法。排序后去掉最小值和最大值后再求和求平均。中位值算术平均滤波法程序设计过程如下:
uint32_t MedArithmeticmeanfiltering(void){ uint32_t value_buf[amf_N]; unsigned char count,j,i; uint32_t temp=0,sum=0,isSorted; for( count=0;count<amf_N;count++) { value_buf[count]=Read_ADS(); delay_ms(50); } for(j=0;j<amf_N-1;j++) { isSorted=1; for(i=0;i<amf_N-1-j;i++) { if(value_buf[i]>value_buf[i+1]) { temp =value_buf[i]; value_buf[i]=value_buf[i+1]; value_buf[i+1]=temp; isSorted=0; } } if(isSorted)break; } for(count=1;count<amf_N-1;count++ { sum+=value_buf[count]; } return sum/(amf_N-2);
复制代码void bubble_sort(unsigned int *q,int n){ int i,j; for(i = 0;i<n;i++) { for(j = i;j < n;j++) { if(*(q+i)>*(q+j)) { int temp; temp = *(q+i); *(q+i) = *(q+j); *(q+j) = temp; } } }
复制代码写这篇文章也算是对之前的一个项目的公式使用方面的一个总结,通过这个项目使我真正的体验到了基于理论的研发过程。
来源:嵌入式小萧






 /5
/5 



程序上用的算法是冒泡排序法