在有等长要求的场景中,我们通常需要对走线的延迟进行仿真,以确定走线等长约束。实际仿真时,我们可以通过2D电磁场算法计算微带线或者带状线的延迟,也可以提取微带线或者带状线的S参数,然后利用时域仿真器对走线延迟进行分析。
在使用走线S参数对延迟进行时域仿真时,就会牵扯到时域-频域转换问题,可能会出现因S参数抽取不合理导致的仿真错误。本文将提取实际PCB上一段带状线的S参数,对比当S参数频率范围以及点数不同时,时域延迟的差别。
1:仿真参数设置
(1):S参数频率范围为10M~40GHz,点数分别为:401,201,101,91,81, 71,61,51,41;
(2):仿真点数设置为101点,最大频率设置为:4,5,6,7,8,9,10,20,40GHz
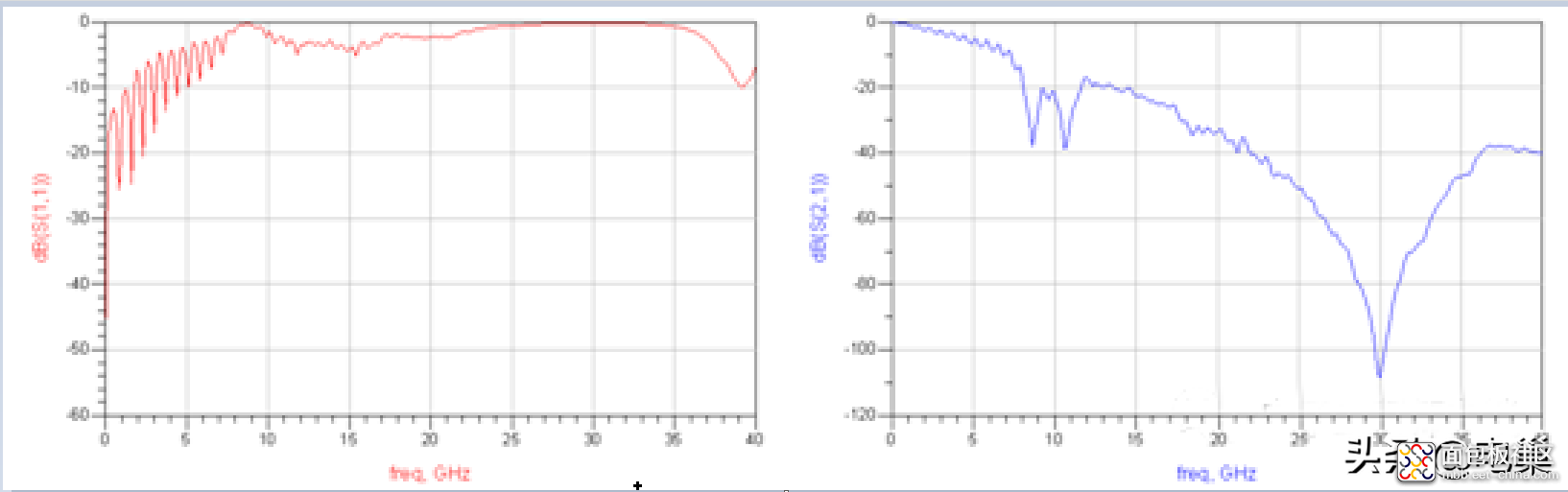
S 参数
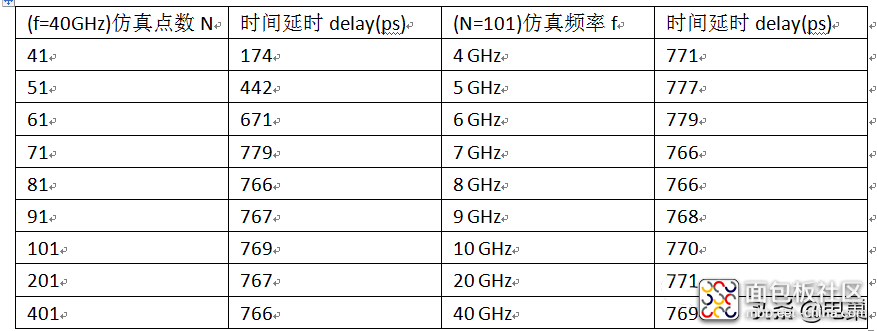
仿真结果如下表所示,可以看到当f=40GHz,点数N<71点时,时间延时delay误差快速增大;当N>81时,delay的值波动小于5ps。N一定,频率f从4GHz变化到40GHz,delay的值波动小于13ps。
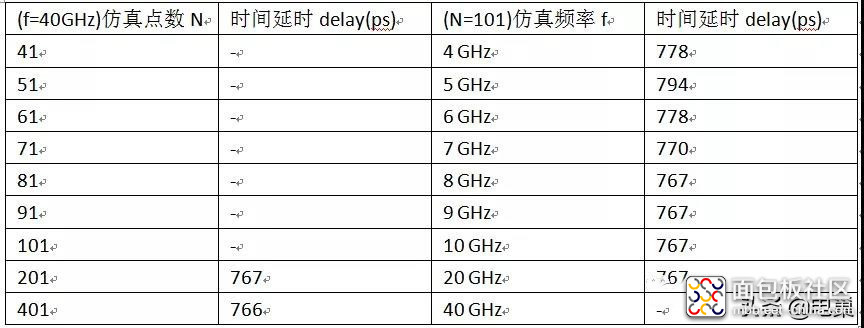
随后使用另一款软件对上面结构进行建模,然后进行时域仿真,仿真结果如下,发现此软件不具有自动差值能力,其先将S参数转换为Spice电路,然后进行时域仿真,N<=101点时,仿真会出错。
3. 结论
对比两款软件的仿真结果基本一致,说明在S参数合适的情况下,使用S参数去计算延迟是可行的。但是当S参数不合理时,使用S参数去评估走线延迟会出现很大的误差,大家在仿真的时候一定要小心。
时域仿真器在时域仿真时如何处理S参数才是理解上面问题的关键,可惜我们不太了解时域仿真器处理的过程,我尝试直接通过FFT计算,发现也与上述仿真结果不能匹配。
在使用走线S参数对延迟进行时域仿真时,就会牵扯到时域-频域转换问题,可能会出现因S参数抽取不合理导致的仿真错误。本文将提取实际PCB上一段带状线的S参数,对比当S参数频率范围以及点数不同时,时域延迟的差别。
1:仿真参数设置
(1):S参数频率范围为10M~40GHz,点数分别为:401,201,101,91,81, 71,61,51,41;
(2):仿真点数设置为101点,最大频率设置为:4,5,6,7,8,9,10,20,40GHz
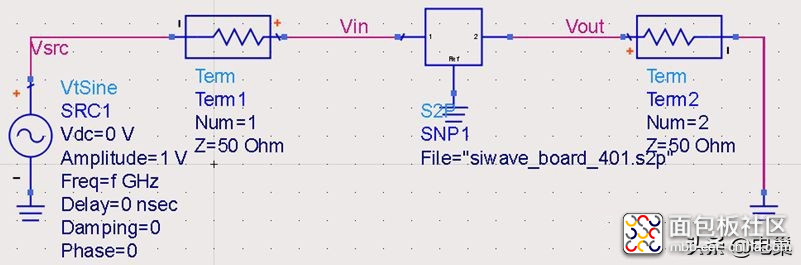
(3):用于时域仿真的激励源为幅度为1V、频率为1GHz的正弦波,频域S参数和时域仿真原理图如下所示:

S 参数

时域仿真原理图
2: 仿真结果仿真结果如下表所示,可以看到当f=40GHz,点数N<71点时,时间延时delay误差快速增大;当N>81时,delay的值波动小于5ps。N一定,频率f从4GHz变化到40GHz,delay的值波动小于13ps。

随后使用另一款软件对上面结构进行建模,然后进行时域仿真,仿真结果如下,发现此软件不具有自动差值能力,其先将S参数转换为Spice电路,然后进行时域仿真,N<=101点时,仿真会出错。

3. 结论
对比两款软件的仿真结果基本一致,说明在S参数合适的情况下,使用S参数去计算延迟是可行的。但是当S参数不合理时,使用S参数去评估走线延迟会出现很大的误差,大家在仿真的时候一定要小心。
时域仿真器在时域仿真时如何处理S参数才是理解上面问题的关键,可惜我们不太了解时域仿真器处理的过程,我尝试直接通过FFT计算,发现也与上述仿真结果不能匹配。







 /5
/5 


