与数学中的微分运算类似,微分电路的作用是对输入信号进行一阶求导,输出信号的大小与输入信号的变化率有关,反映的是信号中的突变部分。可以把矩形脉冲变换为尖脉冲输出,常作为电路的触发信号(LM331的频率-电压转换就利用到了该原理)。
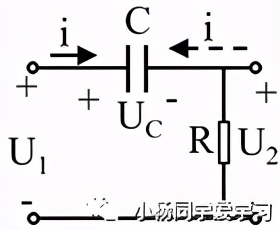
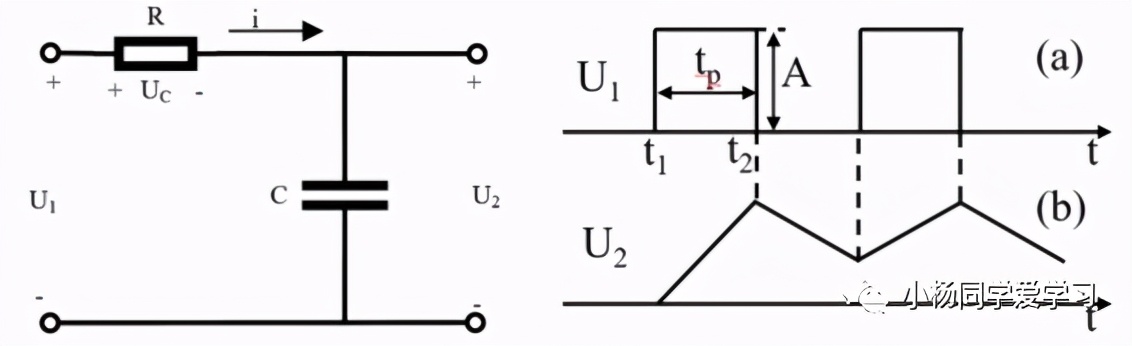
如图1所示,为基本的RC微分电路。初始时,U1=UC=U2=0V。当t=t1时,输入如图2(a)所示的矩形脉冲,由于电容C两端的电压不能突变,所以输入电压的一瞬间UC仍然等于0 (在这一瞬间可以把U1看成交流电,而电容具有通交流、阻直流的作用,所以UC=0V)。由U1=UC +U2,可知此时U2=U1,接着UC两端的电压会呈指数增长,所以,U2两端电压会呈指数下降。
当t=t2时,U1=0V(此时电容C已经充满电),UC=A,电容会通过电阻R放电(电流方向为虚线),U2=-UC,并呈指数减小。电压的变化如图2(b)和(c)所示。
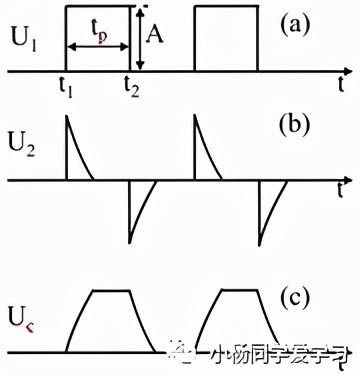
当图1中的电阻R=20kΩ,电容C=100pF时,输入信号的幅值为5V,脉宽为50μs,UC和U2的电压变化如图3所示。
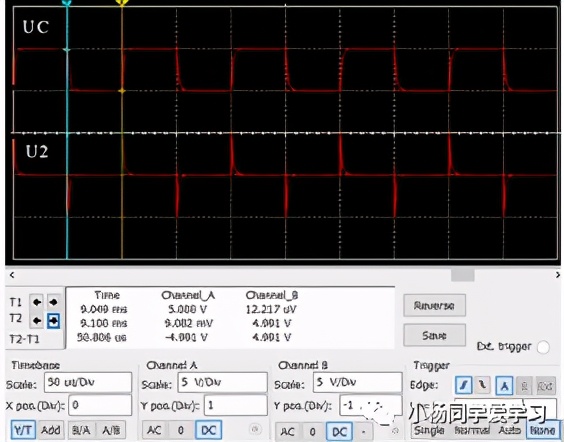
图3 微分电路仿真结果
需要注意的是微分电路中的时间常数τ(RC的乘积)需要远远小于输入信号的脉宽tp(一般τ<0.2tp)。τ越小,电容的充放电速度越快,输出脉冲就越尖,反之则越宽。
当图1中的电阻R=20kΩ,电容C=2.5 nF时,仍输入上述的脉冲信号,此时有τ=tp,UC和U2的电压变化如图4所示,此时U2的输出已经不再是尖脉冲了,也就失去了波形变换的意义了。
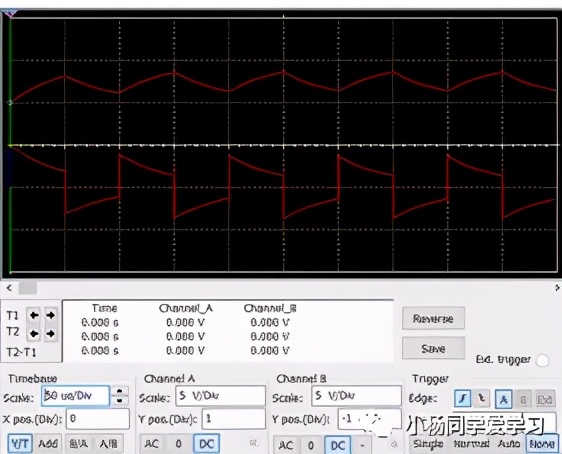
注1:上面的电路也常作为高通滤波器使用,关于滤波器的内容会在后面详细介绍。
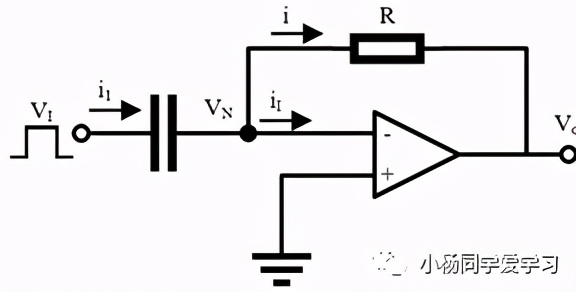
注2:上述电路的输出信号呈指数变化,线性度较差。为了提高电路的线性度和带载能力,常用运算放大器和R、C组成微分电路,其基本形式如图5所示。
由虚短和虚断可知,此时有VN=0,iI=0,所以
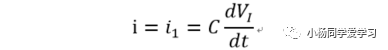
由VN-VO=iR,可知
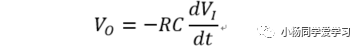
输出电压Vo正比于输入电压对时间的微分,负号表示相位相反。
当输入的是正弦信号VI=sinωt时,输出信号Vo=-RCωcosωt,表明输出信号的幅值与输入信号的频率成正比。由于一般信号都会含有高频谐波,输出信号很有可能被噪声完全淹没,而且该电路容易出现自激振荡,稳定性很差。所以该电路的实用价值不是很高,常用的是如图6所示的改进微分电路。
当R1=R2=R,C1=C2=C,只有输入信号满足f<<fH=1/2πRC时,才具有微分功能,具体推导过程比较复杂,在这里暂不展开。
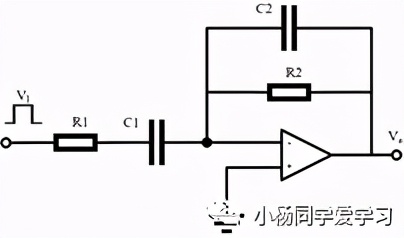
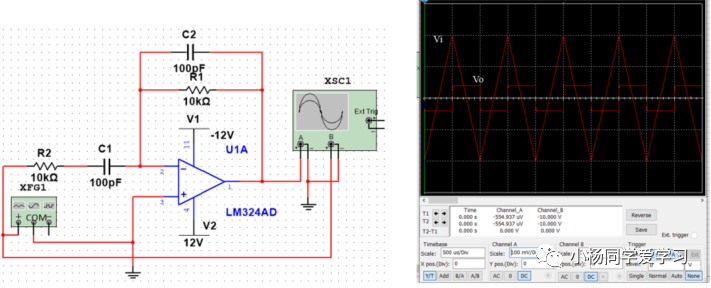
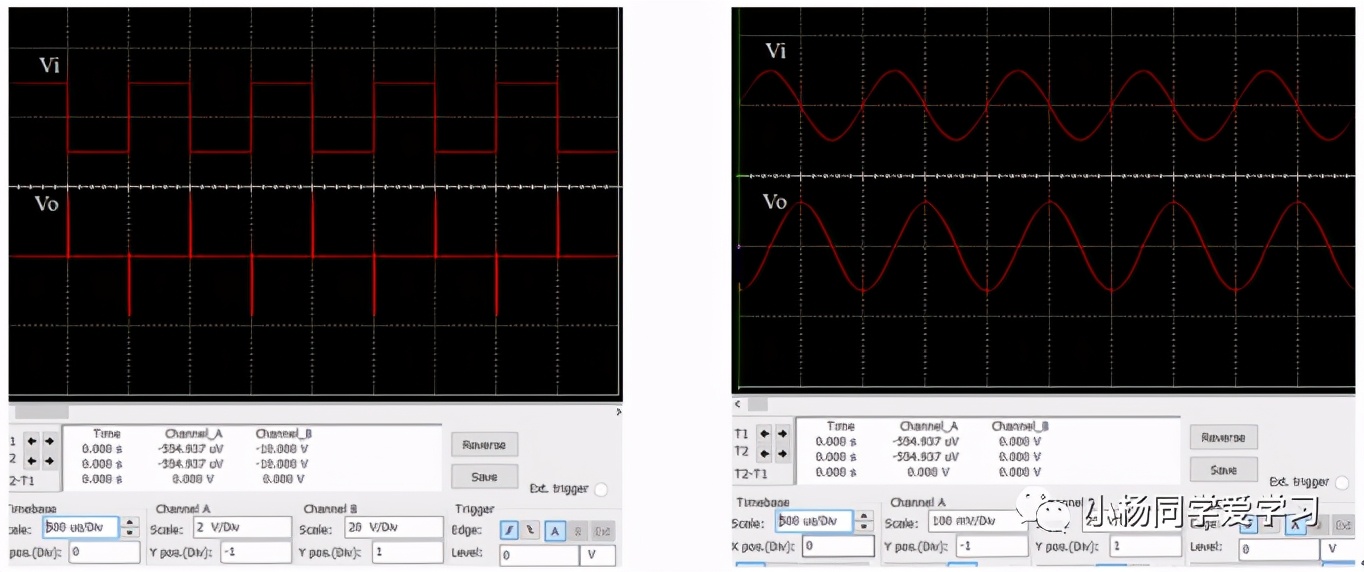
利用Multisim搭建如图7(a)所示的仿真电路,当分别输入1kHz的三角波、矩形波和正弦波时,输出波形如图7(b~d)所示。
将微分电路中的电阻和电容替换一下位置,就得到了如图8(a)所示的积分电路。这个电路比较容易理解,就是利用电容两端电压不能突变的原理,当U1=A时,给电容C充电,U2逐渐增加;当U1=0时,电容C通过电阻R放电,U2逐渐降低,循环往复。积分电路可以用来将矩形波变成锯齿波输出,成立的条件是时间常数RC>>tp,否则电压C将会出现电压饱和。
注3:上述电路也常作为低通滤波器使用,关于滤波器的内容会在后期详细介绍。
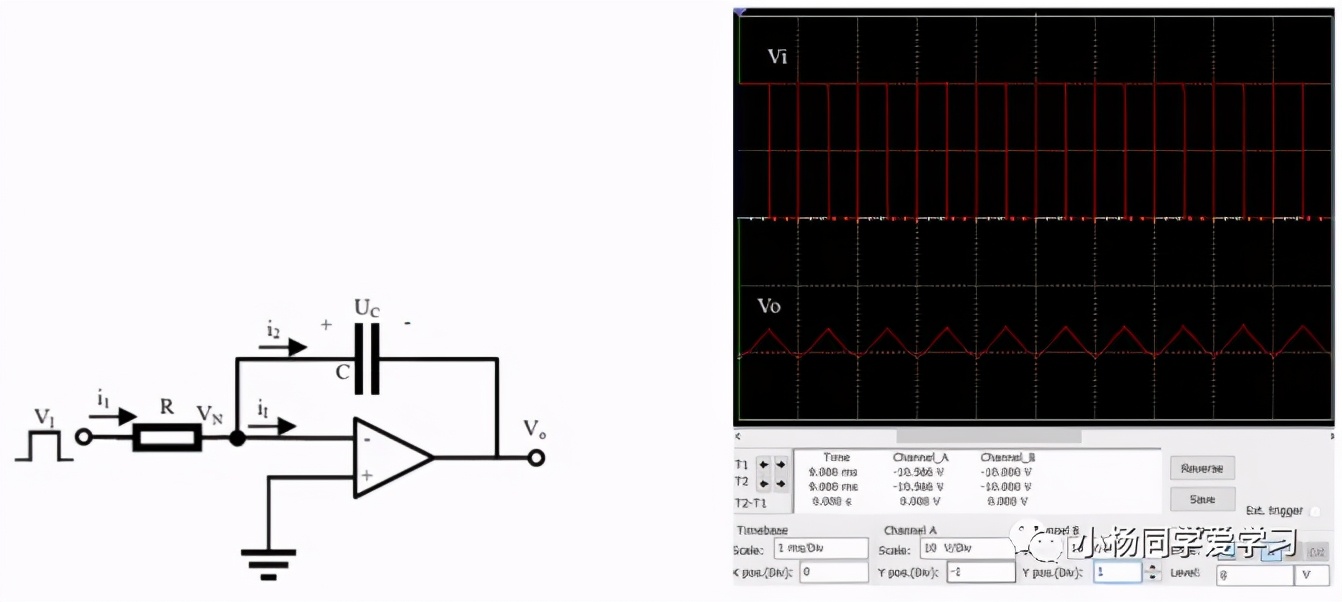
注4:由于上述电路中,电容C两端的电压是呈指数变化的,所以输出电压U2与输入电压U1的线性关系较差。为了提高输出电压与输入电压的线性度,可以采用运算放大器和R、C组成积分电路,如图9(a)所示。
同样由虚短和虚断可知,VN=0,iI=0,故有
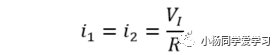
由电容的电压变化关系可知
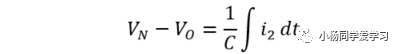
所以
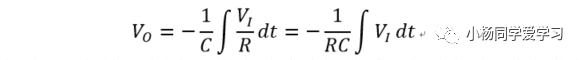
输出电压Vo与输入电压VI的积分成线性关系,负号表示二者相位相反。利用Multisim得到的仿真结果如图9(b)所示。
如图10(a)所示,当开关S1(通常为MOS管)闭合时,电源Ui对电容C充电,UC增加,充电结束后,Uo=UC=Ui,这个过程通常称为采样阶段。当S1断开后,由于电容C没有放电回路,所以UC会保持不变,直到开关S1再次闭合,这个过程通常称为保持阶段,输入信号与输出信号的变化如图12(b)所示。其中运算放大器A通常选用具有高输入阻抗,和低输出阻抗的器件,以尽量减少电容C上的电荷泄漏,并提高电路的带负载能力,这个电路在AD采集等场合应用较为广泛。
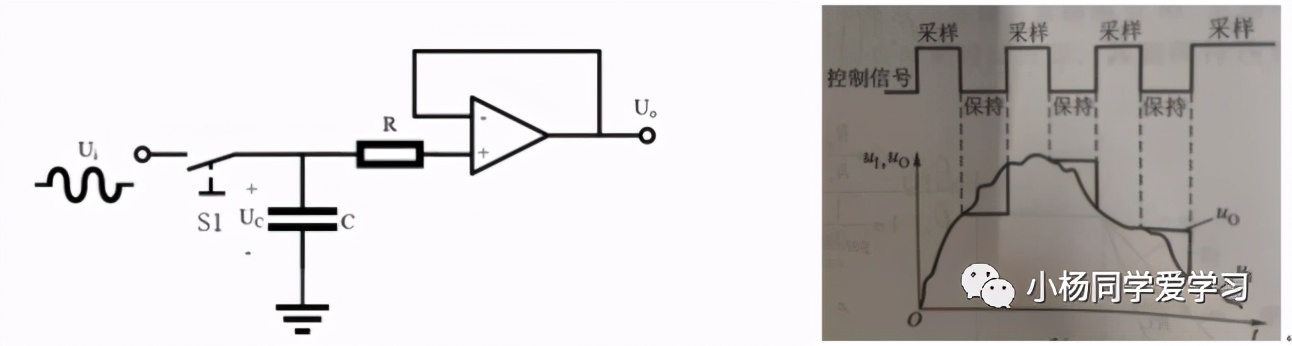
图10 (a)采样电路 (b)输入与输出波形
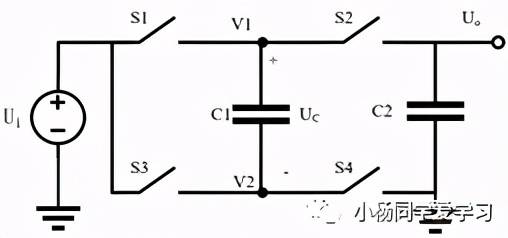
现实中“泵”的主要作用就是增大液体或者气体的压力,然后对外输出。顾名思义,电荷泵的主要作用就是利用电荷来增大电路的压力,也就是在输出端产生比输入端更大的电压,在这里电容器主要起到了储存电荷(储能)的作用。基本原理如图11所示,其中的开关S1~S4通常为MOS管(NMOS或者PMOS),工作过程主要分为两个阶段:
充电阶段:S1和S4闭合,S2和S3打开,电源Ui给电容C1充电,充满后有UC=V1-V2=Ui。
转移阶段:S2和S3闭合,S1和S4打开,V2=Ui,由于电容两端电压不能突变,因此V1=V2+UC=2Ui,实现了电压的倍压。
除此之外,还有负压、1.5倍压、三倍压和倍压等不同的电荷泵电路,但是基本原理都是一样的,就是利用了电容两端电压不能突变的性质。







 /5
/5 


