本章将对空间几何的一些基本概念进行解释,并将其与线性代数中的基本概念进行简单映射,这种映射对于今后的学习是有益的。之后对矩阵概念和算法进行详细阐述,帮助对线性代数不甚了解的读者进行学习。如果读者已经熟悉线性代数的相关概念,那么可以略过本章或仅了解一些几何概念。
本章会略去一些对数学证明很重要但在机器学习中很少用到的概念。很多深度学习内容实际上并无完善的理论约束,这也是很多研究人员努力的方向。如果希望从事相关研究工作,则需要进行更加深入、完整的学习。
1.1多维几何空间本节将对空间几何中的相关概念进行阐述。这种阐述是基于"直觉"的,也就是帮助读者建立空间与函数的知识体系并将其与机器学习联系起来。这并不是严格的数学证明过程。对于学习而言,这种“直觉"是必要的。让理论符合我们的"直觉",是更进一步学习的基础
1.1.1空间、函数和向量
首先介绍的概念是空间函数,在此之前我们需要了解什么是空间笛卡儿坐标。这里将空间的每一个点(使用P、Q等表示)进行编号,用一组实数x1,x2,. ..,xn与之相对应,此时称这组实数为坐标。当且仅当两个坐标值相等时代表的才是同一个点。也就是说,当空间点与坐标为-对应的关系时,这种坐标称为笛卡儿坐标,记为R^n ,n称为此空间的维数。对于读者来讲,比较容易理解的是二维、三维空间,如图1.1所示。
图1.1 空间以及其中的坐标点
在空间区域,可以定义一个函数f(p)=f(x1,...,xn),这构成了n维空间中的函数。如果空间坐标满足:连接空间中任意两点P、Q,直线的长度平方公式如下。
(1.1)
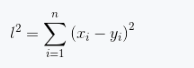
如式(1.1)所示,称这种坐标系为欧式空间。欧式空间是一种简单的空间形式,从零点开始指向空间中某一点的坐标称为坐标向量,如图1.2所示。坐标向量在欧式空间中是可以直接相加的。
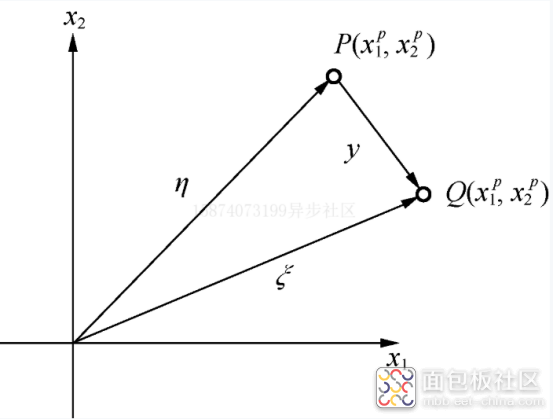
图1.2 二维欧式空间中的坐标向量
欧式空间中的坐标向量是可以直接进行代数运算的。例如,图1.2中展示的坐标向量的关系如下。
(1.2)
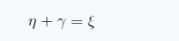
在此二维空间所有的坐标向量中,有两个特殊的向量: e1 =(0,1), e2= (1,0),其长度均为1,并且互相正交。此二维空间中所有的坐标向量都可以由这两个向量通过某种代数运算得到,因此这两个向量称为坐标基向量,向量
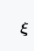
可表示为式(1.3)
(1.3)
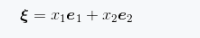
如果已知n维空间中的向量
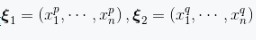
,那么
(1.4)
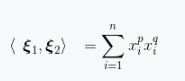
称为欧几里得内积,在机器学习中也称为向量乘积。如果两个向量内积为0,则称两个向量正交。假设在空间中定义了关于坐标的某种函数约束
(1.5)
f(x1,...,xn)=0,...,fk(x1,...,xn)=0
由于多维空间情况不太好理解,因此以三维空间中的一维曲线为例进行说明。三维空间中一维曲线需要使用两个方程约束,也就是只有一个自由度,这个自由度可以用变量t表示。此时三维空间中的一维曲线的另外一种表示形式为式(1.7)。(1.7)
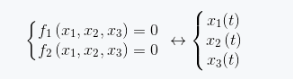
将式(1.7)所表示的关系绘制为空间中的曲线,如图1.3所示。
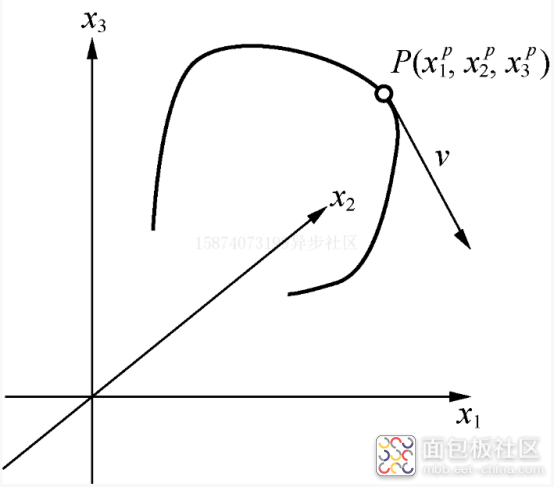
图1.3 三维空间中的曲线和速度向量
图1.3展示了式(1.7)所描述的三维空间中的一维曲线。这里有了向量的另外一种定义一速度,其形式如式(1.8)。
(1.8)
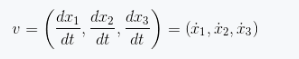
速度表示了空间曲线的变化情况。
注意:这里的速度也是一个向量,但是与前面提到的坐标向量不同。速度代表了空间曲面的特征,而坐标向量是带有位置信息的,之后我们所讨论的坐标变换也是对于位置向量而言的。在机器学习问题中,我们通常不太纠结于两种向量的区别,因为它们均是在欧氏空间之中。
式(1.7)描述了空间曲线。空间几何体在空间中都具有一定的连续性,这种空间上的连续性使我们可以从曲线拟合的角度看待机器学习问题。对于一般的机器学习问题而言,空间曲线的数学形式是未知的。这就需要通过数据点去预测曲线形状,这些数据点是对未知曲线的采样,也就是从曲线上选择的一些数据点。很多时候这些数据点是带噪声的。恢复未知曲线最简单的方式是插值法。这里插值指的是通过已知空间曲线的若干点取值来预测其他数据点位置。
图1.4是插值法示意图,我们只知道空间中的点P、Q、R.如果需要计算在空间中某一点x1处所对应的x2取值,则从函数角度来说,就是获取空间曲面的近似值。
(1.9)

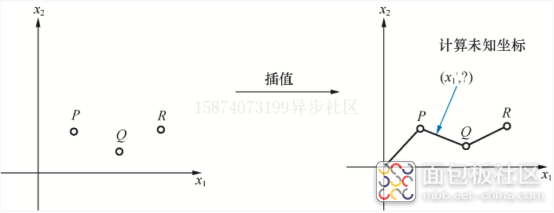
图1.4插值法示意图
这是一种朴素的机器学习过程,整个过程我们只是用直线来连接空间中的数据点。为解释这个问题,我们列举一个更常见的多维空间的问题,对于手写数字而言,其是一个28x28大小的灰度图。从空间几何角度来说,是一个28x28=784维空间,每个像素点为一个坐标,不同值代表不同灰阶, 0~1代表从黑到白。将整个图像沿竖直方向移动,移动量为h,此时可以将每个像素点都看成是移动量/的函数。由此构建了一个在784维空间中的一维曲面,这个高维空间中的曲面是难以观测的,因此使用主成分分析方法(PCA方法)对高维空间进行降维,从而将其可视化,如图1.5所示。
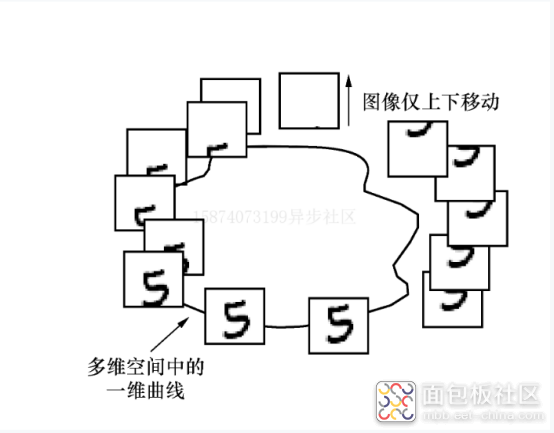
图1.5 784维空间一维曲线
图1.5展示了多维空间中的一维曲线,这是PCA方法降维之后可视化的结果。可以看到,图像在竖直方向产生微小改变后,多维曲线依然具有一定的连续性。这使我们可以不必精确地用函数来描述变化过程,而只需要使用几个点就可以大概地描述整个图像移动的过程。机器学习问题本身的泛化性能也来源于此。后面会对PCA方法进行讲解。
1.1.2 空间变换与矩阵
如果在空间中包含两种坐标系,而坐标之间符合函数关系,则这种函数关系称为空间变换。
(1.10)
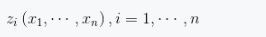
简单的空间变换形式为空间的旋转、平移和拉伸。这种变换称为仿射变换,如图1.6所示。
(1.11)
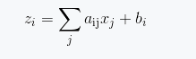
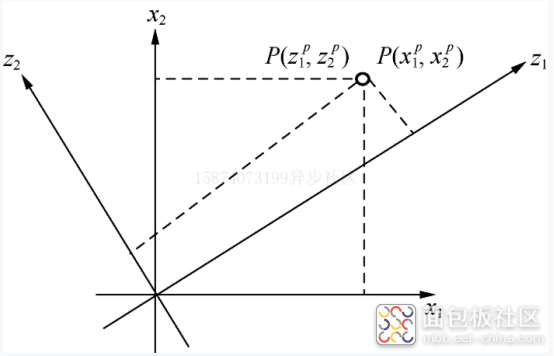
图1.6 二维空间的仿射变换(旋转)
为了书写方便,这里将式(1.11)表示的代数计算写成矩阵形式。
(1.12)
Z=Ax+b
这里A是二维矩阵。矩阵是深度学习中的基本概念,深度学习的建模以及优化过程都是围绕矩阵进行的。在这里矩阵指的是将一系列的代数运算按照某种方式组织起来。矩阵概念映射到计算机科学中就是数组。(1.13)
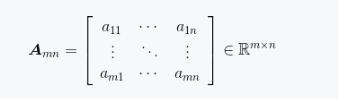
在式(1.13)中, R^m*n代表m行n列的实数矩阵。矩阵的表示方式有A或者[aij],对于我们所接触的机器学习问题而言,矩阵内的数值通常为实数。为了说明问题,我们列举一个比较简单的例子,如图1.7所示。
从图1.7可以看到,仿射变换本身包含了图像的旋转与拉伸,但是仿射变换在原始坐标中的直线在变换坐标中依然是直线。仿射变换是一种线性变换。仿射变换可以用于对图像进行简单处理,如图像的拉伸、平移和旋转等,如图1.8所示。
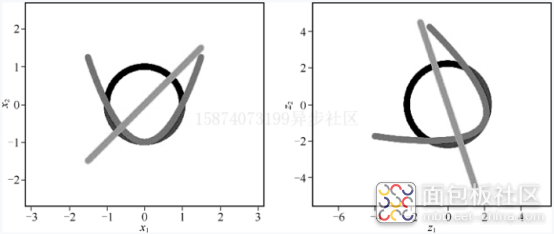
图1.7 二维空间的仿射变换
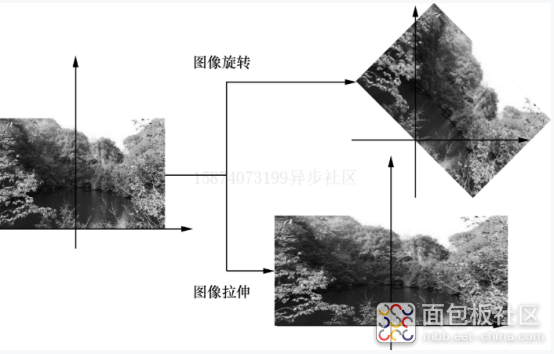
图1.8 对图像进行仿射变换
对于欧式空间中的某一坐标向量,在x、z坐标系中坐标分别为(x1,...,xn)(z1,...,zn),其可以写为基向量相加的形式。
(1.14)
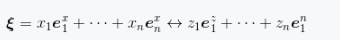
因此,向量在坐标变换中有相似的形式。
(1.15)
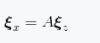
如果存在一个特征向量在线性变换过程中仅是长度方向发生变化,且符合形式
(1.16)
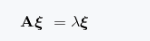
则称

为特征向量,入为特征值。
张量与矩阵的区别
张量本身的定义是在空间中使空间中的某种度量(如长度)不变而成产生的量,因此其产生与几何相关。而矩阵本身则仅代表一种代数运算的组合形式。两者的联系点在于函数和几何空间的映射。
这里列举几种常见的张量(向量)。
速度向量:
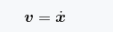
梯度向量:
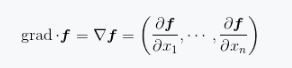
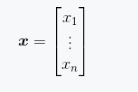
在仿射变换中定义的A就是矩阵,它是独立于空间张量存在的。一维矩阵就是一个机器学习中常说的向量。
列向量:
行向量:
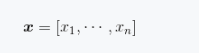
本文节选自《深度学习算法与实践》
来源:异步社区









 /5
/5 


