电感是一种可以将电能转换为电磁能而储存起来的元件,常见的电感主要有:用于EMC抑制的共模电感;用于电流限制(或者说是能量储存)的差模电感;用于能量传输的变压器;用于高频滤波的磁珠等等。电容是一种可以将电能转换为电场能而储存起来的元件,常见的电容主要有:电解电容、安规电容(X电容和Y电容)、薄膜电容、陶瓷电容等等。
说到电感,不得不讲述一下电磁场的相关历史。在一个课堂实验中,某位电磁学先驱偶然发现,通电的导线对旁边不远处的指南针所指的方向有所影响——当导线通电时,指南针与导线平行;当导线断电时,指南针恢复到正常的位置。另一位先驱在此基础上发现,两根距离较近的导线,如果通入同向的电流,则两根导线相互排斥;如果通入异向电流,则两根导线相互吸引。在此基础上提出了洛伦兹力,即现在读者熟知的左手定则(用来判断磁场对电荷的力的作用,集肤效应的缘由;另外右手定则是用来确定电流和磁场的方向)。另另一位先驱在此基础上,将导线绕成环形线圈(即现在读者熟知的螺线管),线圈两端接上电压表,用永磁铁在线圈中插入、取出。这位先驱发现只有在永磁铁与线圈做相对运动时,电压表的指针才会偏移,而且相对运动的速度越快,电压表偏移的角度越大。在此基础上提出了法拉第定律,但是只说明了感应电动势与磁通变化率的关系,但是未能够说明感应电势的方向。另另另另一位先驱,在法拉第定律的基础上,阐明了变化磁通与感应电势产生的感生电流之间在方向上的关系——在电磁感应过程中,感生电流所产生的磁通总是阻碍磁通的变化。即当磁通增加时,感生电流所产生的磁通与原来的磁通方向相反,削弱原磁通的增长;当磁通减小时,感生电流产生的磁通与原来的磁通方向相同,阻止原磁通减小,感生电流总是试图维持原磁通不变。(这些先驱是谁是真的有点记不清,先驱们都是大哥,不会介意这些细节的。。。)
法拉第定律和楞次定律总称为电磁感应定律。假设线圈匝数为N,L为线圈的电感值,电磁感应定律的数学表达式如下:
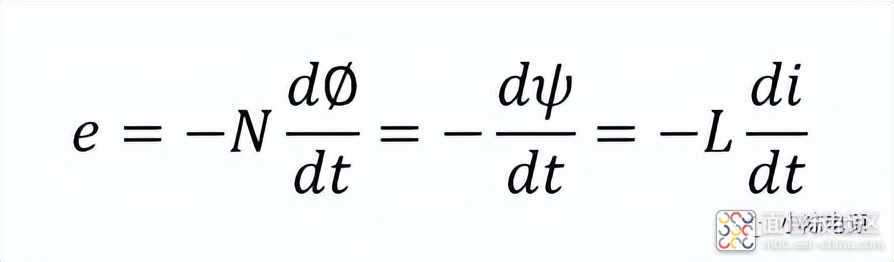
式中:
Φ表示单匝线圈中的磁通;
Ψ表示N匝线圈的磁链,即N匝线圈的磁通总和;
结合电容和电感的对偶电路(图一所示),详细地解释一下电感电流突变时高压是怎么产生的,同时也加深对电磁感应定律的理解。
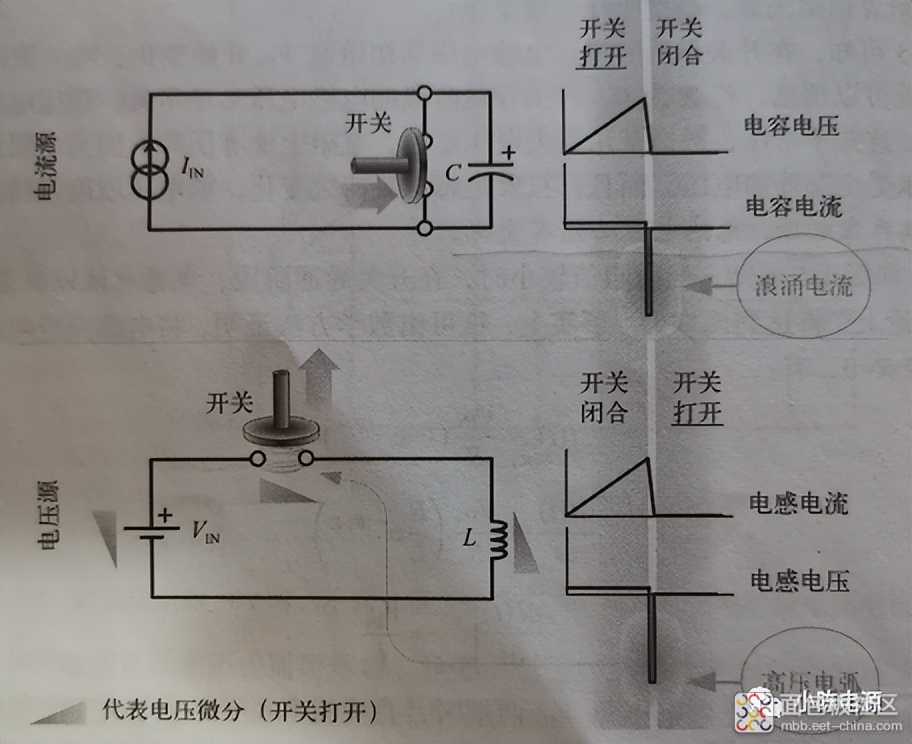
图一 电容和电感的对偶电路
假设电感为理想电感,永远不会饱和,磁芯磁导率不受电感电流增加的影响永远恒定。在开关闭合前,电感电流为零,电感电流的变化率也为零。在开关闭合的瞬间,根据楞次定律,电感将产生感应电动势,阻碍电感电流变化,根据基尔霍夫电压定律,电感电压为Vin,电感电流为零。随着时间的推移,电感电流线性增加。现在突然将开关打开,由于回路的突然断开,回路电流突然降为0。在回路电流为0时,线圈中所储存的能量也为0。也就是说在开关打开的过程中,电感需要将储能的能量完全释放出去。在实验中发现,在开关打开的过程中,开关会出现拉弧的现象,表明电感中储存的能量通过拉弧的形式得到了释放。为啥会拉弧呢?因为开关中触点间的空气被高压击穿了。所以可以得到如下结论——在开关打开瞬间,电感电流发生突变,在开关触点两端产生了能够击穿空气的高压。在常见的电力电子工程应用中(利用电感电流突变进行高压放电的应用除外,比如电棍),一定要杜绝电感电流发生突变的情况,不然很容易击穿回路中的开关元器件。同理,电容两极是不能够短路的,否则电容正负极上的电荷会在瞬间融合,使短路回路中出现瞬间大电流,回路中的元器件可能因为过热而烧毁。
如图一所示的电感和电容的对偶电路,不知有没有读者能够理解为什么电容电路中对应的是电流源而电感电路中对应的是电压源。结合电磁感应定律,上文详细说明了由于电感电流的突变而带来的较大的感生电动势,那么电容与电感对应的对偶电路,就应该是电容电压的突变带来的较大的浪涌电流——电感电流受迫降为零对偶于电容电压受迫降为零。
电感电流不能突变,那实际应用过程中又是怎么回事呢?不知道读者注意到电磁感应定律的数学表达式中的更深层次的含义没有,为了更够更清楚地说明电感电流突变的问题,我们把电磁感应定律的数学表达式copy下来,更方便查看:
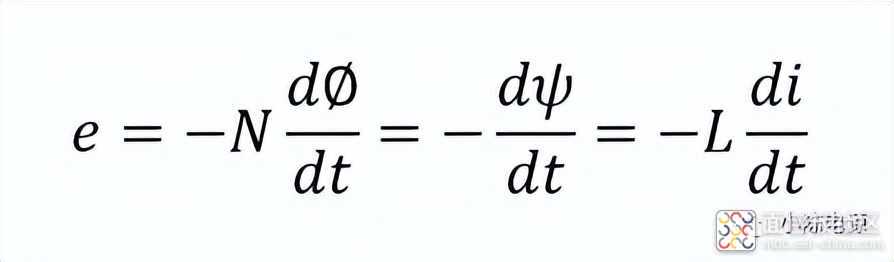
假设L为理想电感,那么L两端的电压e与电流变化率成正比,电流变化率越大,e就越大,假设电流不进行突变,只是电流变化率进行突变呢?从一条具有正上升斜率(储能增加)的曲线跳变到另一条具有下降斜率(符号相反,即储能减少)的曲线,如图二所示:
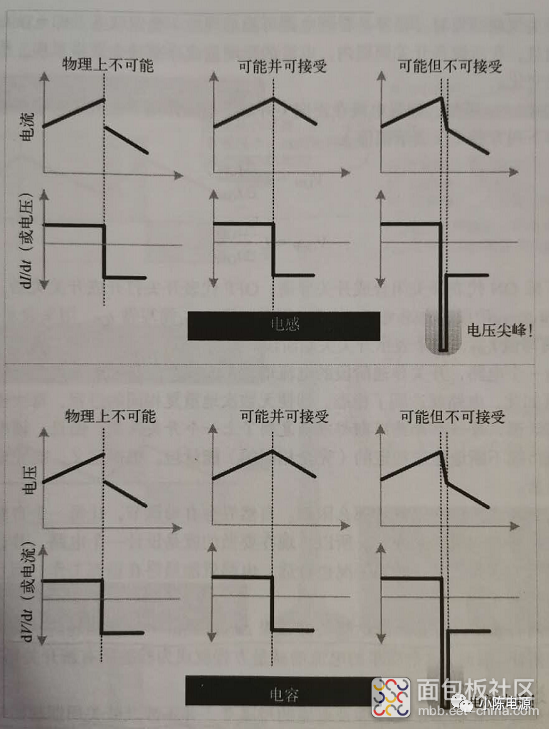
图二 电感电流不允许突变,但电感电流的变化率可以突变;电容电压不允许突变,但电容电压的变化率可以突变。
在上文中所讲述的电感电流的突变,理论上是不可能出现的,开关打开时的高压放电现象,更符合图二中“可能但不可接受”这种情况。电感放电时间就算再短,也是能够进行衡量的。当开关打开时(每次打开开关时电感电流为某个固定值时),电感电流持续的时间越短,那么电流变化率就越快,对应的感生电动势也就越大。当电感放电时间快到一定地步的时候,感生电动势的电压值就能够达到击穿空气的阈值,就能够看到开关拉弧的现象。电容短路时所产生的浪涌电流也是同样的道理。
电容电压与电容电流的数学表达式如下:
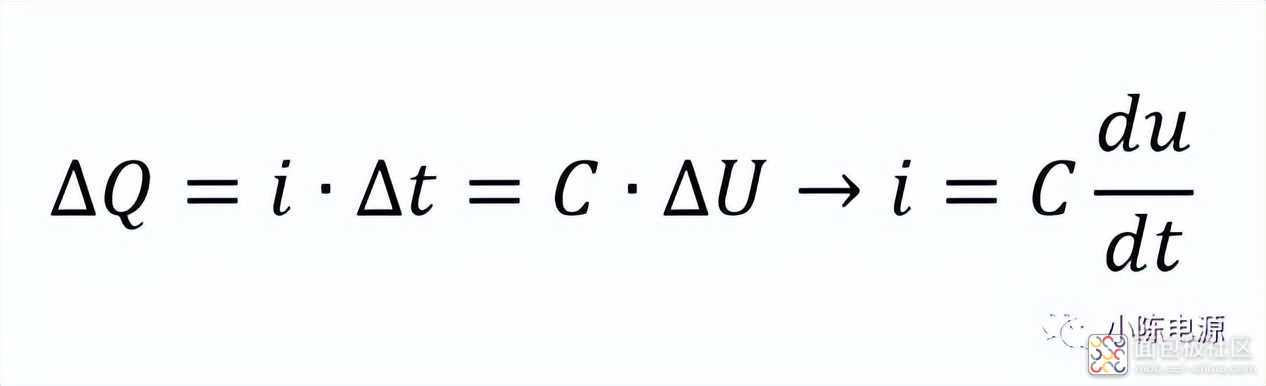
式中:
Q表示电容积累的电荷量;
U表示电容两端的电压;
来源:小陈电源







