1、一阶RC电路
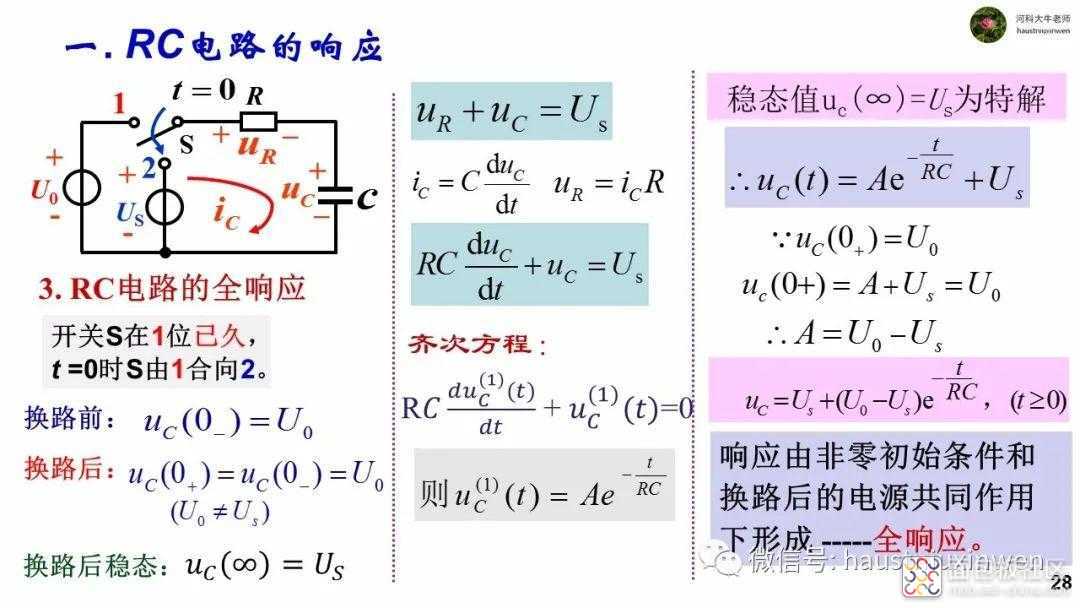
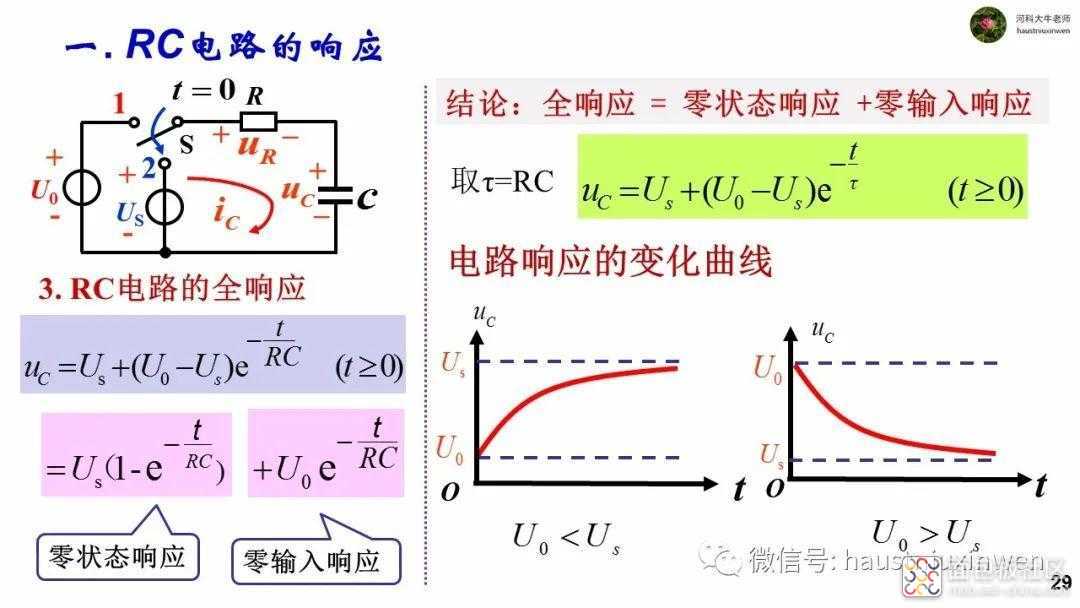
发生换路后,电路中将会存在两种能量。一是新电路中的电源,提供源源不断的电能。一是电容从旧电路中继承下来的能量。这两种能量共同推动新电路的运行,此种响应称为全响应。
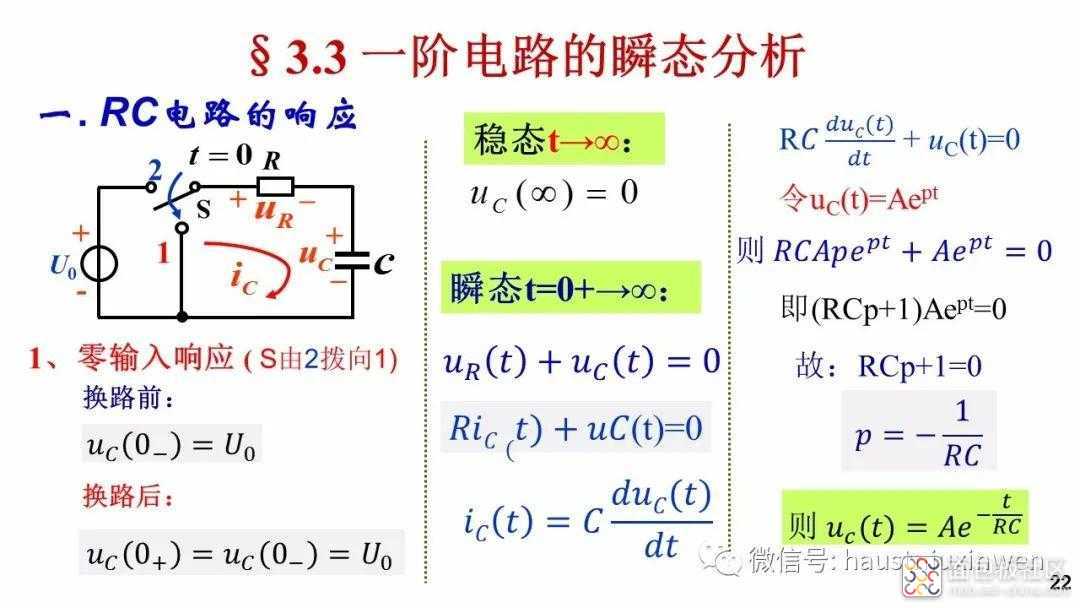
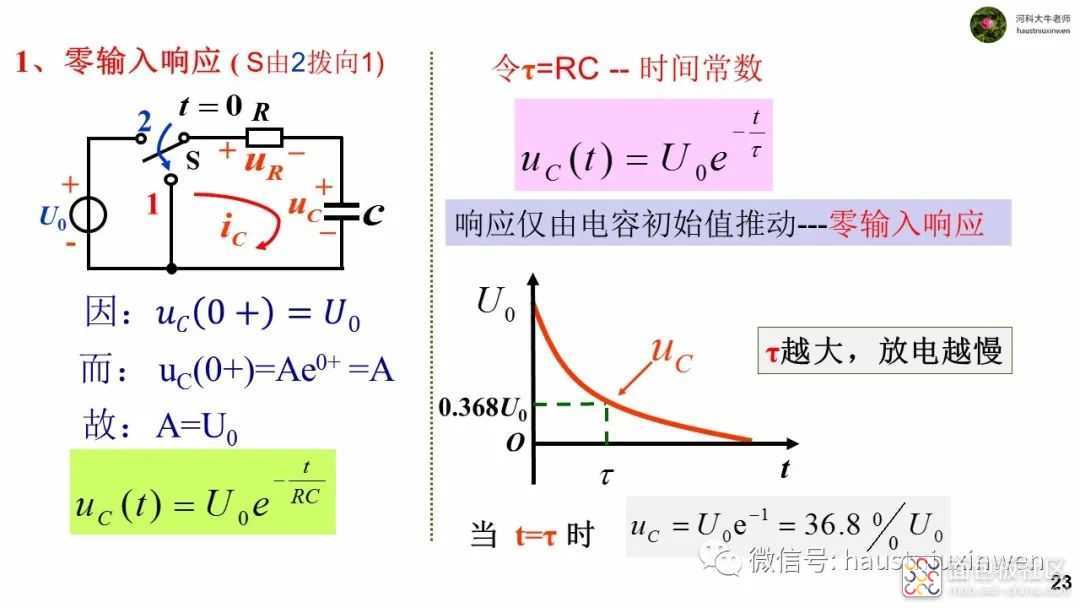
若新电路中没有电源,则只有电容储存的能量推动电路工作,此种响应称为零输入响应。由于电容中储存的能量有限,经过电阻的消耗后,将会在有限的时间内消耗完毕,最终电路中无电流,无电压。
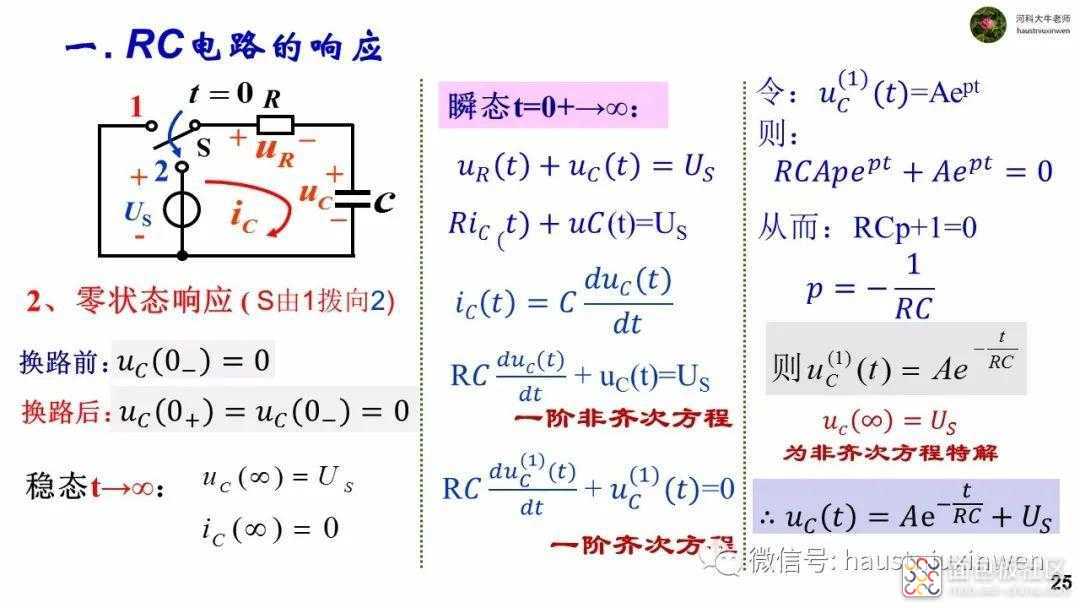
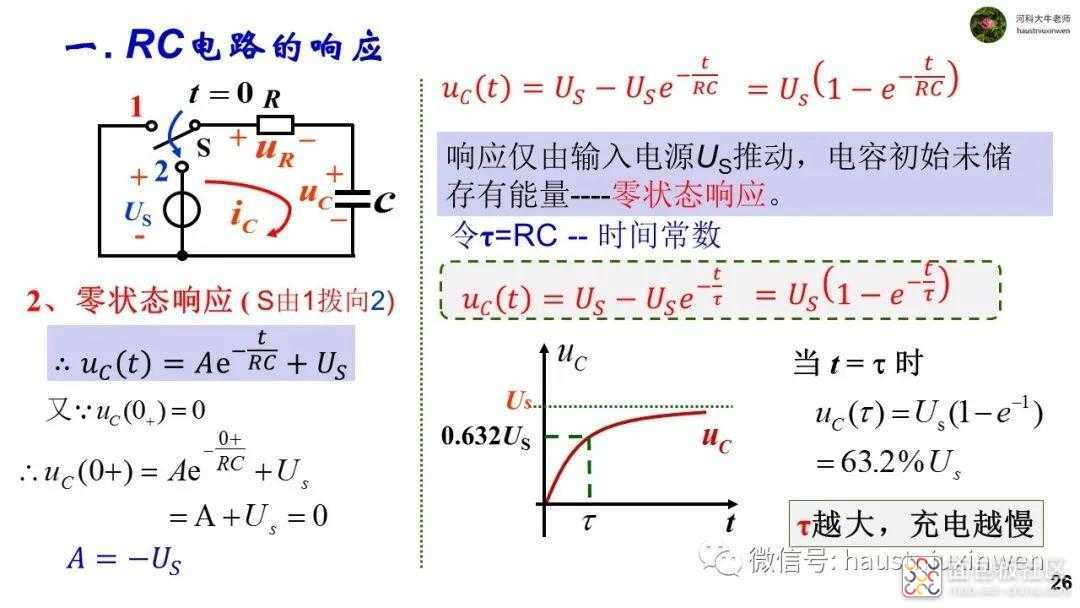
若新电路中有电源,但是电容并没有从旧电路中继承下来能量,即电容初始值为零,则新电路的工作所需能量完全来自于电源,则称此种响应为零状态响应。零状态响应表现为从零开始,经过一段时间到达一个稳定的状态,电压和电流恒定不变。
对于一阶电路而言,全响应等于零状态响应和零输入响应的和。
对一阶电路的一阶非齐次微分方程求解可得到响应的表达式,也就是瞬态响应。
从响应的组成看,响应有不随着时间变化而变化的部分,即将来的稳定值,也有随着时间而逐渐减小,最终消失的部分,这两部分分别是由电源和电容储存的能量推动。
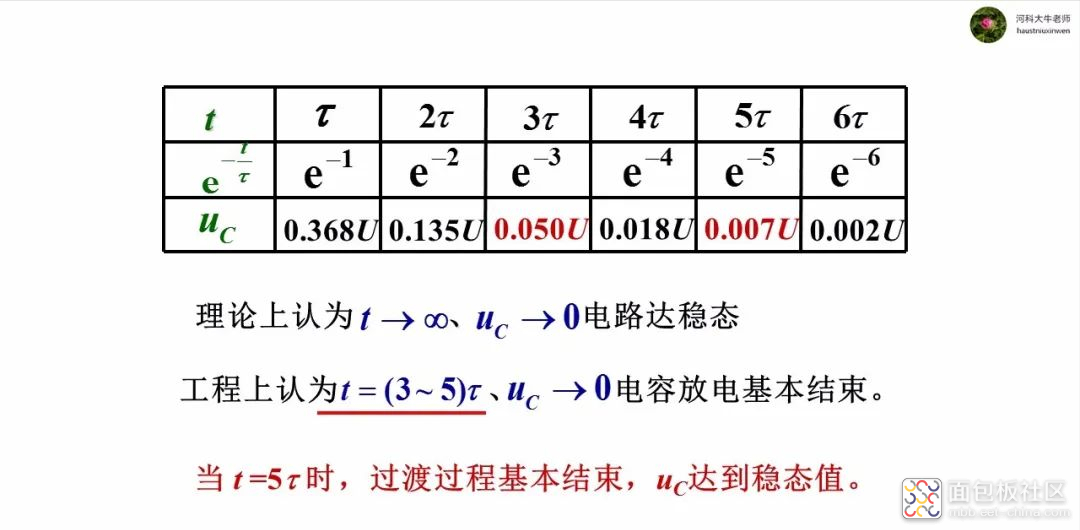
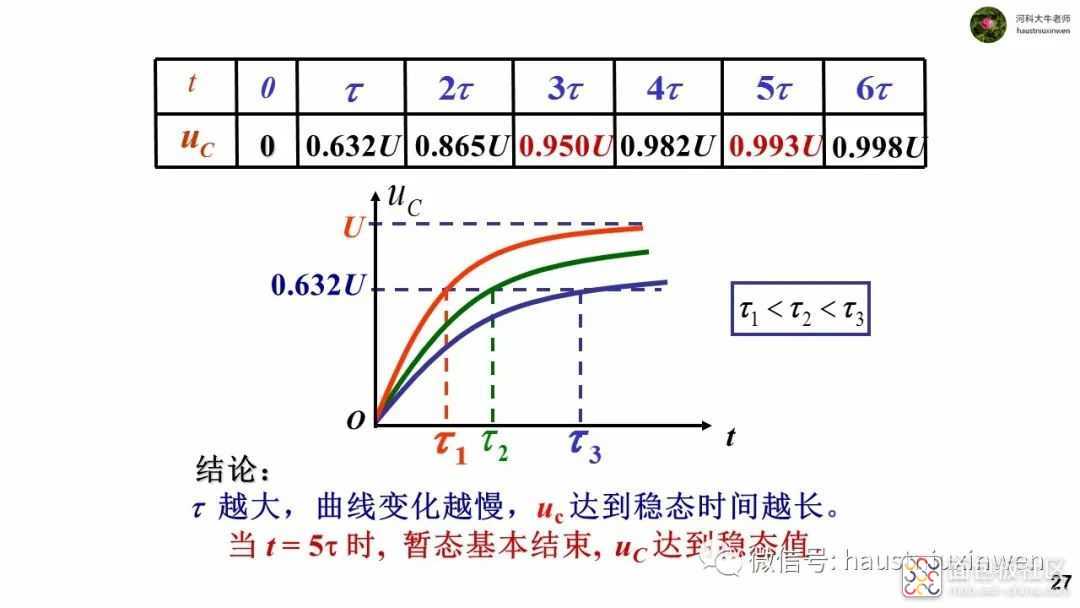
从响应的表达式看,过渡部分是按照指数规律逐渐衰减的,衰减的快慢取决于RC的乘积。大概(3~5)RC时间后,衰减为零,即过渡过程结束,达到稳态。令τ=RC,称为时间常数。
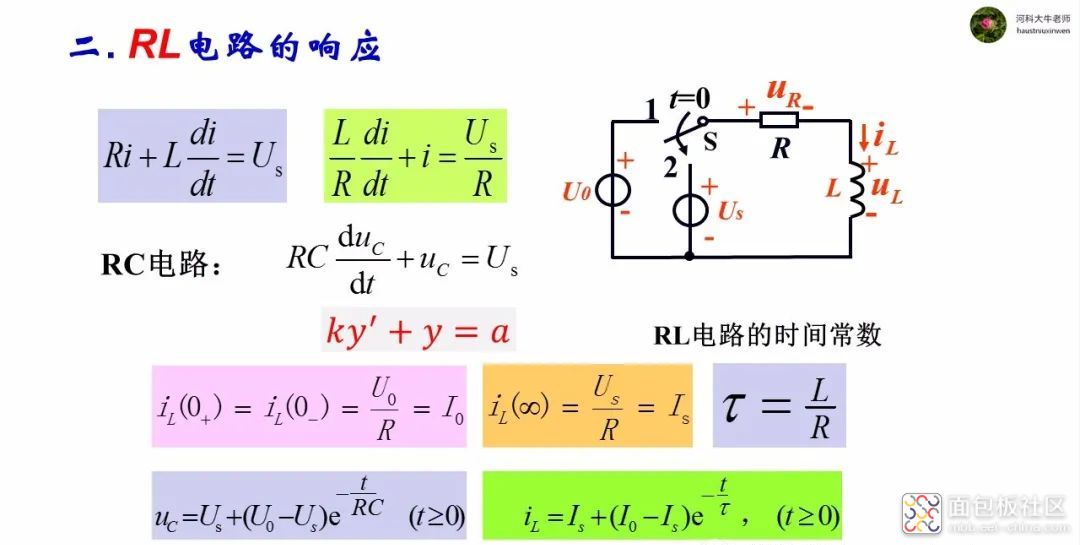
2、一阶RL电路
一阶RL电路有着和一阶RC电路相同的电路模型,区别是以电感电流为自变量。因此电感电流和一阶RC电路中的电容电压有着相同的表现。
电感电流的全响应等于零输入响应和零状态响应的和,暂态部分也是按照指数规律衰减,衰减速度取决于时间常数τ,(3~5)τ后,过渡过程结束,达到稳态,只是其中的τ=L/R。







 /3
/3 
