概述
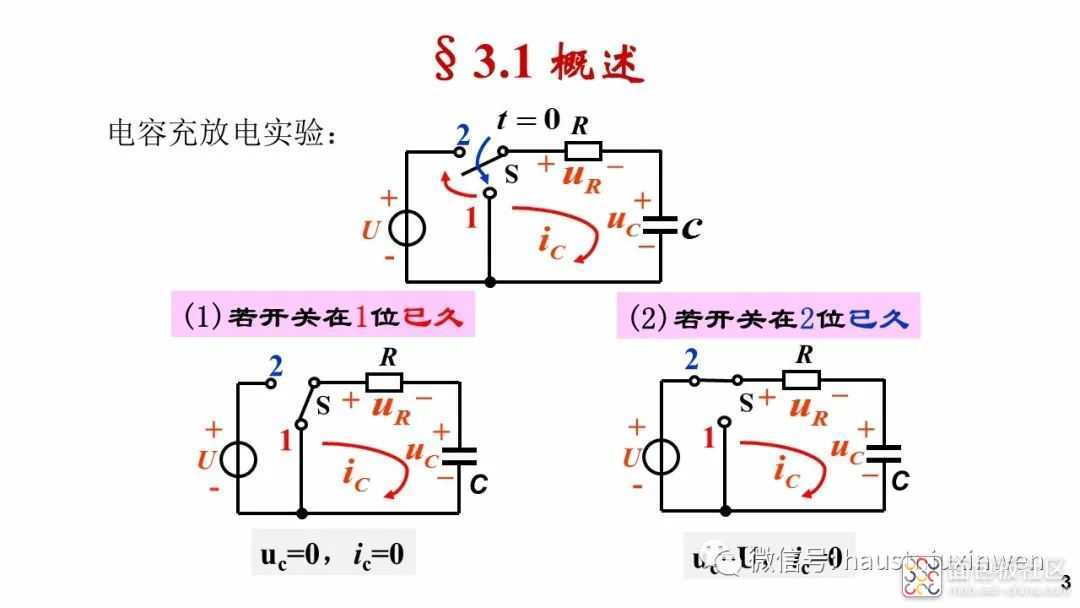
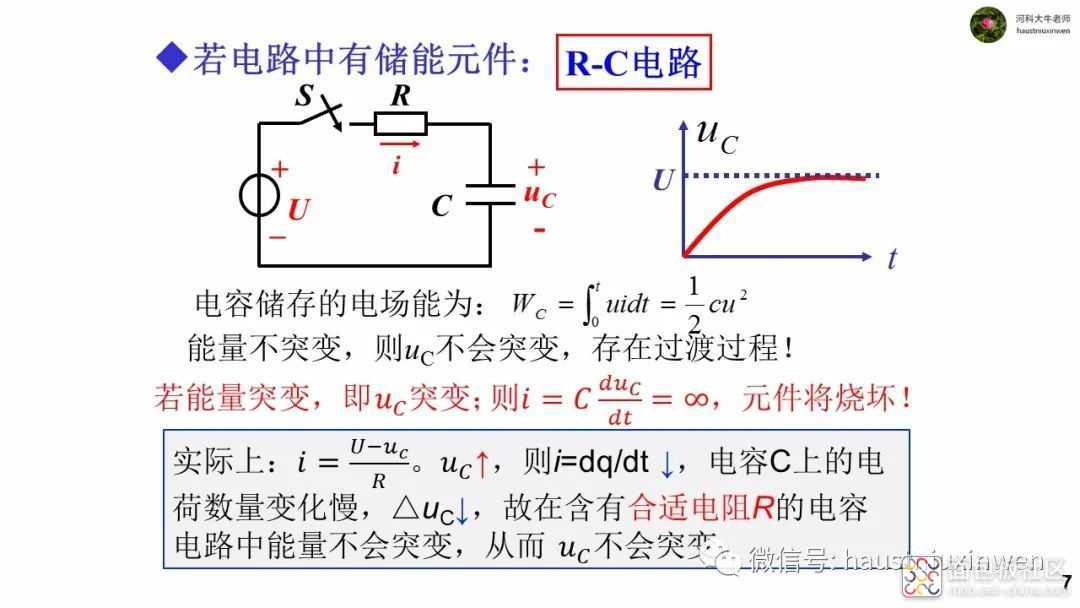
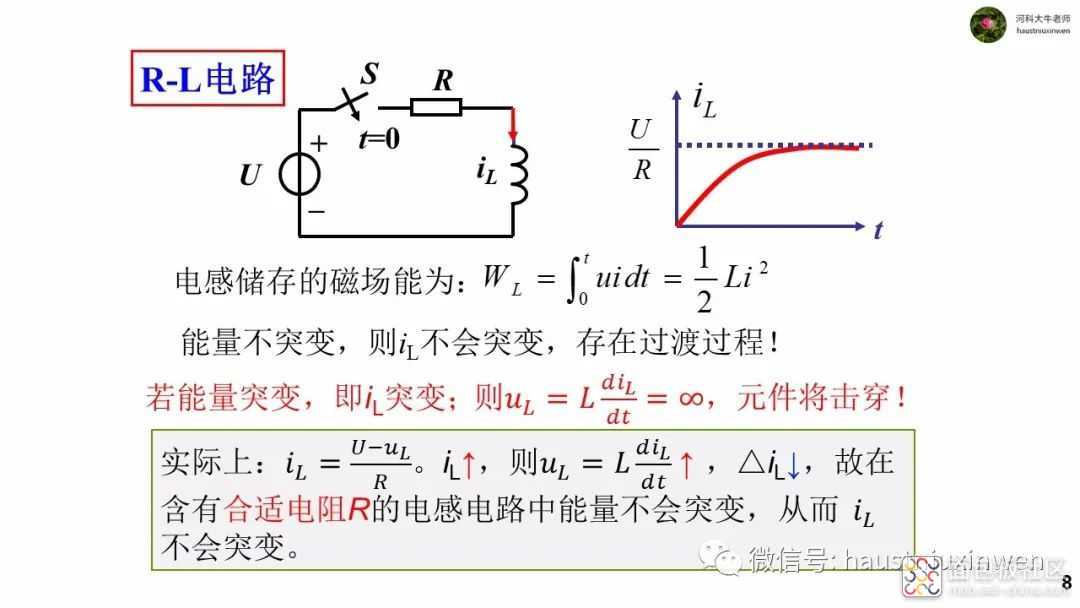
当电路中存在电容或电感时,若电路中存在变动状况,比如开关的开合,参数的波动等,则电容和电感的电压和电流也会发生变化。
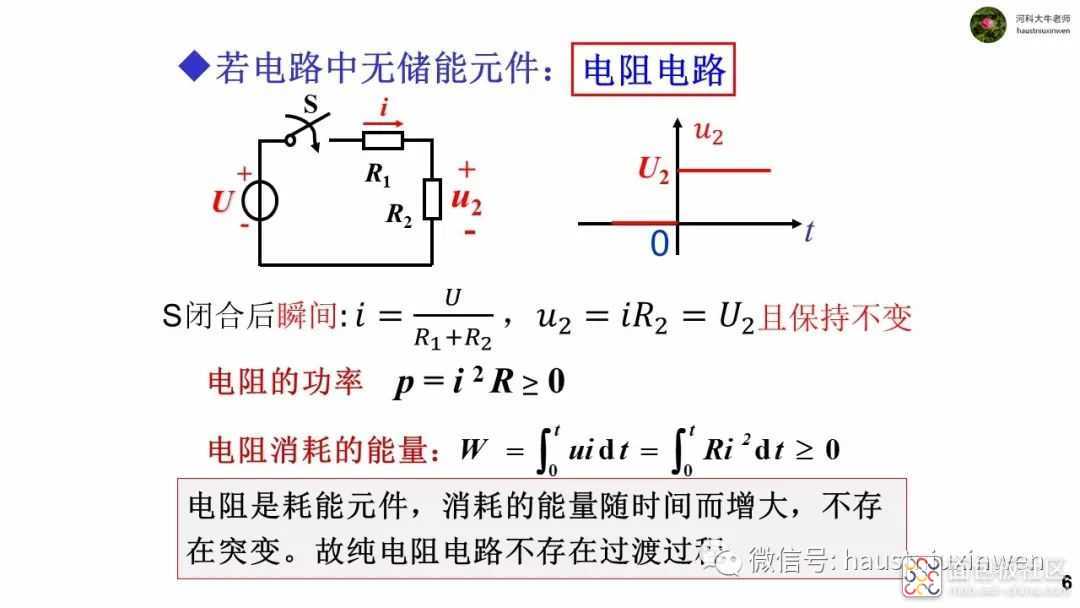
对于电阻而已,电压和电流之间永远保持一个固定比例值,即阻值R。因此当电压或电流变化时,对应的电流或电压按照固定比例变化,两者波形完全相同,可以说电压和电流是同步变化的,没有任何时间上的延迟。
与电阻不同,电容和电感均为动态元件,其电压和电流之间的伏安关系不是简单的比例关系,而是微分关系,从而造成了在变化的电路中,电压和电流的变化会有时间上的超前或延迟,并不同步,电压和电流的波形完全不同。
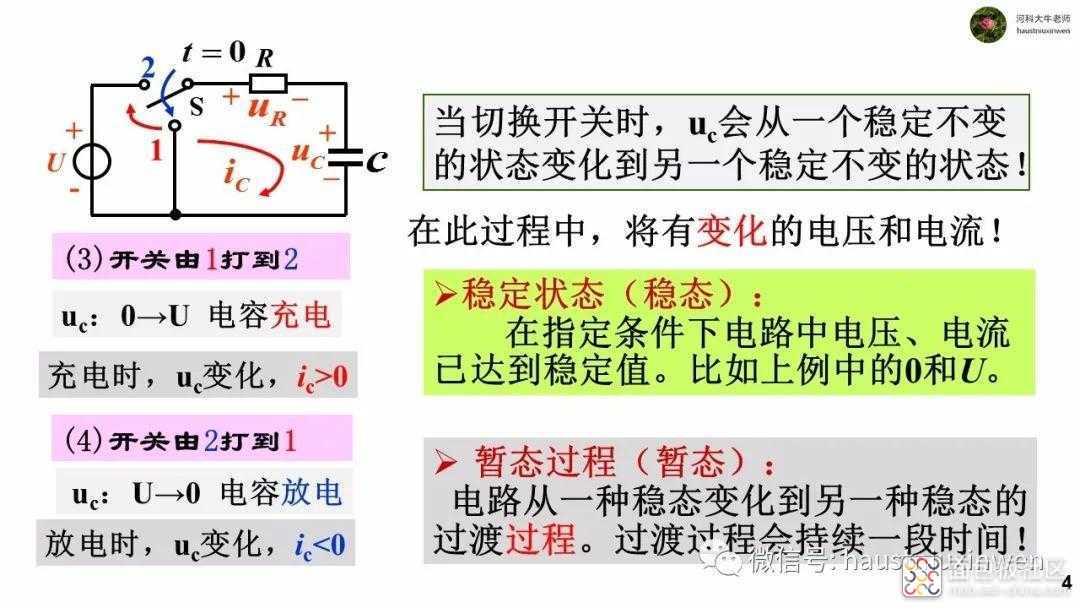
若电路发生换路,并且换路后的电路在很长时间内不再发生新的换路时,电路将会变化到一个稳定不变的状态,所有电压和电流均不再变化。
我们把刚刚发生换路后的瞬间电压和电流称为初始状态,经过足够长时间后达到新的稳定不变的状态称为稳态,从初始状态到稳定状态中间的这一段称为过渡状态。
本章的任务就是要弄清楚,发生换路后,初始值和稳态值的具体数值,初始值按照什么规律变化到稳态值,又需要经过多长时间达到稳态,即过渡过程结束。
初始值和稳态值
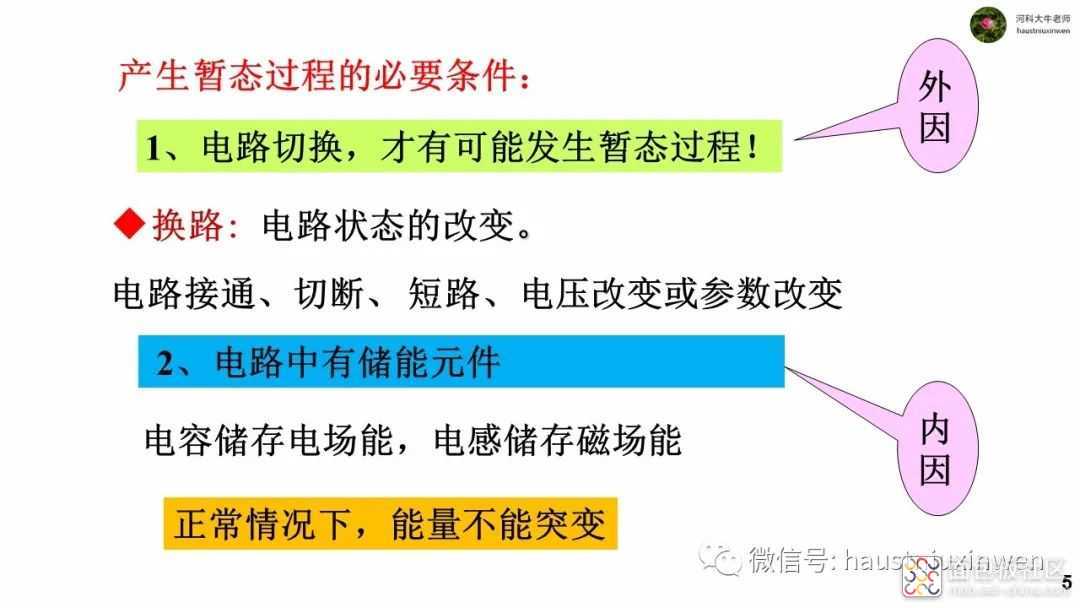
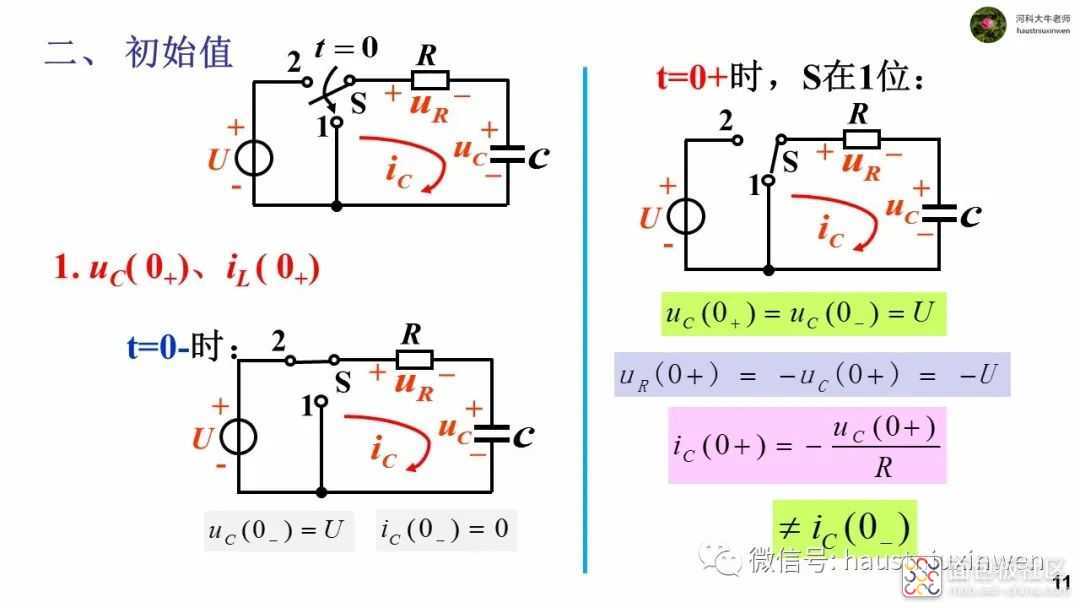
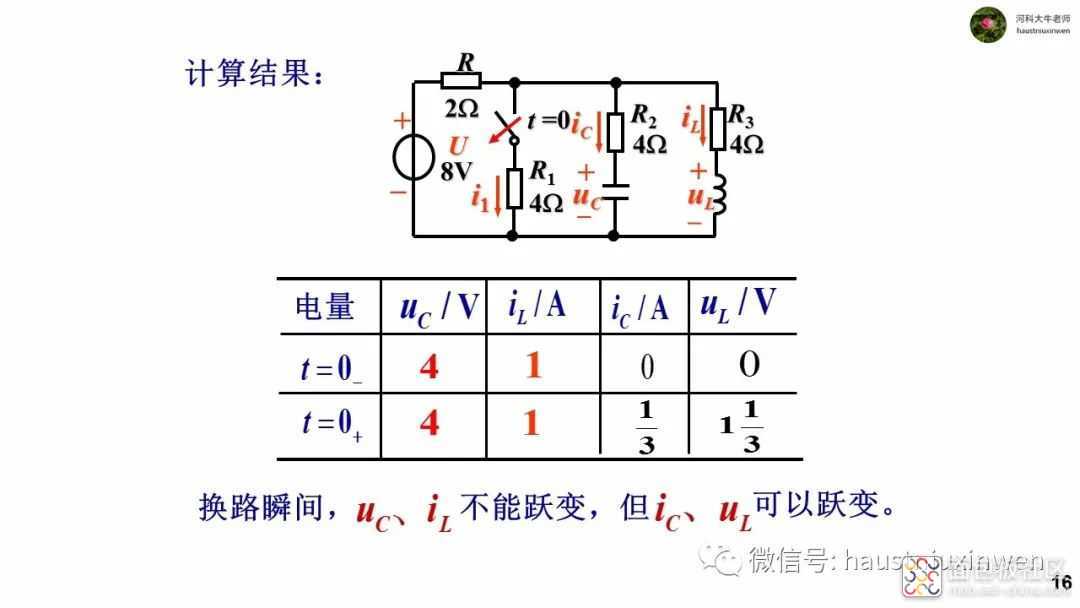
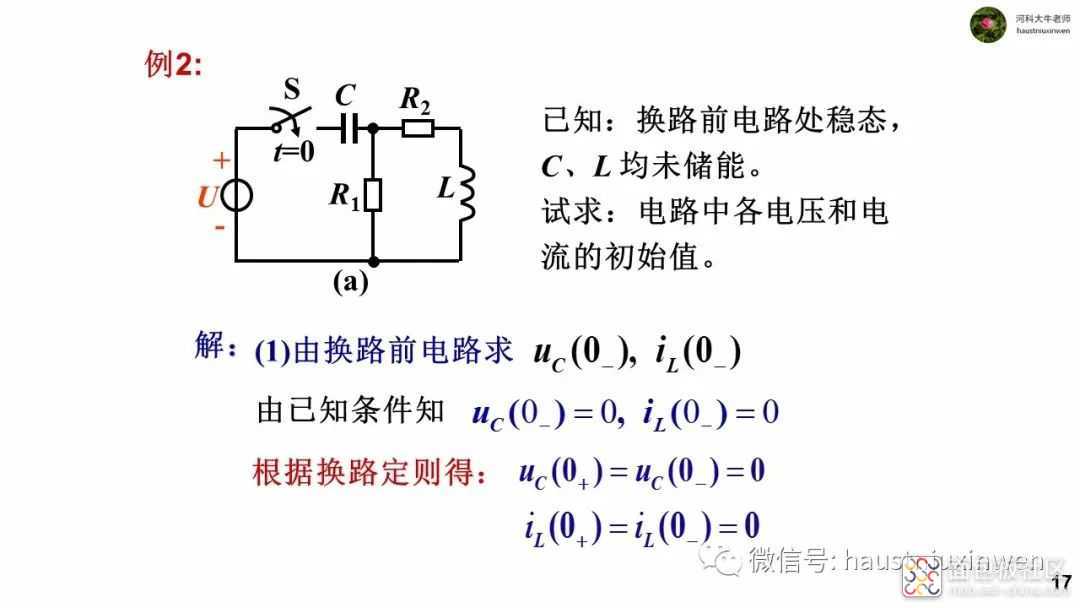
当电路发生换路时,由于能量不能突变, 即存在电容上的电荷和电感中的磁场能量不会突然消失或者突然增加,造成在换路的瞬间,电容电压不变,电感电流不变,即uc(0+)=uc(0-),iL(0+)=iL(0-)。
(需要说明的是,若电路中没有电阻,或者电阻极小,也可以发生突变,突变的结果是电路烧坏元件。比如强行用一根导线短路充满电的电容,能量突变,导线或电容将烧坏。)
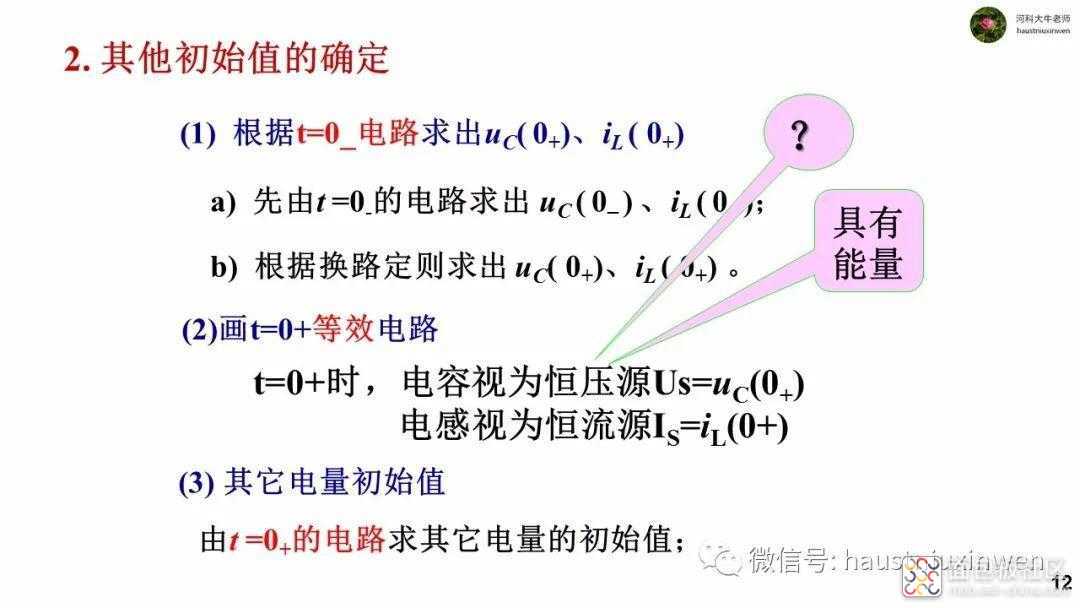
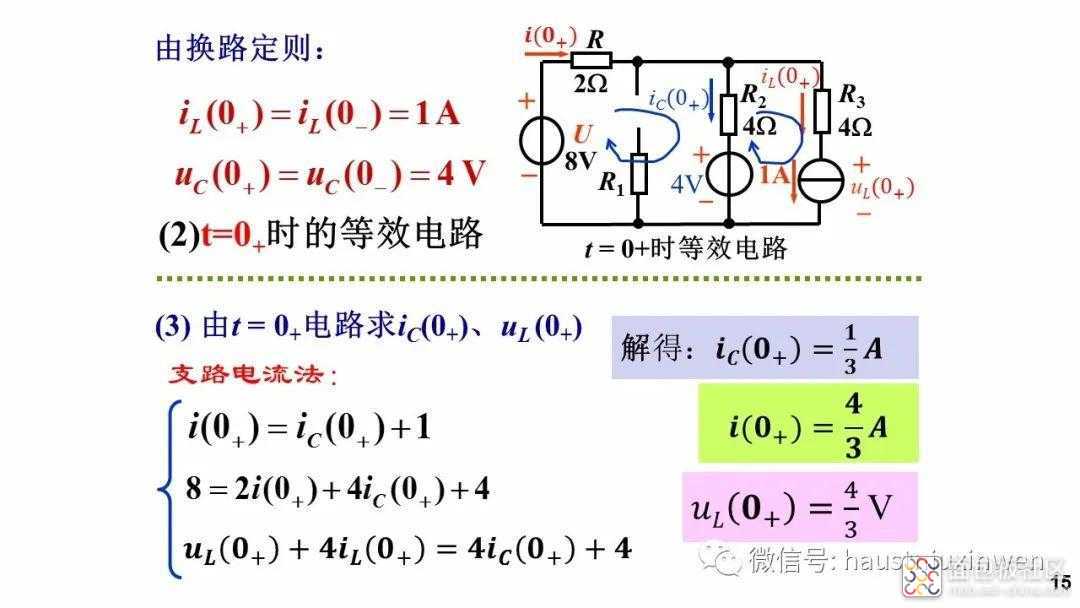
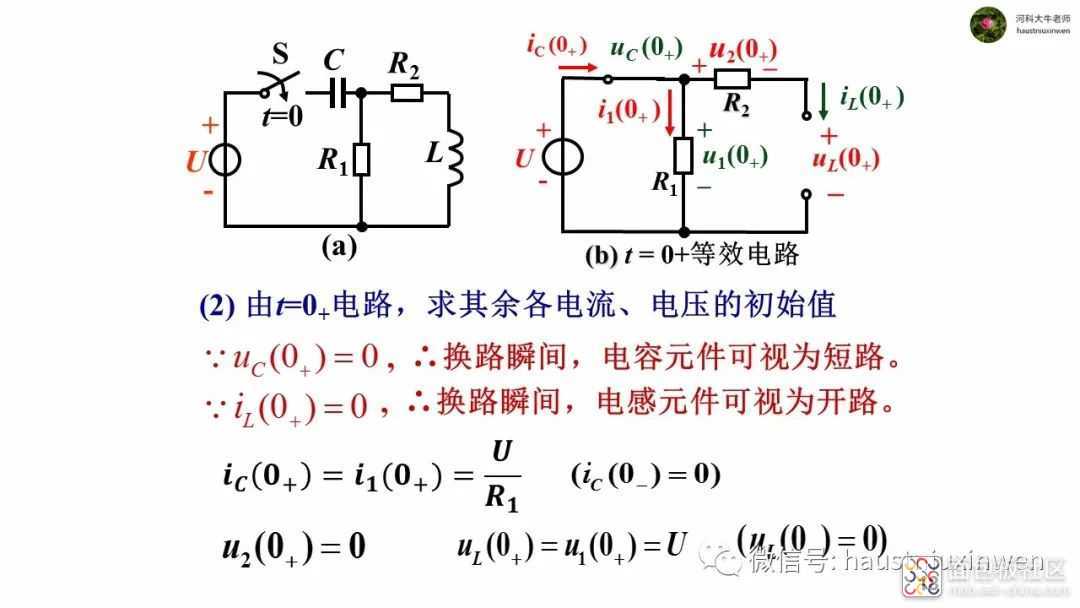
注意, 换路瞬间,只有电容电压和电感电流这两个量的数值不会发生变化,而其他电压和电流是可以突变的。此时欲获取其他电压或电流的初始值时,需要绘制出t=0+时刻的电路, 然后用支路电流法或结点电压法来求取。
在换路的瞬间(t=0+时刻),由于电容和电感具有能量,且不会突变,故会对电路产生和恒压源、恒流源相同的作用。因此,在求解其他电压和电流的初始值时,应该将这两个元件视作恒压源和恒流源,这一点要在绘制t=0+等效电路时注意。
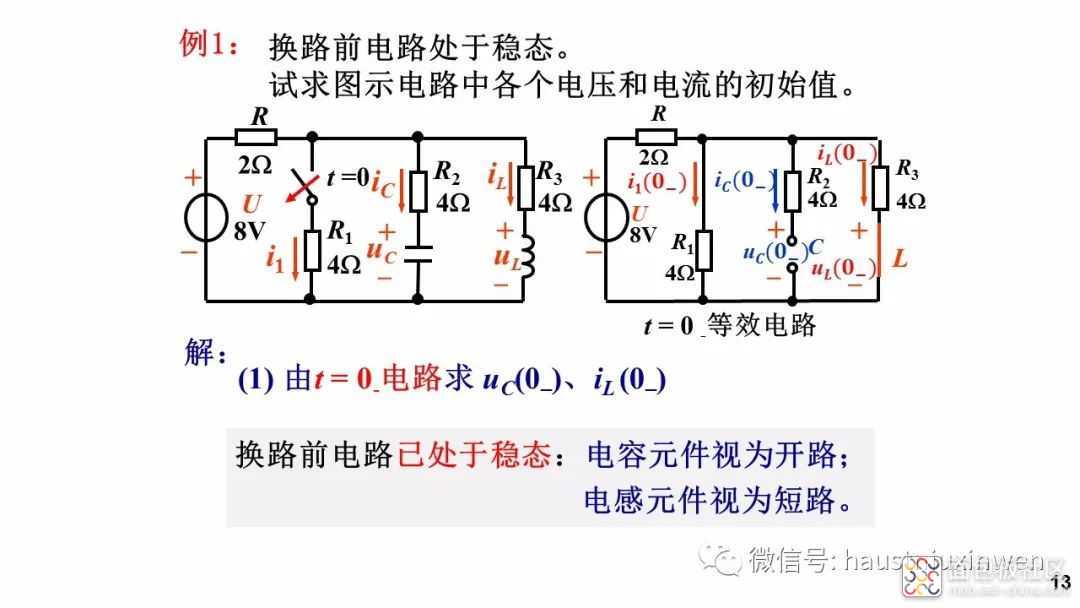
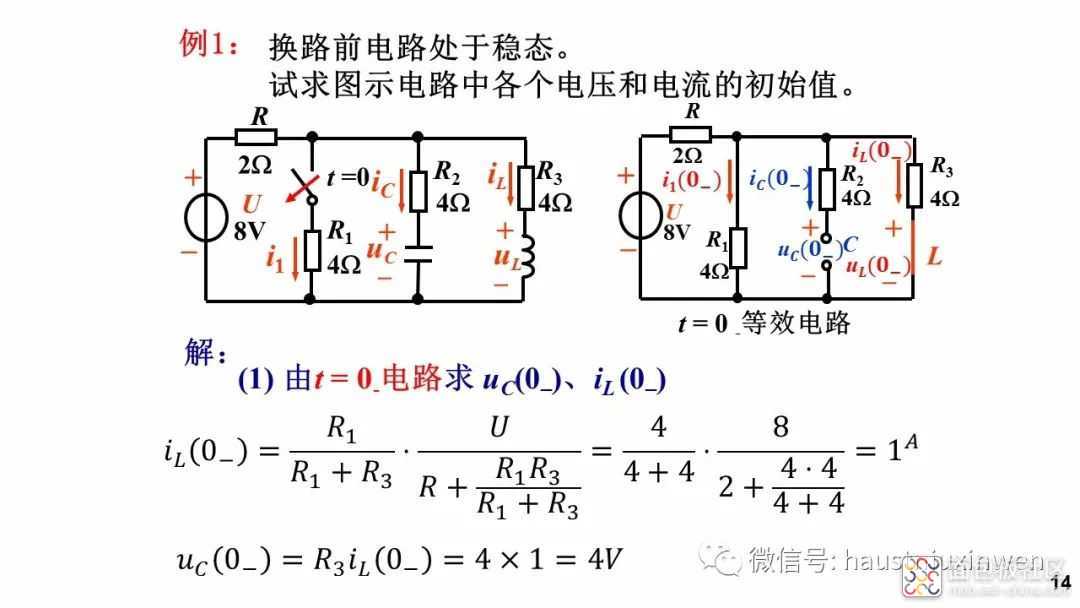
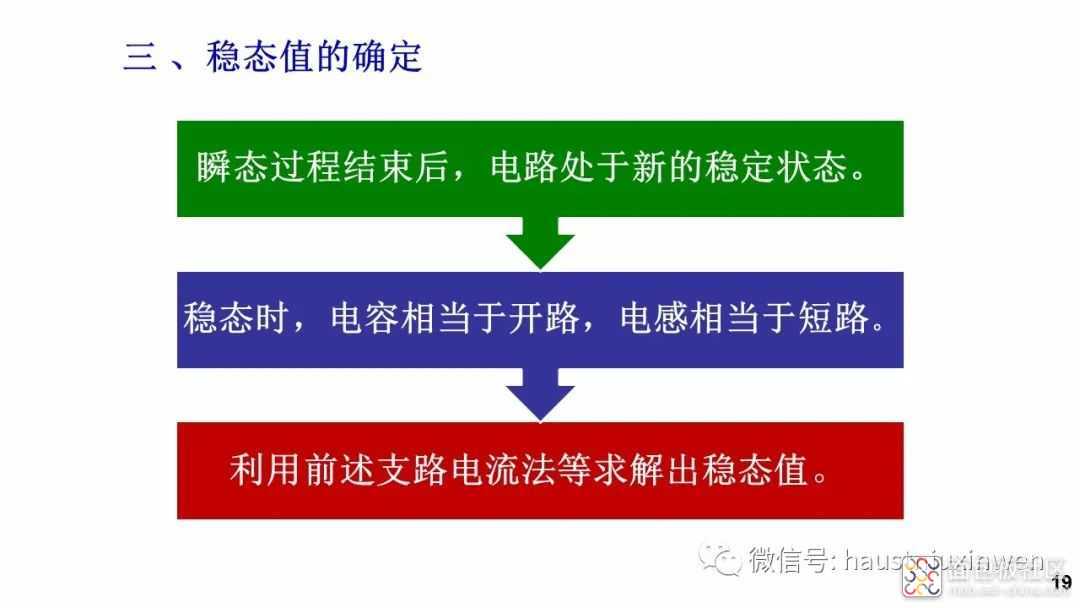
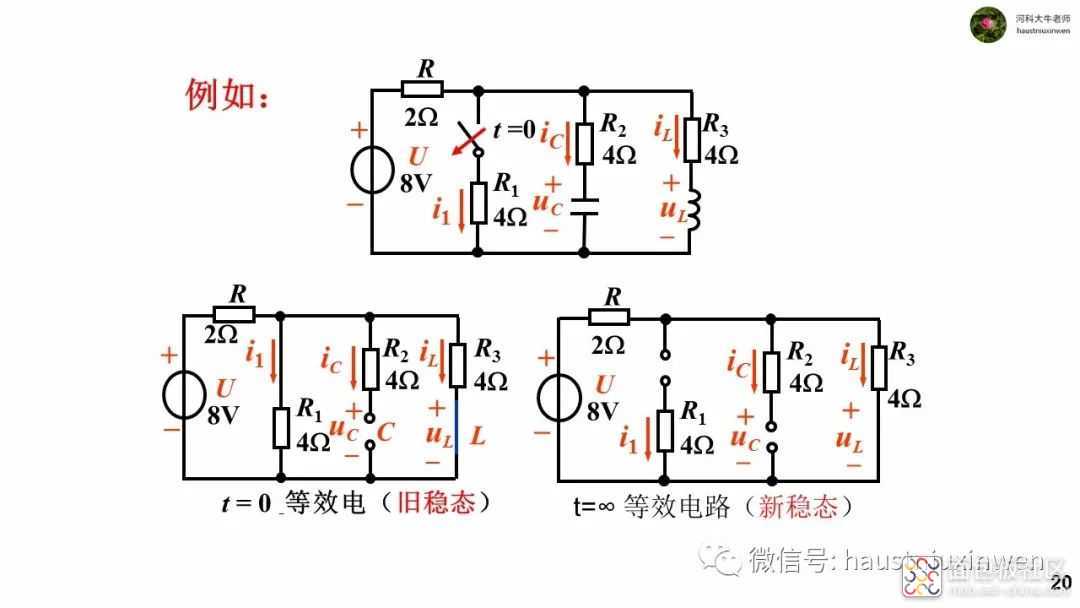
当电路发生换路后经过足够长时间,电路达到稳态时,所有的电压和电流不再变化, 则电容电压不再变化,电流等于零,相当于开路;电感电流不再变化,其电压为零,相当于短路。









 /1
/1 

