在第二部分中,我们看到涉及时间的卷积,其中数字序列的索引是时间索引,以及所涉及函数的自变量。像往常一样,我使用网络上的公共材料。
我们只考虑 线性系统,但它们也是 时不变的 或 (LTI = 线性时不变),即不随时间改变其行为。
我们特别关注那些提供 输入函数 x(t) 和 输出函数 y(t) 的LTI 系统 ,这些函数通过所谓的 传递函数 = 输出函数 / 输入函数链接在一起。原则上,传递函数可以用多种方式表示。
时间函数的传递函数定义为 脉冲响应 (RI) , 通常写作 h(t) = 输入产生的输出 x(t) = 单位脉冲。一般响应 y(t),即输出,原来是 输入和 RI 之间的卷积,写为 y(t) = x(t)*h(t)。
奇怪的糕点店作为简单直观的演示,让我们考虑一个在网络上找到的有点奇怪的示例 ( https://www.youtube.com/watch?v=aEGboJxmq-w )。假设我们知道一家 面包店以自己的方式出售曲奇,那就是:如果你有一天给她一美元,她第二天会给 你送 一块 曲奇,然后在第三天送另一块 曲奇。换句话说,糕点店遵循自己的程序(schedule):可能如下:

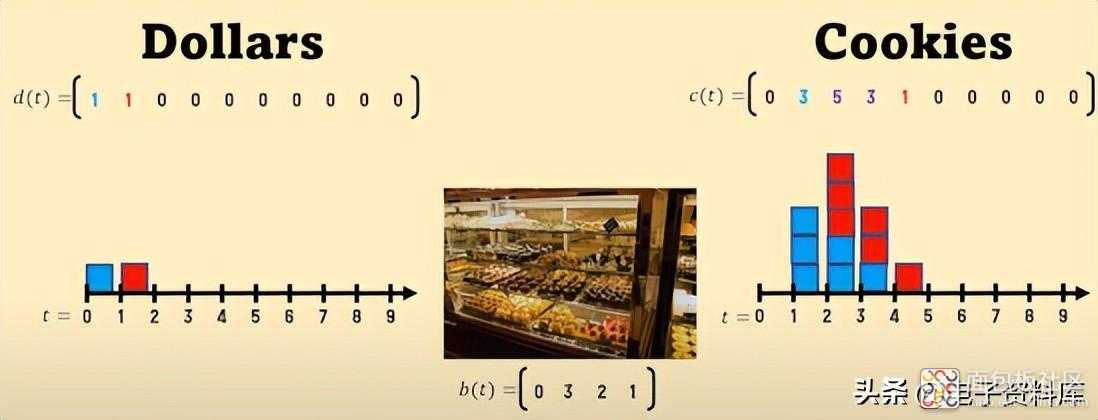
实际上,这个过程 并不像从图中看起来那样与一周中的特定日子相关联 ,而是一般性的。然后让我们将它安排在时间轴上,其中 突出显示三个序列作为 每天发生的 时间的函数,在例如 10 天的跨度内:
d(t) [ dollars ] 以美元为单位的每日输入
c(t) [ cookies ] cookie 数量的每日输出
b(t) [ bakery ] 输入和输出之间的链接,典型的每个面包店,当输入 = 1 时,我们可以称之为“脉冲响应”:因此,最初,c(t) = b(t)。
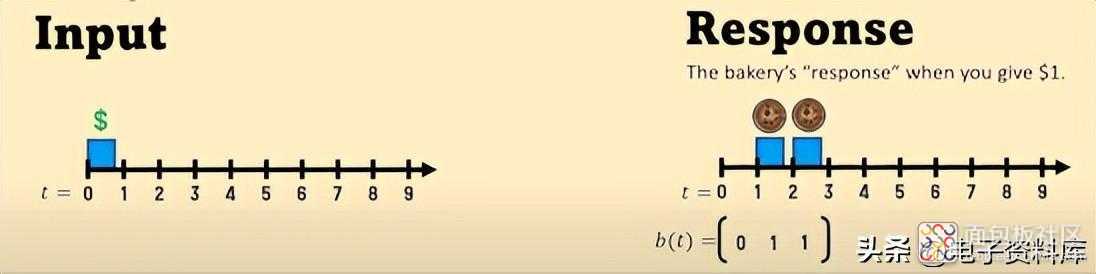
但不仅仅是最初,因为每当 d(t) = 1 时,答案 c(t) 总是 = b(t)
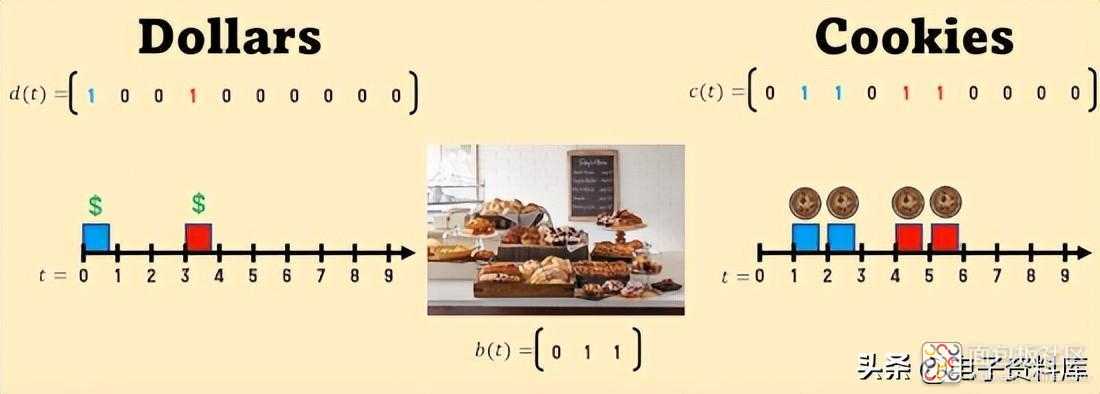
如果我们假设糕点店不会随时间 改变“政策”,我们就会发现自己处于LTI 情况
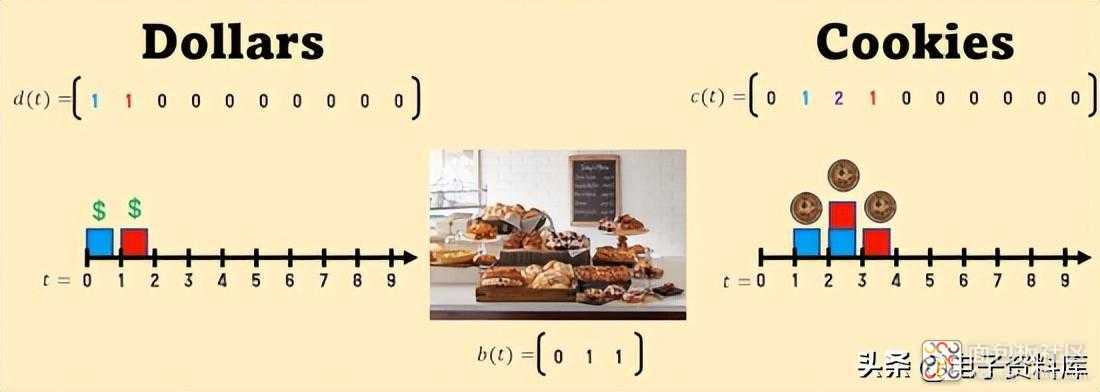
因此,如果在输入中我有两个数字中指示的美元,则在输出中 cookie 也将是指示的那些,因为它们 只是相加。
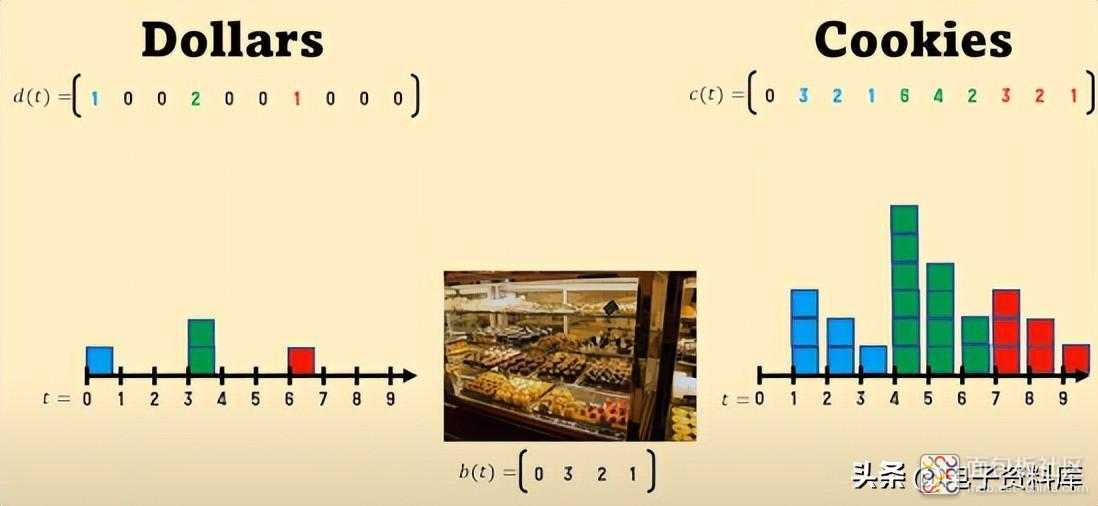
另一家糕点店现在我们决定去 另一家糕点店,它有 不同的政策,由其 RI描述 ,即由其 b(t) 描述。这些图显示了 3 种输出情况对应于同样多的输入情况,仅由 b(t) 确定。
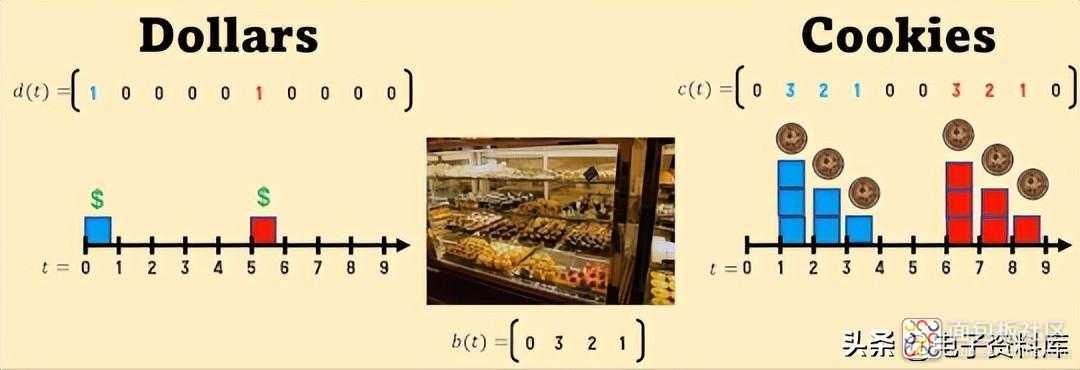
一点点数学是不可避免的
在这种情况下,输入和输出之间的数学联系是什么?由于我们处理的是 时间上的线性运算,因此可以将它们转化为 以“ t ”为单位的线性方程组,这些方程由多项式组成 ,其次数随着随后每一天的增加而增加,方程和未知数与天数一样多正在考虑。
然而,更通用和更有用的方法是使用向量和矩阵。像往常一样,我们在这里处理数学概念时没有要求它们具有数学严谨性,因为我们感兴趣的是该主题的直觉方面。
3 个序列 c(t)、b(t)、d(t) 可以用向量表示 。在下面的示例中,c(t) 和 d(t) 跨越 7 天,即它们是 7-component vectors。
脉冲响应是一个包含 4 个分量的向量,这意味着其余分量的值 = 0。
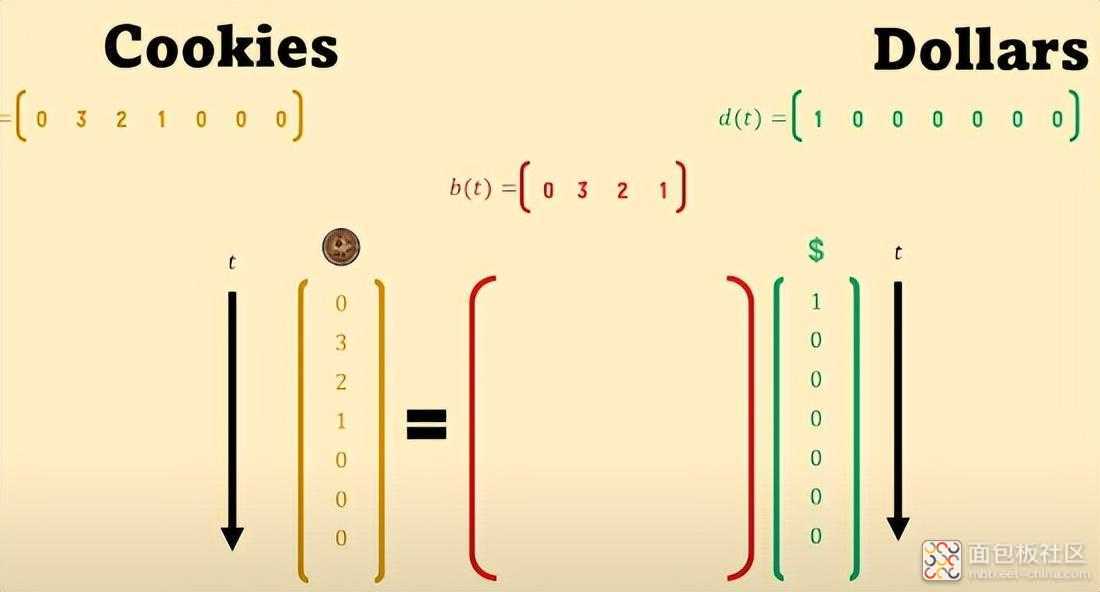
为了阐明所寻求的链接,让我们一步步进行。
如果 d(t) 是一个“ 单一脉冲”,即第一天只有 1 美元,c(t) 会回复 b(t),然后根据需要添加尽可能多的零来填充向量 b(t) 的分量。
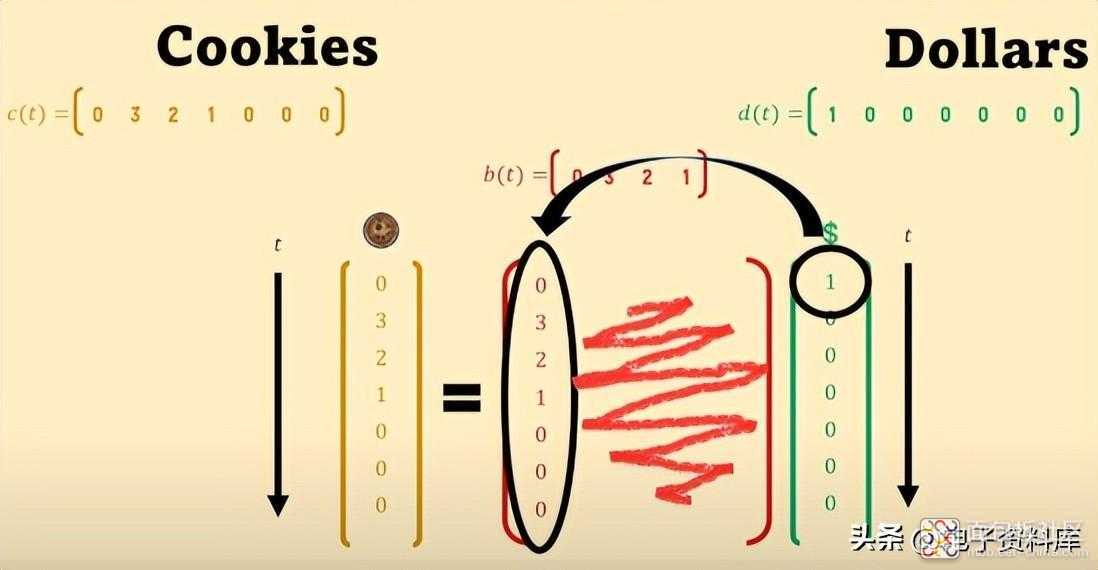
如果孤立的美元进入 第二天,饼干也是如此;c(t) 包含 b(t),但移动了一天,因此它的向量有两个初始零点和两个最终零点,并沿着前一个向量 b(t) 开始填充将成为矩阵的内容。
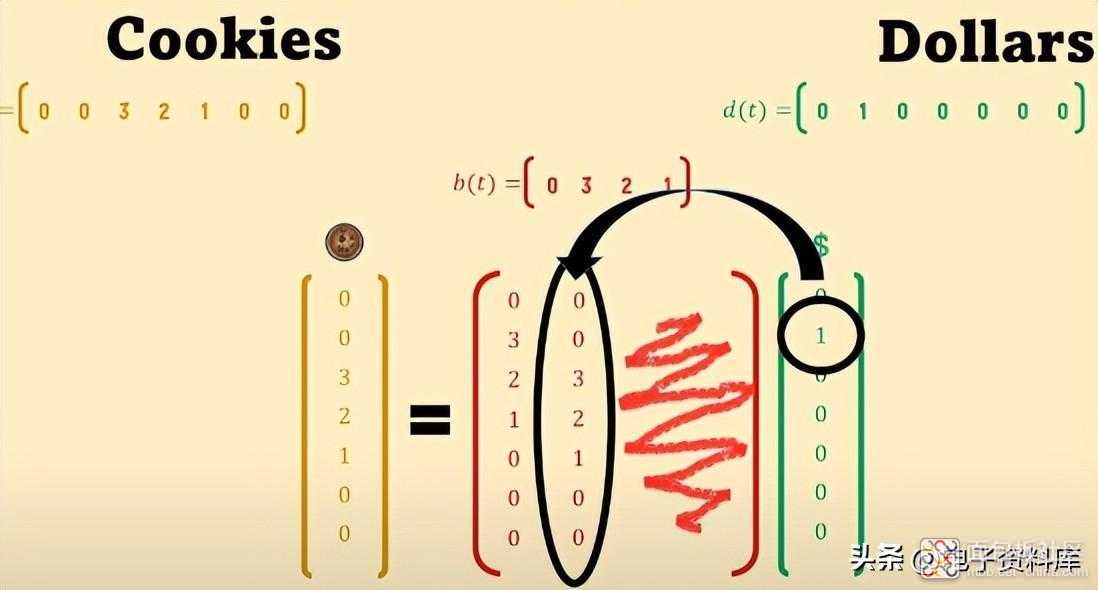
如果每天移动孤立的美元,也会发生同样的情况。
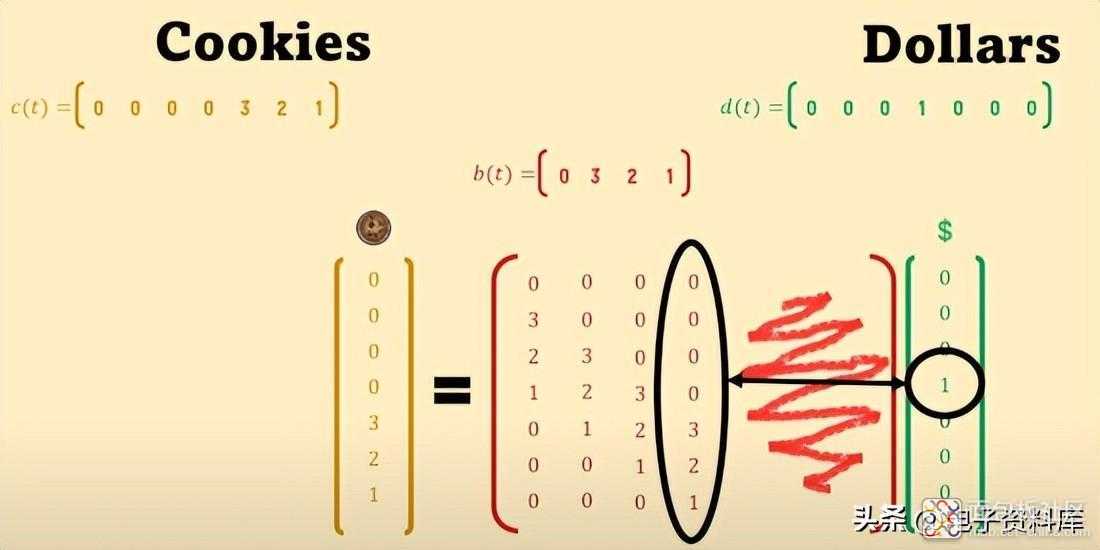
在某些时候,我们达到了最终情况,在这种情况下,我们填充了矩阵 ,该矩阵将简单地乘以向量 d(t)(我们需要记住如何乘以矩阵...):
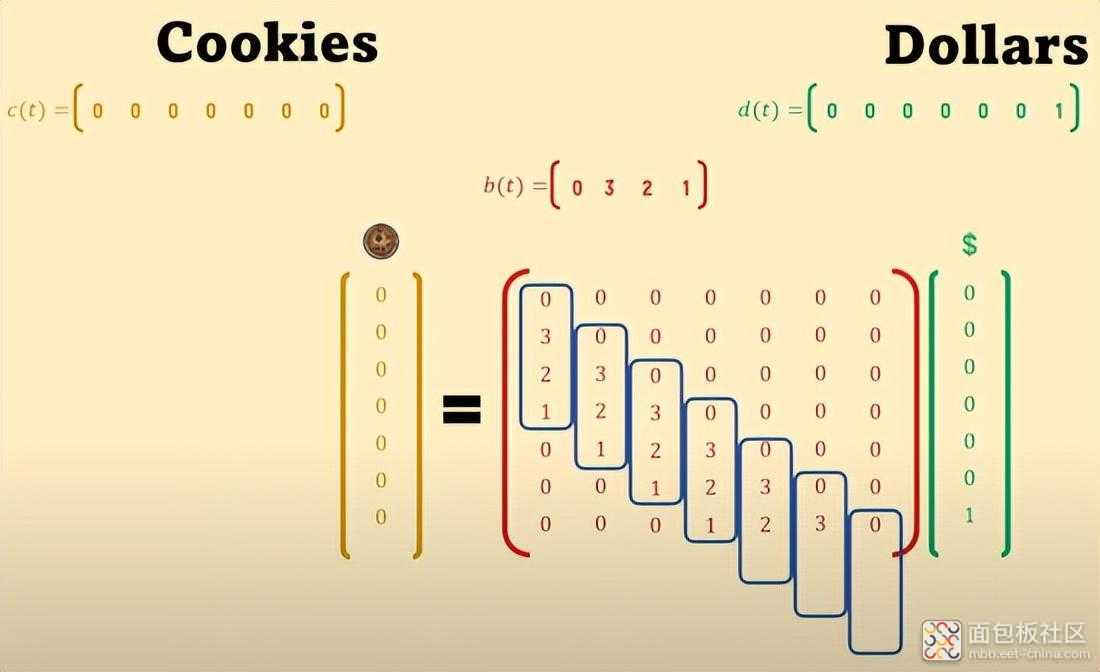
查看 矩阵,可以看到占据 矩阵 列的连续脉冲响应 b(t) 如何 随着时间的推移从左到右向下移动。但我们也看到 同样的 事情 发生在 矩阵的行上:
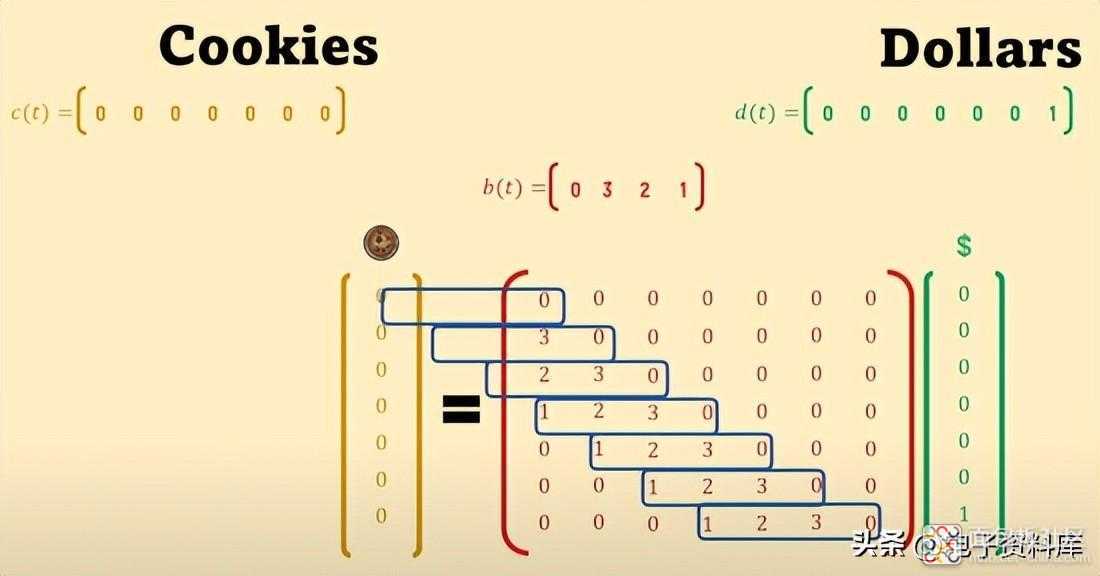
还可以看出序列 b(t) 如何在矩阵中“反转”,相对于开始时定义的脉冲响应 b(t)。
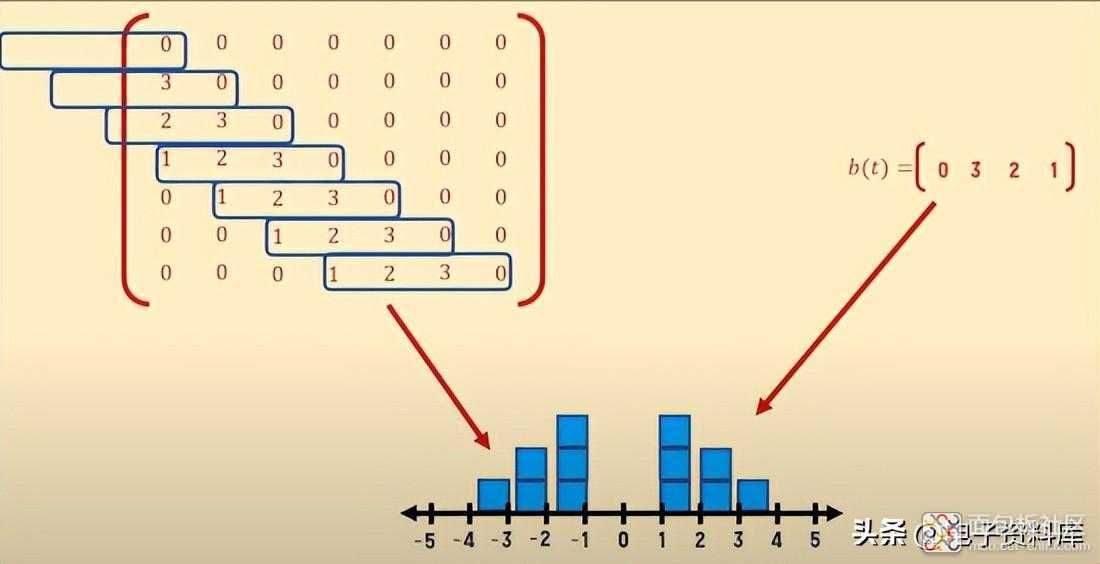
想概括一下,报告向量和矩阵中根据时间索引排列的值很方便:

实际上图中表示的是 矩阵的乘积 (第二个矩阵仅由单列组成,即它是一个向量), 目前 也用于表示 线性方程组的模态。
矩阵的乘积要求第一个矩阵的列数与第二个矩阵的行数相同(在本例中只有一列)。结果是一个矩阵,其中 第i 行和第 j 列的每一项是 每 行 i 和每 列 j的点积 (这里只有 j=1)。
在检查的情况下,矩阵中的时间从左到右 , 从上到下流动,但我们立即看到表达式 b(- (tt)) 是不可接受的。时间永远是时间,但是这里我们要区分流逝的时间和已经流逝的时间,把它当作 另一种时间来对待。

这是通过调用τ 从左到右“流动”的时间来完成的,即 与单个事件的记忆相关的 时间从上到下它仍然被称为t。实际上,在每个时刻 t,输出值是通过滑动时间 τ来计算的。
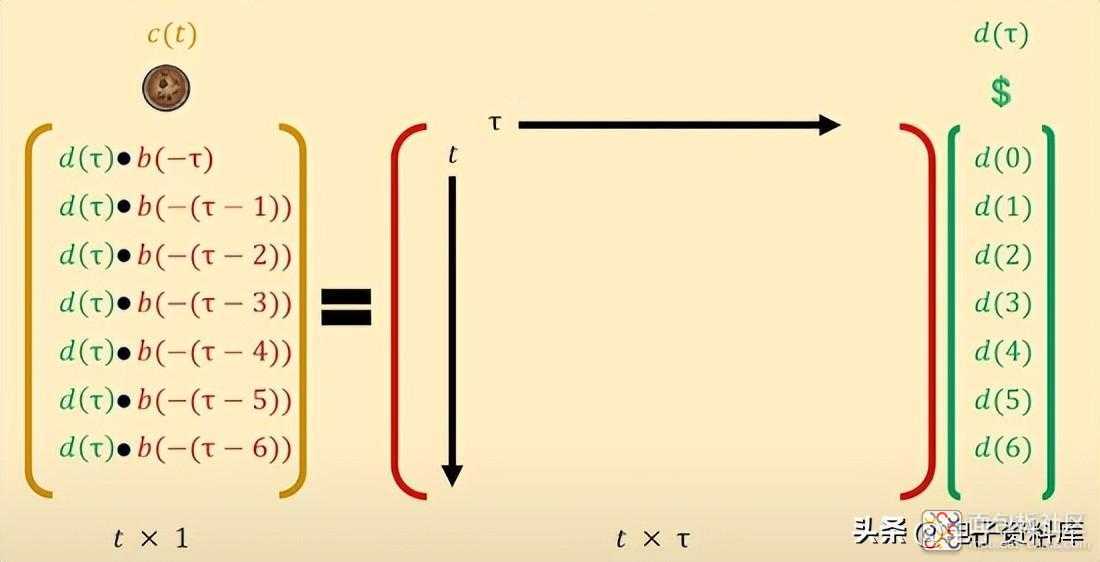
回想 糕点店,我们看到它给我们的糖果不仅是当天支付的结果,而且还包括之前支付的结果,因为糕点店的政策是长期有效的随着时间的推移,需要“系统内存”。
因此我们得到了一个 非常简洁的写作,它突出了点积作为矩阵乘积的一个特殊情况(假设结果只有一列)。

显式标量积:
c(0) = d(0)b(0)
c(1) = d(0)b(1)+d(1)b(0)
c(2) = d(0)b(2)+d(1)b(1)+ d(2)b(0)
c(3) = d(0)b(3)+d(1)b(2)+ d(2)b(1) + d(3)b(0)
c(4) = d(0)b(4)+d(1)b(3)+ d(2)b(2) + d(3)b(1)+ d(4)b(0)
c(5) = d(0)b(5)+d(1)b(4)+ d(2)b(3) + d(3)b(2)+ d(4)b(1)+ d(5)b(0)
c(6) = d(0)b(6)+d(1)b(5)+ d(2)b(4) + d(3)b(3)+ d(4)b(2)+ d(5)b(1)+ d(6)b(0)
因此我们得出了离散卷积 的最终公式 。当序列被 连续函数代替时,求和自然转化为积分。
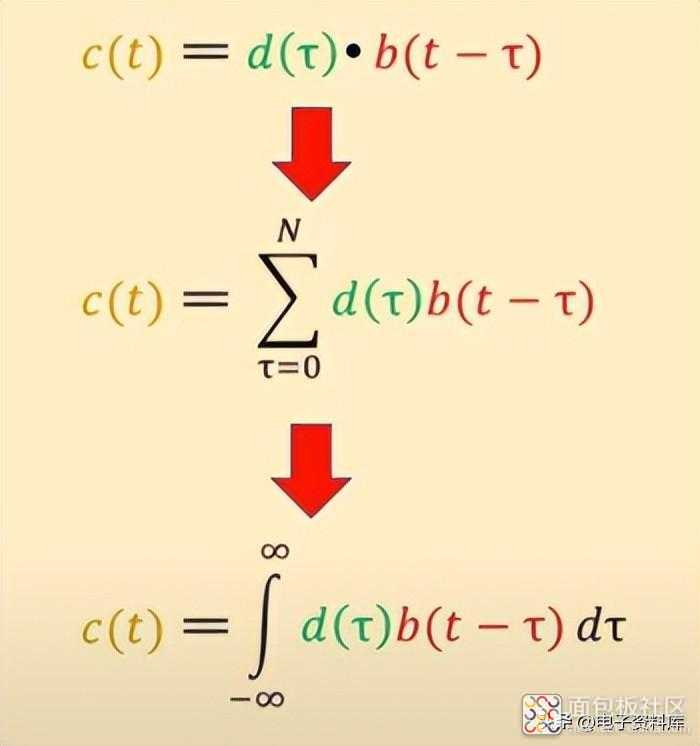
奇怪的疑问
看着上图,在求和到积分的过程中,我产生了一个奇怪的数学疑惑,一个从来没有勇气表达出来的疑惑;毕竟,作者不是数学家,而是工程师。要点如下。当我们从求和到积分时,我们将函数乘以它的微分:因此我们“添加”了一个乘法项。然而,通过将积分应用于物理情况,每一项都有自己的量纲(米、秒、伏特……),因此量纲计数不会相加,并且会出现差异。但并不总是想到要整合的功能,当应用于物理学时,必须是“密度”类型,
如果我们考虑将总和的每一项隐式乘以 1(即“一天”),则差异将得到解决,因为“密度”是“饼干数量/天”。如果你想用积分来写所有东西,那么单个值而不仅仅是函数可以写在积分符号下,通过将它们乘以 delta ...
电气系统LTI 系统的传递函数 ,尤其是那些涉及电气系统(但不仅限于)的传递函数不是在时域中给出,而是 在复频域中给出 s = σ +jω = s +j2πf 即 h(t) 被拉普拉斯变换为H(s),就像 x(t) 和 y(t) 变成 X(s) 和 Y(s) 一样。值得注意的事实是 Y(s) = X(s)H(s),很容易证明。通过这种方式,我们从卷积传递到乘积,可怜的工程师的计算变得容易得多,特别是考虑到进一步简化来自 dB 的使用。
然而,为了更好地理解时域中发生的情况,让我们看看 y(t) 发生了什么,即时域中的输出。
在电气工程和电信中,我们对处理电能的系统感兴趣,这些电能在输入端提供,存储在电容器和电感器中,如果不在系统内消耗,几乎总是一点一点地“呈现”在输出端,有一定的延迟,这一特性自然取决于系统本身的组成。
正是这种记忆在输出中产生了“拖网”,要考虑到这一点,有必要使用 卷积。
系统是 LTI 的事实保证了无论输入函数是什么我们都能够预测输出函数,只要我们知道传递函数 h(t)。
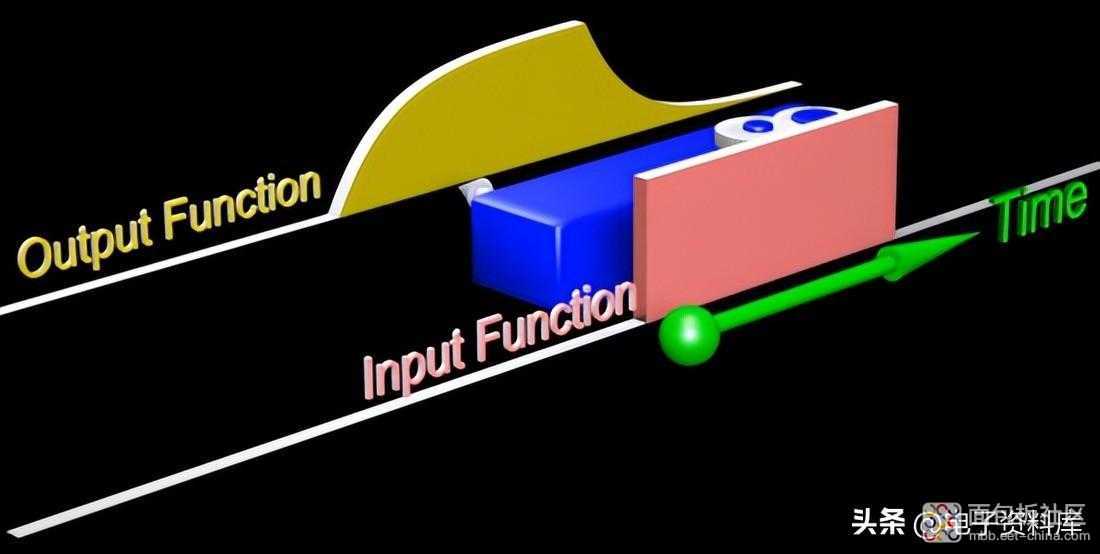
为了找到脉冲响应,我们将脉冲定义为 单位面积的矩形信号,其中矩形的高度在电气情况下对应于电压或电流,而底部是时间间隔 Δt ,在函数的情况下输入继续,成为无穷小 dt。
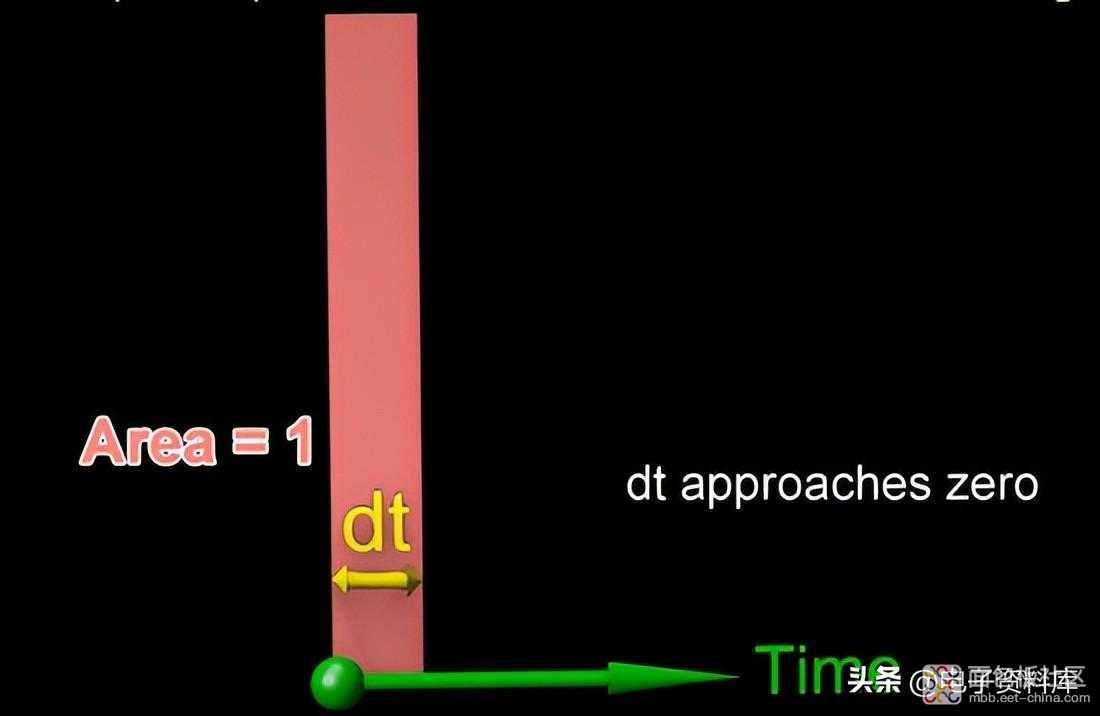
这样一个 无穷小的脉冲由δ(t)表示 ,其对向区域从 -∞ 到 +∞ 积分为 = 1(δ(t) 不是一个正确的函数,但在积分中它表现得好像它是)。
要计算对任何输入函数 x(t) 的响应,诀窍是首先将 x (t) 视为间隔为 dt 的许多连续脉冲的总和,每个单位面积乘以 x(t) 的值每一点。
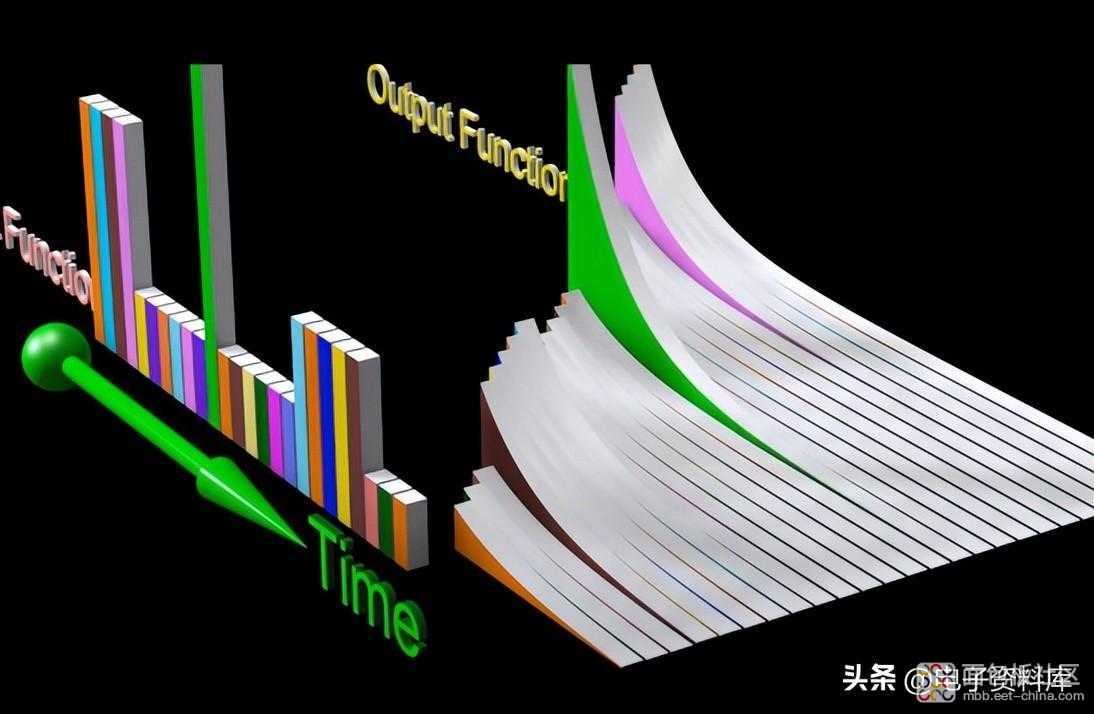
每个脉冲都会产生一个 时间响应 (在阻尼指数类型的图中,例如通过 RC 的电流)h(t),它加起来与其他脉冲的响应相加。随着时间的流逝,要添加的答案会增加:在每个连续的时刻,新答案的开始会增加总和(以代数方式)。也就是说,在每个新的时刻,必须添加所有先前的答案,因此 函数 h(t) 的水平反转,这在前面的图中尚未显示。同样,y(t) 未显示为连续脉冲响应的总和,而是以图形方式交错显示以便更清晰。
输出y(t) 结果是 x(t) 与 h(t) 的卷积。
为了更好地理解它,我现在使用对我来说似乎足够清楚的解释(参见: http ://www.iaincollings.com )。
卷积的三角洲我们从输入 = δ(t) 和指数 h(t) 之间的卷积开始。δ(t) 在时刻 t = 4 时用放置在时间轴上的垂直箭头以图形方式表示,以固定想法。
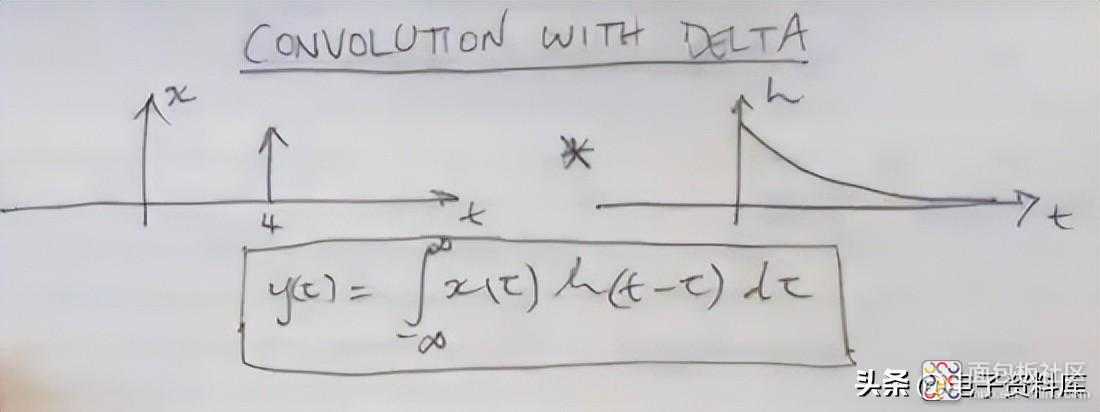
为方便起见,作者对变量进行了两次更改:δ(t) 变为 δ(τ),h(t) 变为 h(α)。不管怎样,他说,它们只是即使在变量发生变化时也能保持其形状的函数。
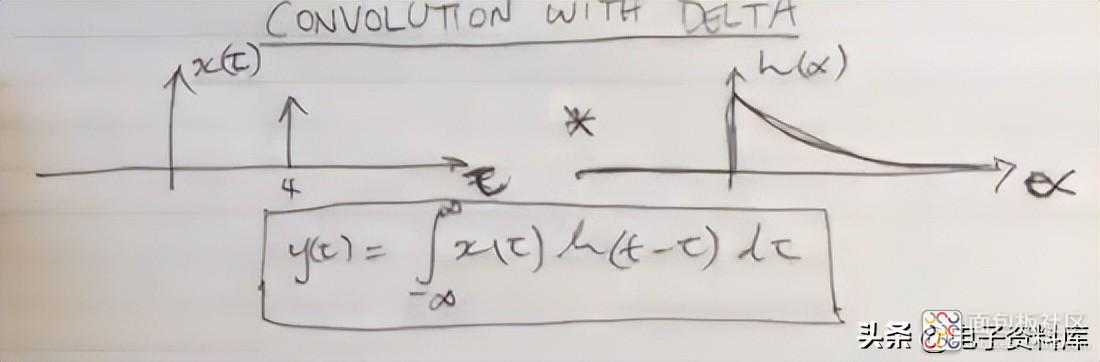
现在他必须在积分下绘制两个函数的乘积,他通过在公式下追踪其他轴来实现:他询问 τ 的哪个值对应于 h(0),他回答说 h(t-τ)该值出现在 t -τ = 0 时,即 -τ = t,然后在垂直轴左侧的 τ 轴上绘制 h(0) 值,因为 τ 为负。
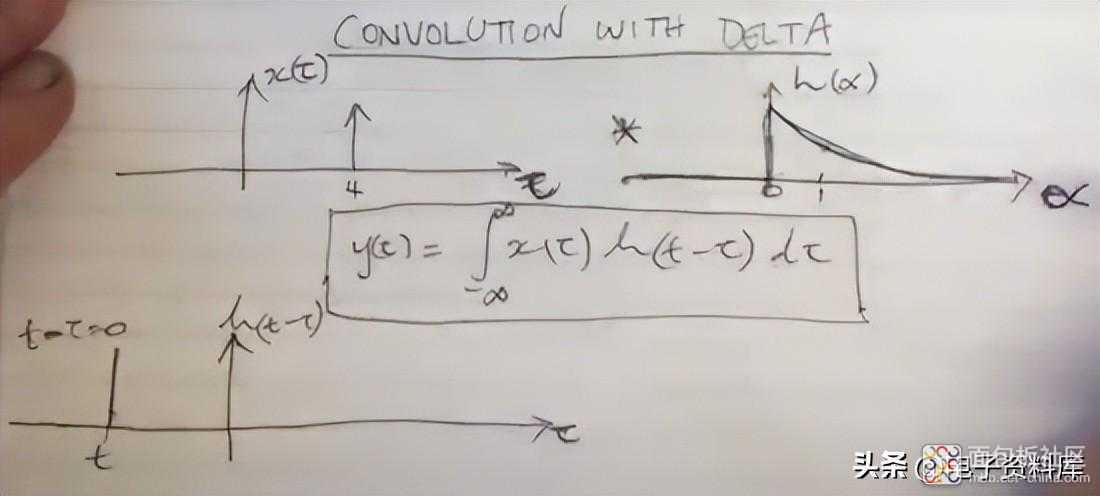
然后他继续确定值 h(1),对于 t-τ=1,即 -τ= t+1,必须将其置于 tau 轴上,因此可以倒转绘制 h(-τ)。
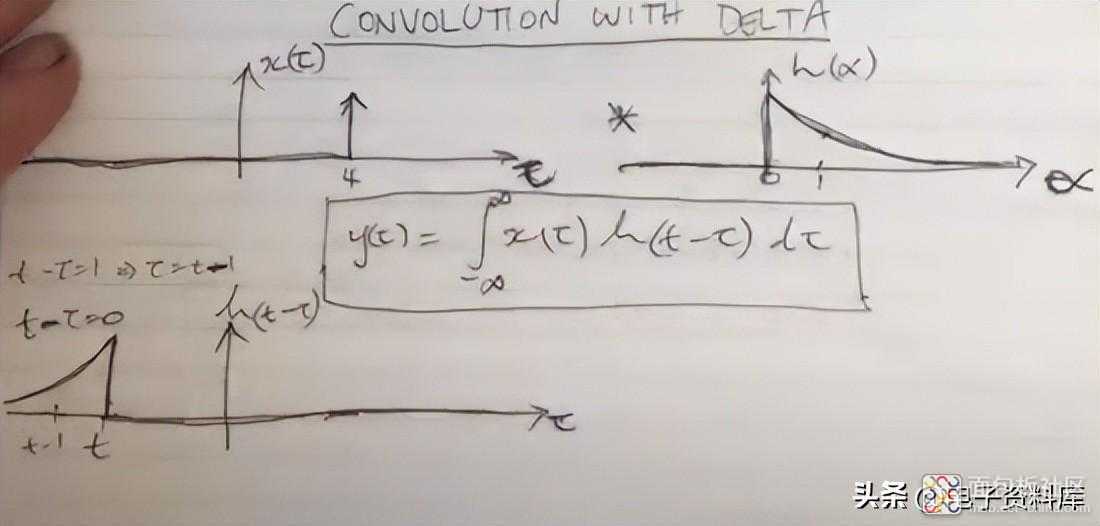
此时他可以画出 y(t)。首先绘制h(t-τ)的图形,定位为t-τ=0即τ=4,其中h(t-τ)= h(0)。随着 τ 的增加,图形向右移动。x(t) 是以 t=4 为中心的 δ(t),即 δ(t-4),因此对于 t=4,乘积 x(t)h(t-τ) 的积分为 h(0 ) 。随着 t 的增加,h(t-τ) 的值减小,因此乘积积分 x(t)h(t-τ) 也减小。最终, delta(tk) 与函数 h(t) 的卷积 产生 h(t) 的右移,变为 h(tk)。
现在我们可以仔细看看 两个连续函数的卷积。
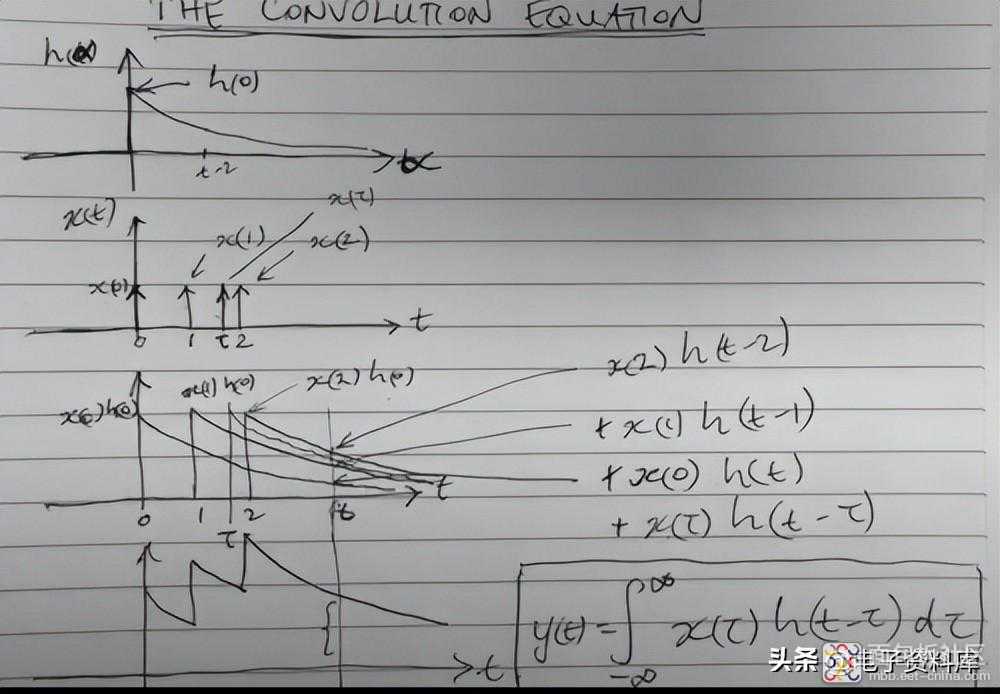
举个例子,其中x(t)由三个delta组成:δ(t)、δ(t-1)、δ(t-2),其中h(t)是图中的指数。作者把这三个δ(t)写成x(0),x(1),x(2)。第三张图表示 t 变化时三个乘积 x(t)h(t) 的总和。
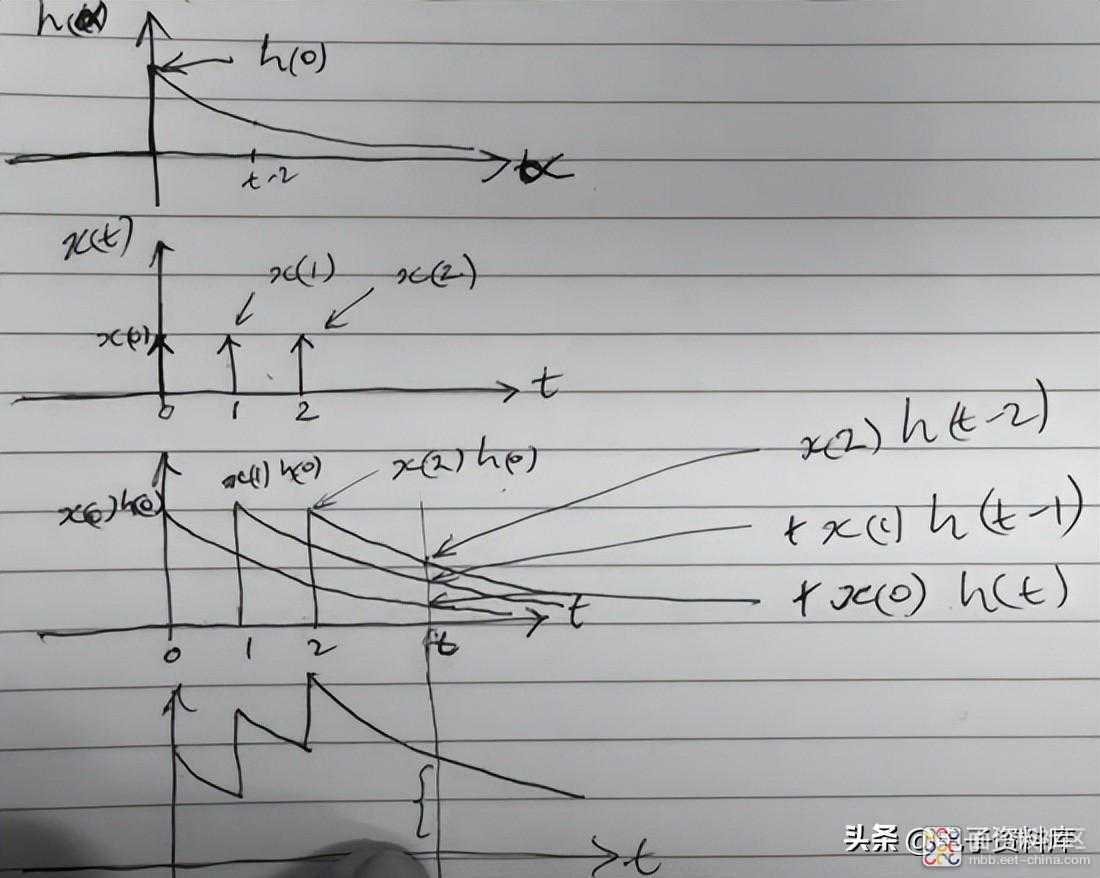
对于 t 的通用值,总和为 x(2)h(t-2) + x(1)h(t-1) + x(0)h(t)。
如果我们对从时刻 τ 开始的三个 δ(t) 添加四分之一,即 δ(t-τ),则乘积 x(τ)h(t-τ) 将添加到前三个乘积的总和中。

如果 x(t) 是一般的连续函数,它可以被认为是无限单位脉冲的总和,在积分符号下,变为 δ(t),表示为 δ(t-τ),其中 τ 建立向右δ(t) 的偏移。
无限数之和δ(t)可以用图中的积分表示,无非是连续函数的卷积公式。
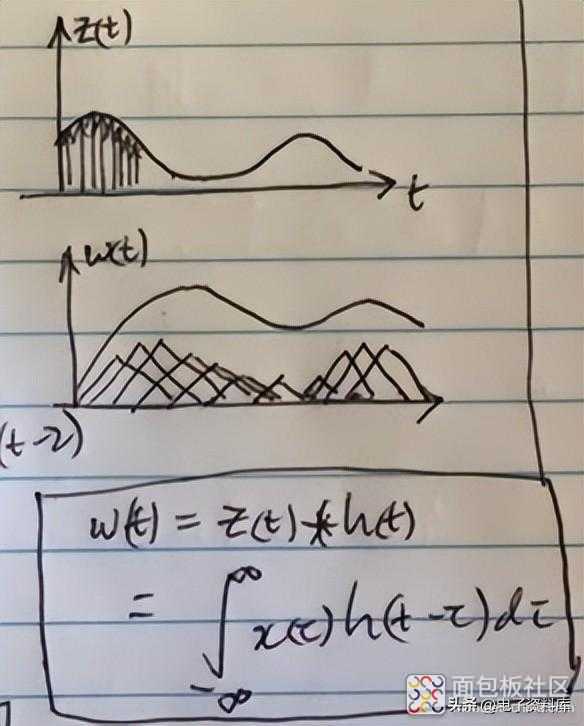
作为上文的进一步说明,下图显示了一个通用函数 x(t) 被认为是无穷大 δ(t) 之和与具有三角形形状的 h(t) 之间的卷积示例。
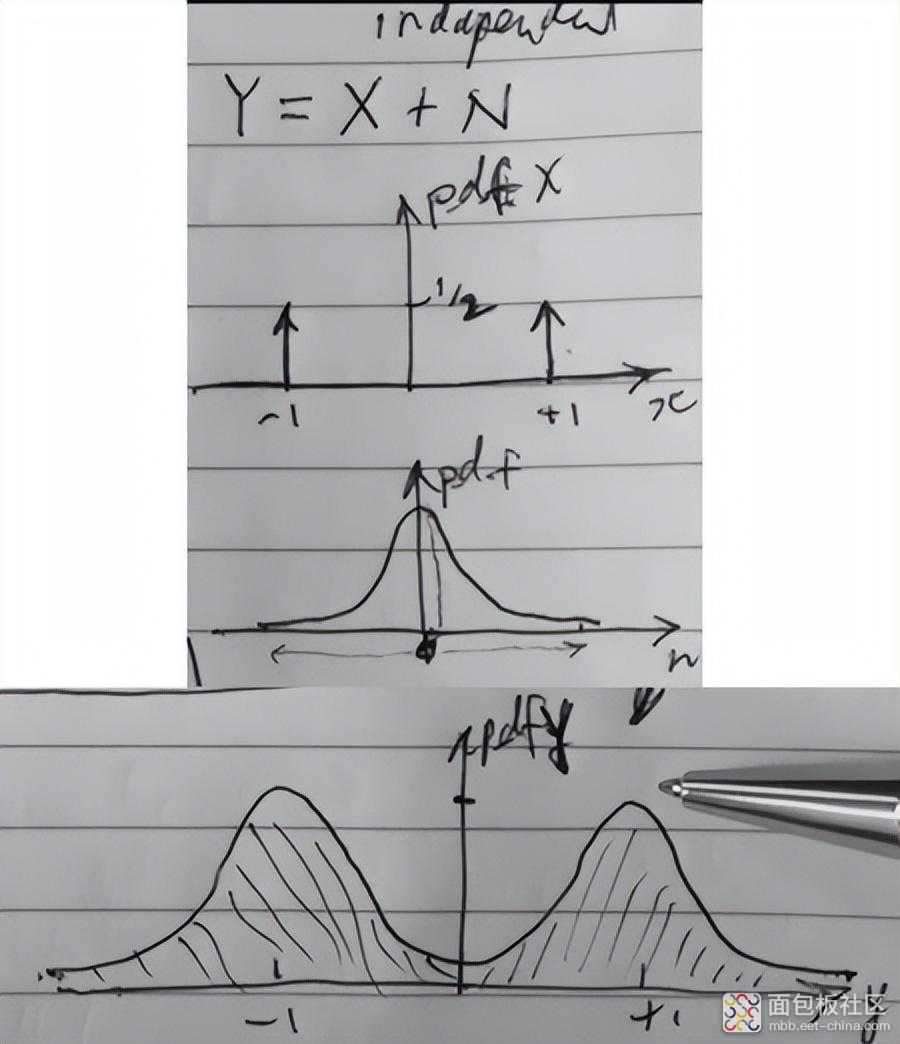
最后, 让我们回到两个统计上独立的随机变量之和的概率密度 (pdf = Probability Density Function),这在之前关于卷积的文章中提到了掷两个骰子。
通信系统的典型 pdf 是Y = X + N ,即 信号x(t) + 高斯噪声n(t),它们在信道中相加并且在统计上是独立的。因此,信号和噪声的和 y(t) 是两个函数的卷积:
y(t) = x(t)*y(t)。
结论
我试图以一种简单、“可见”的方式来说明卷积的概念。如果我没有成功,我邀请读者在评论中向我提问,我会尽一切努力回答。当然,关于它的特性和应用还有很多话要说。例如,已经提到两个函数 f*g 的卷积结果 = L(f)L(g) = F(f)F(g) 即拉普拉斯和傅里叶的两个变换的乘积,整个论述关于卷积和变换之间的联系,特别是 FFT,我们不能在这里做,我们可能会参考后续文章。
来源:电子资料库







 /1
/1 

